|
Здравствуйте! 4 июня я записалась на курс Прикладная статистика. Заплатила за получение сертификата. Изучала лекции, прошла Тест 1. Сегодня вижу, что я вне курса! Почему так произошло? |
Основы вероятностно-статистических методов описания неопределенностей
2.5. Основные проблемы прикладной статистики - описание данных, оценивание и проверка гипотез
Выделяют три основные области статистических методов обработки результатов наблюдений - описание данных, оценивание (характеристик и параметров распределений, регрессионных зависимостей и др.) и проверка статистических гипотез. Рассмотрим основные понятия, применяемые в этих областях.
Основные понятия, используемые при описании данных. Описание данных - предварительный этап статистической обработки. Используемые при описании данных величины применяются при дальнейших этапах статистического анализа - оценивании и проверке гипотез, а также при решении иных задач, возникающих при применении вероятностно-статистических методов принятия решений, например, при статистическом контроле качества продукции и статистическом регулировании технологических процессов.
Статистические данные - это результаты наблюдений (измерений, испытаний, опытов, анализов). Функции результатов наблюдений, используемые, в частности, для оценки параметров распределений и (или) для проверки статистических гипотез, называют "статистиками". (Для математиков надо добавить, что речь идет об измеримых функциях.) Если в вероятностной модели результаты наблюдений рассматриваются как случайные величины (или случайные элементы), то статистики, как функции случайных величин (элементов), сами являются случайными величинами (элементами). Статистики, являющиеся выборочными аналогами характеристик случайных величин (математического ожидания, медианы, дисперсии, моментов и др.) и используемые для оценивания этих характеристик, называют статистическими характеристиками.
Основополагающее понятие в вероятностно-статистических методах принятия решений - выборка. Как уже говорилось, выборка - это: 1) набор наблюдаемых значений или 2) множество объектов, отобранных из изучаемой совокупности. Например, единицы продукции, отобранные из контролируемой партии или потока продукции для контроля и принятия решений. Наблюдаемые значения обозначим 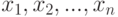 , где
, где  - объем выборки, т.е. число наблюдаемых значений, составляющих выборку. О втором виде выборок уже шла речь при рассмотрении гипергеометрического распределения, когда под выборкой понимался набор единиц продукции, отобранных из партии. Там же обсуждалась вероятностная модель случайной выборки.
- объем выборки, т.е. число наблюдаемых значений, составляющих выборку. О втором виде выборок уже шла речь при рассмотрении гипергеометрического распределения, когда под выборкой понимался набор единиц продукции, отобранных из партии. Там же обсуждалась вероятностная модель случайной выборки.
В вероятностной модели выборки первого вида наблюдаемые значения обычно рассматривают как реализацию независимых одинаково распределенных случайных величин 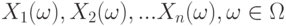 . При этом считают, что полученные при наблюдениях конкретные значения
. При этом считают, что полученные при наблюдениях конкретные значения 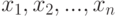 соответствуют определенному элементарному событию
соответствуют определенному элементарному событию 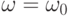 , т.е.
, т.е.

При повторных наблюдениях будут получены иные наблюдаемые значения, соответствующие другому элементарному событию 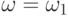 . Цель обработки статистических данных состоит в том, чтобы по результатам наблюдений, соответствующим элементарному событию
. Цель обработки статистических данных состоит в том, чтобы по результатам наблюдений, соответствующим элементарному событию 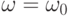 , сделать выводы о вероятностной мере
, сделать выводы о вероятностной мере  и результатах наблюдений при различных возможных
и результатах наблюдений при различных возможных 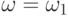 .
.
Применяют и другие, более сложные вероятностные модели выборок. Например, цензурированные выборки соответствуют испытаниям, проводящимся в течение определенного промежутка времени. При этом для части изделий удается замерить время наработки на отказ, а для остальных лишь констатируется, что наработки на отказ для них больше времени испытания. Для выборок второго вида отбор объектов может проводиться в несколько этапов. Например, для входного контроля сигарет могут сначала отбираться коробки, в отобранных коробках - блоки, в выбранных блоках - пачки, а в пачках - сигареты, т.е. существуют четыре ступени отбора. Ясно, что выборка будет обладать иными свойствами, чем простая случайная выборка из совокупности сигарет.
Из приведенного выше определения математической статистики следует, что описание статистических данных дается с помощью частот. Частота - это отношение числа  наблюдаемых единиц, которые принимают заданное значение или лежат в заданном интервале, к общему числу наблюдений
наблюдаемых единиц, которые принимают заданное значение или лежат в заданном интервале, к общему числу наблюдений  , т.е. частота - это
, т.е. частота - это 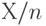 . (В более старой литературе иногда
. (В более старой литературе иногда 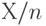 называется относительной частотой, а под частотой имеется в виду
называется относительной частотой, а под частотой имеется в виду  . В старой терминологии можно сказать, что относительная частота - это отношение частоты к общему числу наблюдений.)
. В старой терминологии можно сказать, что относительная частота - это отношение частоты к общему числу наблюдений.)
Отметим, что обсуждаемое определение приспособлено к нуждам одномерной статистики. В случае многомерного статистического анализа, статистики случайных процессов и временных рядов, статистики объектов нечисловой природы нужны несколько иные определения понятия "статистические данные". Не считая нужным давать здесь такие определения, отметим, что в подавляющем большинстве практических постановок исходные статистические данные - это выборка или несколько выборок. А выборка - это конечная совокупность соответствующих математических объектов (чисел, векторов, функций, объектов нечисловой природы).
Число  имеет биномиальное распределение, задаваемое вероятностью
имеет биномиальное распределение, задаваемое вероятностью  того, что случайная величина, с помощью которойp моделируются результаты наблюдений, принимает заданное значение или лежит в заданном интервале, и общим числом наблюдений
того, что случайная величина, с помощью которойp моделируются результаты наблюдений, принимает заданное значение или лежит в заданном интервале, и общим числом наблюдений  . Из закона больших чисел (теорема Бернулли) следует, что
. Из закона больших чисел (теорема Бернулли) следует, что

 (сходимость по вероятности), т.е. частота сходится к вероятности. Теорема Муавра-Лапласа позволяет уточнить скорость сходимости в этом предельном соотношении.
(сходимость по вероятности), т.е. частота сходится к вероятности. Теорема Муавра-Лапласа позволяет уточнить скорость сходимости в этом предельном соотношении.Чтобы от отдельных событий перейти к одновременному рассмотрению многих событий, используют накопленную частоту. Так называется отношение числа единиц, для которых результаты наблюдения меньше заданного значения, к общему числу наблюдений. (Это понятие используется, если результаты наблюдения - действительные числа, а не вектора, функции или объекты нечисловой природы.) Функция, которая выражает зависимость между значениями количественного признака и накопленной частотой, называется эмпирической функцией распределения. Итак, эмпирической функцией распределения 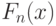 называется доля элементов выборки, меньших
называется доля элементов выборки, меньших  . Эмпирическая функция распределения содержит всю информацию о результатах наблюдений.
. Эмпирическая функция распределения содержит всю информацию о результатах наблюдений.
Чтобы записать выражение для эмпирической функции распределения в виде формулы, введем функцию 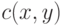 двух переменных:
двух переменных:
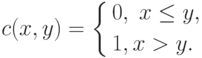
Случайные величины, моделирующие результаты наблюдений, обозначим 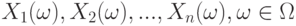 . Тогда эмпирическая функция распределения
. Тогда эмпирическая функция распределения  имеет вид
имеет вид
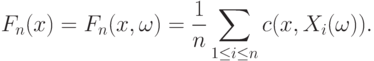
Из закона больших чисел следует, что для каждого действительного числа  эмпирическая функция распределения
эмпирическая функция распределения 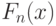 сходится к функции распределения
сходится к функции распределения  результатов наблюдений, т.е.
результатов наблюдений, т.е.
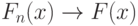 |
( 1) |
 . Советский математик В.И. Гливенко (1897-1940) доказал в 1933 г. более сильное утверждение: сходимость в (1) равномерна по
. Советский математик В.И. Гливенко (1897-1940) доказал в 1933 г. более сильное утверждение: сходимость в (1) равномерна по  , т.е.
, т.е. |
( 2) |
 (сходимость по вероятности).
(сходимость по вероятности).В (2) использовано обозначение 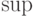 (читается как "супремум"). Для функции
(читается как "супремум"). Для функции  под
под  понимают наименьшее из чисел
понимают наименьшее из чисел  таких, что
таких, что 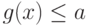 при всех
при всех  . Если функция
. Если функция  достигает максимума в точке
достигает максимума в точке  , то
, то  . В таком случае вместо
. В таком случае вместо 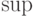 пишут
пишут 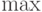 . Хорошо известно, что не все функции достигают максимума.
. Хорошо известно, что не все функции достигают максимума.
В том же 1933 г. А.Н. Колмогоров усилил результат В.И. Гливенко для непрерывных функций распределения  . Рассмотрим случайную величину
. Рассмотрим случайную величину
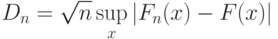
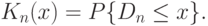
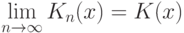
 , где
, где  - так называемая функция распределения Колмогорова.
- так называемая функция распределения Колмогорова.Рассматриваемая работа А.Н. Колмогорова породила одно из основных направлений математической статистики - так называемую непараметрическую статистику. И в настоящее время непараметрические критерии согласия Колмогорова, Смирнова, омега-квадрат широко используются. Они были разработаны для проверки согласия с полностью известным теоретическим распределением, т.е. предназначены для проверки гипотезы 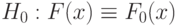 . Основная идея критериев Колмогорова, омега-квадрат и аналогичных им состоит в измерении расстояния между функцией эмпирического распределения и функцией теоретического распределения. Различаются эти критерии видом расстояний в пространстве функций распределения. Аналитические выражения для предельных распределений статистик, расчетные формулы, таблицы распределений и критических значений широко распространены [
[
2.1
]
], поэтому не будем их приводить.
. Основная идея критериев Колмогорова, омега-квадрат и аналогичных им состоит в измерении расстояния между функцией эмпирического распределения и функцией теоретического распределения. Различаются эти критерии видом расстояний в пространстве функций распределения. Аналитические выражения для предельных распределений статистик, расчетные формулы, таблицы распределений и критических значений широко распространены [
[
2.1
]
], поэтому не будем их приводить.
Кроме эмпирической функции распределения, для описания данных используют и другие статистические характеристики. В качестве выборочных средних величин постоянно используют выборочное среднее арифметическое, т.е. сумму значений рассматриваемой величины, полученных по результатам испытания выборки, деленную на ее объем:
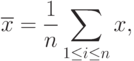
 - объем выборки,
- объем выборки,  - результат измерения (испытания)
- результат измерения (испытания)  -ого элемента выборки.
-ого элемента выборки.Другой вид выборочного среднего - выборочная медиана. Она определяется через порядковые статистики.
Порядковые статистики - это члены вариационного ряда, который получается, если элементы выборки 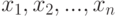 расположить в порядке неубывания:
расположить в порядке неубывания:

Пример 1. Для выборки 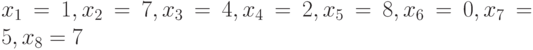 вариационный ряд имеет вид
вариационный ряд имеет вид 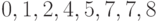 , т.е.
, т.е.  .
.
В вариационном ряду элемент 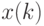 называется
называется  -й порядковой статистикой. Порядковые статистики и функции от них широко используются в вероятностно-статистических методах принятия решений, в эконометрике и в других прикладных областях [
[
2.16
]
].
-й порядковой статистикой. Порядковые статистики и функции от них широко используются в вероятностно-статистических методах принятия решений, в эконометрике и в других прикладных областях [
[
2.16
]
].
Выборочная медиана 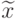 - результат наблюдения, занимающий центральное место в вариационном ряду, построенном по выборке с нечетным числом элементов, или полусумма двух результатов наблюдений, занимающих два центральных места в вариационном ряду, построенном по выборке с четным числом элементов. Таким образом, если объем выборки
- результат наблюдения, занимающий центральное место в вариационном ряду, построенном по выборке с нечетным числом элементов, или полусумма двух результатов наблюдений, занимающих два центральных места в вариационном ряду, построенном по выборке с четным числом элементов. Таким образом, если объем выборки  - нечетное число,
- нечетное число,  , то медиана
, то медиана 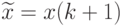 , если же
, если же  - четное число,
- четное число, 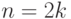 , то медиана
, то медиана ![\widetilde{x}=[x(k) + x(k+1)]/2](/sites/default/files/tex_cache/22ef9d909a5bd6983617ba494f8dc34e.png) , где
, где 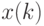 и
и 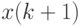 - порядковые статистики.
- порядковые статистики.
В качестве выборочных показателей рассеивания результатов наблюдений чаще всего используют выборочную дисперсию, выборочное среднее квадратическое отклонение и размах выборки.
Согласно [
[
2.1
]
] выборочная дисперсия 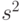 - это сумма квадратов отклонений выборочных результатов наблюдений от их среднего арифметического, деленная на объем выборки:
- это сумма квадратов отклонений выборочных результатов наблюдений от их среднего арифметического, деленная на объем выборки:
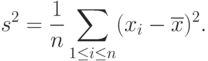
Выборочное среднее квадратическое отклонение  - неотрицательный квадратный корень из дисперсии, т.е.
- неотрицательный квадратный корень из дисперсии, т.е. 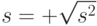 .
.
В некоторых литературных источниках выборочной дисперсией называют другую величину:
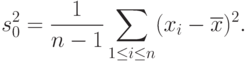
Она отличается от 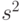 постоянным множителем:
постоянным множителем:
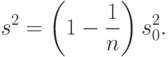
Соответственно выборочным средним квадратическим отклонением в этих литературных источниках называют величину 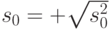 . Тогда очевидно, что
. Тогда очевидно, что
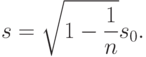
Различие в определениях приводит к различию в алгоритмах расчетов, правилах принятия решений и соответствующих таблицах. Поэтому при использовании тех или иных нормативно-технических и инструктивно-методических материалов, программных продуктов, таблиц необходимо обращать внимание на способ определения выборочных характеристик.
Выбор 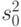 , а не
, а не 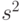 , объясняется тем, что
, объясняется тем, что
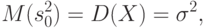
 - случайная величина, имеющая такое же распределение, как и результаты наблюдений. В терминах теории статистического оценивания это означает, что
- случайная величина, имеющая такое же распределение, как и результаты наблюдений. В терминах теории статистического оценивания это означает, что 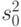 - несмещенная оценка дисперсии (см. ниже). В то же время статистика
- несмещенная оценка дисперсии (см. ниже). В то же время статистика 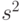 не является несмещенной оценкой дисперсии результатов наблюдений, поскольку
не является несмещенной оценкой дисперсии результатов наблюдений, поскольку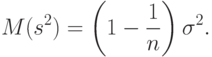
Однако у 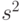 есть другое свойство, оправдывающее использование этой статистики в качестве выборочного показателя рассеивания. Для известных результатов наблюдений
есть другое свойство, оправдывающее использование этой статистики в качестве выборочного показателя рассеивания. Для известных результатов наблюдений 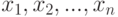 рассмотрим случайную величину
рассмотрим случайную величину  с распределением вероятностей
с распределением вероятностей
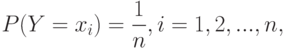
 для всех прочих
для всех прочих  . Это распределение вероятностей называется эмпирическим. Тогда функция распределения
. Это распределение вероятностей называется эмпирическим. Тогда функция распределения  - это эмпирическая функция распределения, построенная по результатам наблюдений
- это эмпирическая функция распределения, построенная по результатам наблюдений 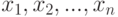 . Вычислим математическое ожидание и дисперсию случайной величины
. Вычислим математическое ожидание и дисперсию случайной величины  :
: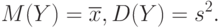
Второе из этих равенств и является основанием для использования 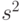 в качестве выборочного показателя рассеивания.
в качестве выборочного показателя рассеивания.
Отметим, что математические ожидания выборочных средних квадратических отклонений 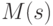 и
и 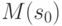 , вообще говоря, не равняются теоретическому среднему квадратическому отклонению
, вообще говоря, не равняются теоретическому среднему квадратическому отклонению  . Например, если
. Например, если  имеет нормальное распределение, объем выборки
имеет нормальное распределение, объем выборки 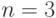 , то
, то
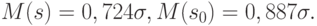
Кроме перечисленных выше статистических характеристик, в качестве выборочного показателя рассеивания используют размах  - разность между
- разность между  -й и первой порядковыми статистиками в выборке объема
-й и первой порядковыми статистиками в выборке объема  , т.е. разность между наибольшим и наименьшим значениями в выборке:
, т.е. разность между наибольшим и наименьшим значениями в выборке: 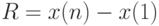 .
.
В ряде вероятностно-статистических методов принятия решений применяют и иные показатели рассеивания. В частности, в методах статистического регулирования процессов используют средний размах - среднее арифметическое размахов, полученных в определенном количестве выборок одинакового объема. Популярно и межквартильное расстояние, т.е. расстояние между выборочными квартилями ![x([0,75n])](/sites/default/files/tex_cache/4308bf34854707316df59d28f54c47d2.png) и
и ![x([0,25n])](/sites/default/files/tex_cache/dbfe1ea1f5ece019e324f34bb42297c6.png) порядка 0,75 и 0,25 соответственно, где
порядка 0,75 и 0,25 соответственно, где ![[0,75n]](/sites/default/files/tex_cache/d3b6778015066d927999b5beea595ea2.png) - целая часть числа
- целая часть числа  , а
, а ![[0,25n]](/sites/default/files/tex_cache/3c857b0f39d6dd2d45394e72e37f08a4.png) -целая часть числа
-целая часть числа  .
.
Основные понятия, используемые при оценивании. Оценивание - это определение приближенного значения неизвестной характеристики или параметра распределения (генеральной совокупности), иной оцениваемой составляющей математической модели реального (экономического, технического и др.) явления или процесса по результатам наблюдений. Иногда формулируют более коротко: оценивание - это определение приближенного значения неизвестного параметра генеральной совокупности по результатам наблюдений. При этом параметром генеральной совокупности может быть либо число, либо набор чисел (вектор), либо функция, либо множество или иной объект нечисловой природы. Например, по результатам наблюдений, распределенных согласно биномиальному закону, оценивают число - параметр  (вероятность успеха).
По результатам наблюдений, имеющих гамма-распределение, оценивают набор из трех чисел - параметры формы
(вероятность успеха).
По результатам наблюдений, имеющих гамма-распределение, оценивают набор из трех чисел - параметры формы  , масштаба
, масштаба  и сдвига
и сдвига  . Способ оценивания функции распределения приведен в теоремах В.И. Гливенко и А.Н. Колмогорова. Оценивают также плотности вероятности, функции, выражающие зависимости между переменными, включенными в вероятностные модели экономических, управленческих или технологических процессов, и т.д. Целью оценивания может быть нахождение упорядочения инвестиционных проектов по экономической эффективности или технических изделий (объектов) по качеству, формулировка правил технической или медицинской диагностики и т.д. (Упорядочения в математической статистике называют также ранжировками. Это - один из видов объектов нечисловой природы.)
. Способ оценивания функции распределения приведен в теоремах В.И. Гливенко и А.Н. Колмогорова. Оценивают также плотности вероятности, функции, выражающие зависимости между переменными, включенными в вероятностные модели экономических, управленческих или технологических процессов, и т.д. Целью оценивания может быть нахождение упорядочения инвестиционных проектов по экономической эффективности или технических изделий (объектов) по качеству, формулировка правил технической или медицинской диагностики и т.д. (Упорядочения в математической статистике называют также ранжировками. Это - один из видов объектов нечисловой природы.)
Оценивание проводят с помощью оценок - статистик, являющихся основой для оценивания неизвестного параметра распределения. В ряде литературных источников термин "оценка" встречается в качестве синонима термина "оценивание". Употреблять одно и то же слово для обозначения двух разных понятий нецелесообразно: оценивание - это действие, а оценка - статистика (функция от результатов наблюдений), используемая в процессе указанного действия или являющаяся его результатом.
Существуют два вида оценивания - точечное и с помощью доверительной области.
Точечное - способ оценивания, заключающийся в том, что значение оценки принимается как неизвестное значение параметра распределения.
Пример 2. Пусть результаты наблюдений 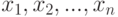 рассматривают в вероятностной модели как случайную выборку из нормального распределения
рассматривают в вероятностной модели как случайную выборку из нормального распределения 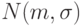 . То есть считают, что результаты наблюдений моделируются как реализации
. То есть считают, что результаты наблюдений моделируются как реализации  независимых одинаково распределенных случайных величин, имеющих функцию нормального распределения
независимых одинаково распределенных случайных величин, имеющих функцию нормального распределения 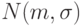 с некоторыми математическим ожиданием
с некоторыми математическим ожиданием  и средним квадратическим отклонением
и средним квадратическим отклонением  , неизвестными статистику. Требуется оценить параметры
, неизвестными статистику. Требуется оценить параметры  и
и  (или
(или  ) по результатам наблюдений. Оценки обозначим
) по результатам наблюдений. Оценки обозначим 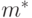 и
и  соответственно.
Обычно в качестве оценки
соответственно.
Обычно в качестве оценки 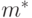 математического ожидания
математического ожидания  используют выборочное среднее арифметическое
используют выборочное среднее арифметическое  , а в качестве оценки
, а в качестве оценки  дисперсии
дисперсии  используют выборочную дисперсию
используют выборочную дисперсию 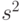 , т.е.
, т.е.

Для оценивания математического ожидания  могут использоваться и другие статистики, например, выборочная медиана
могут использоваться и другие статистики, например, выборочная медиана 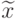 , полусумма минимального и максимального членов вариационного ряда
, полусумма минимального и максимального членов вариационного ряда
![m^{**}=[x(1)+x(n)]/2](/sites/default/files/tex_cache/3053a2a8f9b72c5f6bb1bc37e1d9dee9.png)
 также имеется ряд оценок, в частности,
также имеется ряд оценок, в частности, 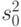 (см. выше) и оценка, основанная на размахе
(см. выше) и оценка, основанная на размахе  , имеющая вид
, имеющая вид![(\sigma^2)^{**}=[a(n)R]^2,](/sites/default/files/tex_cache/9688528f045e0cc236498ecfbd1d013a.png)
 берут из специальных таблиц [
[
2.1
]
]. Эти коэффициенты подобраны так, чтобы для выборок из нормального распределения
берут из специальных таблиц [
[
2.1
]
]. Эти коэффициенты подобраны так, чтобы для выборок из нормального распределения![M[a(n)R]=\sigma.](/sites/default/files/tex_cache/8d86c2097b04c69cc3ceac7ee214ab11.png)
Наличие нескольких методов оценивания одних и тех же параметров приводит к необходимости выбора между этими методами.
Как сравнивать методы оценивания между собой? Сравнение проводят на основе таких показателей качества методов оценивания, как состоятельность, несмещенность, эффективность и др.
Рассмотрим оценку 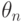 числового параметра
числового параметра  , определенную при
, определенную при 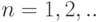 . Оценка
. Оценка 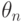 называется состоятельной, если она сходится по вероятности к значению оцениваемого параметра
называется состоятельной, если она сходится по вероятности к значению оцениваемого параметра  при безграничном возрастании объема выборки. Выразим сказанное более подробно. Статистика
при безграничном возрастании объема выборки. Выразим сказанное более подробно. Статистика 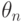 является состоятельной оценкой параметра
является состоятельной оценкой параметра  тогда и только тогда, когда для любого положительного числа
тогда и только тогда, когда для любого положительного числа  справедливо предельное соотношение
справедливо предельное соотношение
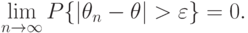
Пример 3. Из закона больших чисел следует, что  является состоятельной оценкой
является состоятельной оценкой  (в приведенной выше теореме Чебышева предполагалось существование дисперсии
(в приведенной выше теореме Чебышева предполагалось существование дисперсии 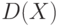 ; однако, как доказал А.Я. Хинчин [
[
2.3
]
], достаточно выполнения более слабого условия - существования математического ожидания
; однако, как доказал А.Я. Хинчин [
[
2.3
]
], достаточно выполнения более слабого условия - существования математического ожидания 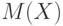 ).
).
Пример 4. Все указанные выше оценки параметров нормального распределения являются состоятельными.
Вообще все (за редчайшими исключениями) оценки параметров, используемые в вероятностно-статистических методах принятия решений, являются состоятельными.
Пример 5. Так, согласно теореме В.И. Гливенко, эмпирическая функция распределения  является состоятельной оценкой функции распределения результатов наблюдений
является состоятельной оценкой функции распределения результатов наблюдений  .
.
При разработке новых методов оценивания следует в первую очередь проверять состоятельность предлагаемых методов.
Второе важное свойство оценок - несмещенность. Несмещенная оценка 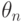 - это оценка параметра
- это оценка параметра  , математическое ожидание которой равно значению оцениваемого параметра:
, математическое ожидание которой равно значению оцениваемого параметра:  .
.
Пример 6. Из приведенных выше результатов следует, что  и
и 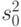 являются несмещенными оценками параметров
являются несмещенными оценками параметров  и
и  нормального распределения. Поскольку
нормального распределения. Поскольку 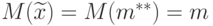 , то выборочная медиана
, то выборочная медиана 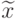 и полусумма крайних членов вариационного ряда
и полусумма крайних членов вариационного ряда 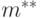 - также несмещенные оценки математического ожидания
- также несмещенные оценки математического ожидания  нормального распределения. Однако
нормального распределения. Однако
![M(s^2)\ne\sigma^2, M[(\sigma^2)^{**}]\ne\sigma^2,](/sites/default/files/tex_cache/8cd63527d2d448264cdcf37bb0ba526d.png)
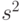 и
и  не являются состоятельными оценками дисперсии
не являются состоятельными оценками дисперсии  нормального распределения.
нормального распределения.Оценки, для которых соотношение  неверно, называются смещенными. При этом разность между математическим ожиданием оценки
неверно, называются смещенными. При этом разность между математическим ожиданием оценки 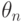 и оцениваемым параметром
и оцениваемым параметром  , т.е.
, т.е. 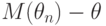 , называется смещением оценки.
, называется смещением оценки.
Пример 7. Для оценки 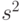 , как следует из сказанного выше, смещение равно
, как следует из сказанного выше, смещение равно

Смещение оценки 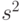 стремится к 0 при
стремится к 0 при  .
.
Оценка, для которой смещение стремится к 0, когда объем выборки стремится к бесконечности, называется асимптотически несмещенной. В примере 7 показано, что оценка 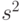 является асимптотически несмещенной.
является асимптотически несмещенной.
Практически все оценки параметров, используемые в вероятностно-статистических методах принятия решений, являются либо несмещенными, либо асимптотически несмещенными. Для несмещенных оценок показателем точности оценки служит дисперсия - чем дисперсия меньше, тем оценка лучше. Для смещенных оценок показателем точности служит математическое ожидание квадрата оценки 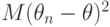 . Как следует из основных свойств математического ожидания и дисперсии,
. Как следует из основных свойств математического ожидания и дисперсии,
![d_n(\theta_n)=M[(\theta_n-\theta)^2]=D(\theta_n)+(M(\theta_n)-\theta)^2,](/sites/default/files/tex_cache/8413885decf40f358fd73ba606112bee.png) |
( 3) |
Для подавляющего большинства оценок параметров, используемых в вероятностно-статистических методах принятия решений, дисперсия имеет порядок 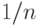 , а смещение - не более чем
, а смещение - не более чем 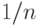 , где
, где  - объем выборки. Для таких оценок при больших
- объем выборки. Для таких оценок при больших  второе слагаемое в правой части (3) пренебрежимо мало по сравнению с первым, и для них справедливо приближенное равенство
второе слагаемое в правой части (3) пренебрежимо мало по сравнению с первым, и для них справедливо приближенное равенство
![d_n(\theta_n)=M[(\theta_n-\theta)^2]\approxD(\theta_n)\approx\frac{c}{n},c=c(\theta_n,\theta),](/sites/default/files/tex_cache/97d3c53f4149c0dfa180a5126779419b.png) |
( 4) |
где  - число, определяемое методом вычисления оценок
- число, определяемое методом вычисления оценок 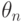 и истинным значением оцениваемого параметра
и истинным значением оцениваемого параметра  .
.
С дисперсией оценки связано третье важное свойство метода оценивания - эффективность. Эффективная оценка - это несмещенная оценка, имеющая наименьшую дисперсию из всех возможных несмещенных оценок данного параметра.
Доказано [
[
2.10
]
], что  и
и 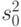 являются эффективными оценками параметров
являются эффективными оценками параметров  и
и  нормального распределения. В то же время для выборочной медианы
нормального распределения. В то же время для выборочной медианы 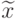 справедливо предельное соотношение
справедливо предельное соотношение
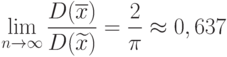
Другими словами, эффективность выборочной медианы, т.е. отношение дисперсии эффективной оценки  параметра
параметра  к дисперсии несмещенной оценки
к дисперсии несмещенной оценки 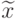 этого параметра при больших
этого параметра при больших  близка к 0,637. Именно из-за сравнительно низкой эффективности выборочной медианы в качестве оценки математического ожидания нормального распределения обычно используют выборочное среднее арифметическое.
близка к 0,637. Именно из-за сравнительно низкой эффективности выборочной медианы в качестве оценки математического ожидания нормального распределения обычно используют выборочное среднее арифметическое.
