|
Здравствуйте! 4 июня я записалась на курс Прикладная статистика. Заплатила за получение сертификата. Изучала лекции, прошла Тест 1. Сегодня вижу, что я вне курса! Почему так произошло? |
Основы вероятностно-статистических методов описания неопределенностей
2.4. Случайные величины и их распределения
Распределения случайных величин и функции распределения. Распределение числовой случайной величины – это функция, которая однозначно определяет вероятность того, что случайная величина принимает заданное значение или принадлежит к некоторому заданному интервалу.
Первое – если случайная величина принимает конечное число значений. Тогда распределение задается функцией 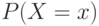 , ставящей в соответствие каждому возможному значению
, ставящей в соответствие каждому возможному значению  случайной величины
случайной величины  вероятность того, что
вероятность того, что 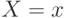 .
.
Второе – если случайная величина принимает бесконечно много значений. Это возможно лишь тогда, когда вероятностное пространство, на котором определена случайная величина, состоит из бесконечного числа элементарных событий. Тогда распределение задается набором вероятностей 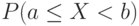 для всех пар чисел
для всех пар чисел  таких, что
таких, что  . Распределение может быть задано с помощью так называемой функции распределения
. Распределение может быть задано с помощью так называемой функции распределения 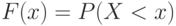 , определяющей для всех действительных х вероятность того, что случайная величина
, определяющей для всех действительных х вероятность того, что случайная величина  принимает значения, меньшие
принимает значения, меньшие  . Ясно, что
. Ясно, что

Это соотношение показывает, что как распределение может быть рассчитано по функции распределения, так и наоборот, функция распределения – по распределению.
Используемые в вероятностно-статистических методах принятия решений и других прикладных исследованиях функции распределения бывают либо дискретными, либо непрерывными, либо их комбинациями.
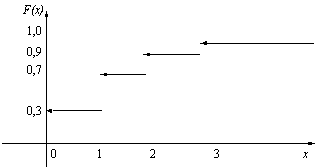
Дискретные функции распределения соответствуют дискретным случайным величинам, принимающим конечное число значений или же значения из множества, элементы которого можно перенумеровать натуральными числами (такие множества в математике называют счетными). Их график имеет вид ступенчатой лестницы ( рис. 2.1).
Пример 1. Число  дефектных изделий в партии принимает значение 0 с вероятностью 0,3, значение 1 – с вероятностью 0,4, значение 2 – с вероятностью 0,2 и значение 3 – с вероятностью 0,1. График функции распределения случайной величины
дефектных изделий в партии принимает значение 0 с вероятностью 0,3, значение 1 – с вероятностью 0,4, значение 2 – с вероятностью 0,2 и значение 3 – с вероятностью 0,1. График функции распределения случайной величины  изображен на
рис.
2.1.
изображен на
рис.
2.1.
Непрерывные функции распределения не имеют скачков. Они монотонно возрастают1В некоторых случаях, например, при изучении цен, объемов выпуска или суммарной наработки на отказ в задачах надежности, функции распределения постоянны на некоторых интервалах, в которые значения исследуемых случайных величин не могут попасть. при увеличении аргумента – от 0 при 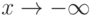 до 1 при
до 1 при 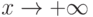 . Случайные величины, имеющие непрерывные функции распределения, называют непрерывными.
. Случайные величины, имеющие непрерывные функции распределения, называют непрерывными.
Непрерывные функции распределения, используемые в вероятностно-статистических методах принятия решений, имеют производные. Первая производная  функции распределения
функции распределения 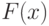 называется плотностью вероятности,
называется плотностью вероятности,
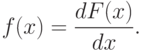
По плотности вероятности можно определить функцию распределения:
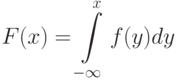
Для любой функции распределения
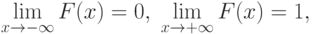
а потому
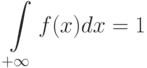
Перечисленные свойства функций распределения постоянно используются в вероятностно-статистических методах принятия решений. В частности, из последнего равенства вытекает конкретный вид констант в формулах для плотностей вероятностей, рассматриваемых ниже.
Пример 2. Часто используется следующая функция распределения:
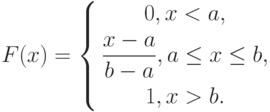 |
( 1) |
где  и
и  – некоторые числа,
– некоторые числа,  . Найдем плотность вероятности этой функции распределения:
. Найдем плотность вероятности этой функции распределения:
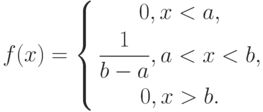
(в точках  и
и  производная функции
производная функции  не существует).
не существует).
Случайная величина с функцией распределения (1) называется "равномерно распределенной на отрезке ![[a; b]](/sites/default/files/tex_cache/65c152d51ed08a1761f5a8cb653eafe5.png) ".
".
Смешанные функции распределения встречаются, в частности, тогда, когда наблюдения в какой-то момент прекращаются. Например, при анализе статистических данных, полученных при использовании планов испытаний на надежность, предусматривающих прекращение испытаний по истечении некоторого срока. Или при анализе данных о технических изделиях, потребовавших гарантийного ремонта.
Пример 3. Пусть, например, срок службы электрической лампочки – случайная величина с функцией распределения 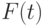 , а испытание проводится до выхода лампочки из строя, если это произойдет менее чем за 100 часов от начала испытаний, или до момента
, а испытание проводится до выхода лампочки из строя, если это произойдет менее чем за 100 часов от начала испытаний, или до момента  = 100 часов. Пусть
= 100 часов. Пусть 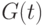 – функция распределения времени эксплуатации лампочки в исправном состоянии при этом испытании. Тогда
– функция распределения времени эксплуатации лампочки в исправном состоянии при этом испытании. Тогда

Функция 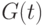 имеет скачок в точке
имеет скачок в точке  , поскольку соответствующая случайная величина принимает значение
, поскольку соответствующая случайная величина принимает значение  с вероятностью
с вероятностью 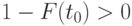 .
.
Характеристики случайных величин. В вероятностно-статистических методах принятия решений используется ряд характеристик случайных величин, выражающихся через функции распределения и плотности вероятностей.
При описании дифференциации доходов, при нахождении доверительных границ для параметров распределений случайных величин и во многих иных случаях используется такое понятие, как "квантиль порядка  ", где
", где 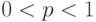 (обозначается
(обозначается 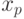 ). Квантиль порядка
). Квантиль порядка  – значение случайной величины, для которого функция распределения принимает значение
– значение случайной величины, для которого функция распределения принимает значение  или имеет место "скачок" со значения меньше
или имеет место "скачок" со значения меньше  до значения больше
до значения больше  (
рис.
2.2). Может случиться, что это условие выполняется для всех значений
(
рис.
2.2). Может случиться, что это условие выполняется для всех значений  , принадлежащих этому интервалу (т.е. функция распределения постоянна на этом интервале и равна
, принадлежащих этому интервалу (т.е. функция распределения постоянна на этом интервале и равна  ). Тогда каждое такое значение называется "квантилью порядка
). Тогда каждое такое значение называется "квантилью порядка  ". Для непрерывных функций распределения, как правило, существует единственная квантиль
". Для непрерывных функций распределения, как правило, существует единственная квантиль 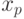 порядка
порядка  (
рис.
2.2), причем
(
рис.
2.2), причем
 |
( 2) |
Пример 4. Найдем квантиль 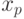 порядка
порядка  для функции распределения
для функции распределения 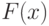 из (1).
из (1).
При 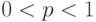 квантиль
квантиль 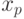 находится из уравнения
находится из уравнения
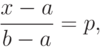
т.е. 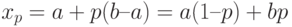 . При
. При  любое
любое  является квантилью порядка
является квантилью порядка  . Квантилью порядка
. Квантилью порядка 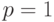 является любое число
является любое число 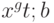 .
.
Для дискретных распределений, как правило, не существует 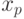 , удовлетворяющих уравнению (2). Точнее, если распределение случайной величины задается табл.2.2, где
, удовлетворяющих уравнению (2). Точнее, если распределение случайной величины задается табл.2.2, где 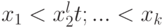 , то равенство (2), рассматриваемое как уравнение относительно
, то равенство (2), рассматриваемое как уравнение относительно 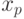 , имеет решения только для
, имеет решения только для  значений
значений  , а именно,
, а именно,
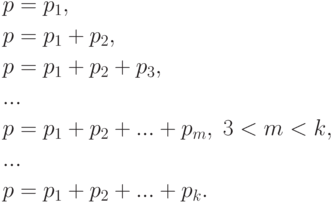
Значения  случайной величины случайной величины 
|
 |
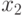 |
... |  |
Вероятности 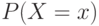
|
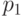 |
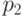 |
... | 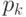 |
Для перечисленных  значений вероятности
значений вероятности  решение
решение 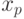 уравнения (2) неединственно, а именно,
уравнения (2) неединственно, а именно,
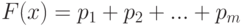
для всех  таких, что
таких, что  . То есть
. То есть 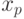 – любое число из интервала
– любое число из интервала ![(x_m; x_m+1]](/sites/default/files/tex_cache/fbd0f166d182a5d5000c4216d283d6d5.png) . Для всех остальных
. Для всех остальных  из промежутка (0;1), не входящих в перечень (3), имеет место "скачок" со значения меньше
из промежутка (0;1), не входящих в перечень (3), имеет место "скачок" со значения меньше  до значения больше
до значения больше  . А именно, если
. А именно, если
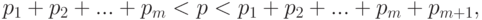
то 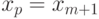 .
.
Рассмотренное свойство дискретных распределений создает значительные трудности при табулировании и использовании подобных распределений, поскольку невозможно точно выдержать типовые численные значения характеристик распределения. В частности, это так для критических значений и уровней значимости непараметрических статистических критериев (см. ниже), поскольку распределения статистик этих критериев дискретны.
Большое значение в статистике имеет квантиль порядка 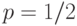 . Он называется медианой (случайной величины
. Он называется медианой (случайной величины  или ее функции распределения
или ее функции распределения  ) и обозначается
) и обозначается  . В геометрии есть понятие "медиана" – прямая, проходящая через вершину треугольника и делящая противоположную его сторону пополам. В математической статистике медиана делит пополам не сторону треугольника, а распределение случайной величины: равенство
. В геометрии есть понятие "медиана" – прямая, проходящая через вершину треугольника и делящая противоположную его сторону пополам. В математической статистике медиана делит пополам не сторону треугольника, а распределение случайной величины: равенство 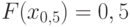 означает, что вероятность попасть левее
означает, что вероятность попасть левее 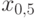 и вероятность попасть правее
и вероятность попасть правее 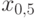 (или непосредственно в
(или непосредственно в 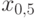 ) равны между собой и равны 1/2, т.е.
) равны между собой и равны 1/2, т.е.
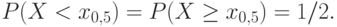
Медиана указывает "центр" распределения. С точки зрения одной из современных концепций – теории устойчивых статистических процедур – медиана является более хорошей характеристикой случайной величины, чем математическое ожидание [ [ 1.15 ] , [ 2.16 ] ]. При обработке результатов измерений в порядковой шкале (см. лекцию о теории измерений) медианой можно пользоваться, а математическим ожиданием – нет.
Ясный смысл имеет такая характеристика случайной величины, как мода – значение (или значения) случайной величины, соответствующее локальному максимуму плотности вероятности для непрерывной случайной величины или локальному максимуму вероятности для дискретной случайной величины.
Если  – мода случайной величины с плотностью
– мода случайной величины с плотностью  , то, как известно из дифференциального исчисления,
, то, как известно из дифференциального исчисления, 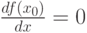 .
.
У случайной величины может быть много мод. Так, для равномерного распределения (1) каждая точка  такая, что
такая, что 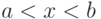 , является модой. Однако это исключение. Большинство случайных величин, используемых в вероятностно-статистических методах принятия решений и других прикладных исследованиях, имеют одну моду. Случайные величины, плотности, распределения, имеющие одну моду, называются унимодальными.
, является модой. Однако это исключение. Большинство случайных величин, используемых в вероятностно-статистических методах принятия решений и других прикладных исследованиях, имеют одну моду. Случайные величины, плотности, распределения, имеющие одну моду, называются унимодальными.
Математическое ожидание для дискретных случайных величин с конечным числом значений рассмотрено в 2.2. Для непрерывной случайной величины  математическое ожидание
математическое ожидание 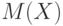 удовлетворяет равенству
удовлетворяет равенству
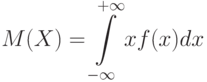
являющемуся аналогом формулы (5) из утверждения 2  2.2.
2.2.
Пример 5. Математическое ожидание для равномерно распределенной случайной величины  равно
равно
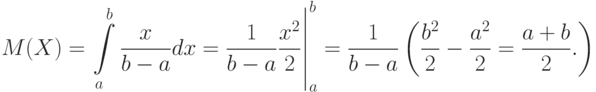
Для рассматриваемых в настоящем параграфе случайных величин верны все те свойства математических ожиданий и дисперсий, которые были рассмотрены ранее в 2.2 для дискретных случайных величин с конечным числом значений. Однако доказательства этих свойств не приводим, поскольку они требуют углубления в математические тонкости, не являющиеся необходимыми для понимания и квалифицированного применения вероятностно-статистических методов принятия решений.
Замечание. В настоящем учебнике сознательно обходятся математические тонкости, связанные, в частности, с понятиями измеримых множеств и измеримых функций,  -алгебры событий и т.п. Желающим освоить эти понятия необходимо обратиться к специальной литературе, в частности, к энциклопедии [
[
2.2
]
].
-алгебры событий и т.п. Желающим освоить эти понятия необходимо обратиться к специальной литературе, в частности, к энциклопедии [
[
2.2
]
].
Каждая из трех характеристик – математическое ожидание, медиана, мода – описывает "центр" распределения вероятностей. Понятие "центр" можно определять разными способами – отсюда три разные характеристики. Однако для важного класса распределений – симметричных унимодальных – все три характеристики совпадают.
Плотность распределения  – плотность симметричного распределения, если найдется число
– плотность симметричного распределения, если найдется число  такое, что
такое, что
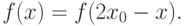 |
( 3) |
Равенство (3) означает, что график функции 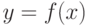 симметричен относительно вертикальной прямой, проходящей через центр симметрии
симметричен относительно вертикальной прямой, проходящей через центр симметрии  . Из (3) следует, что функция симметричного распределения удовлетворяет соотношению
. Из (3) следует, что функция симметричного распределения удовлетворяет соотношению
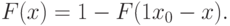 |
( 4) |
Для симметричного распределения с одной модой математическое ожидание, медиана и мода совпадают и равны  .
.
Наиболее важен случай симметрии относительно 0, т.е. 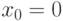 . Тогда (3) и (4) переходят в равенства
. Тогда (3) и (4) переходят в равенства
 |
( 5) |
и
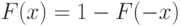 |
( 6) |
соответственно. Приведенные соотношения показывают, что симметричные распределения нет необходимости табулировать при всех  , достаточно иметь таблицы при
, достаточно иметь таблицы при 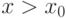 .
.
Отметим еще одно свойство симметричных распределений, постоянно используемое в вероятностно-статистических методах принятия решений и других прикладных исследованиях. Для непрерывной функции распределения
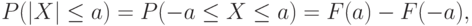
где  – функция распределения случайной величины
– функция распределения случайной величины  . Если функция распределения
. Если функция распределения  симметрична относительно 0, т.е. для нее справедлива формула (6), то
симметрична относительно 0, т.е. для нее справедлива формула (6), то

Часто используют другую формулировку рассматриваемого утверждения: если

Если 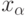 и
и 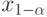 – квантили порядка
– квантили порядка  и
и 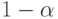 соответственно (см. (2)) функции распределения, симметричной относительно 0, то из (6) следует, что
соответственно (см. (2)) функции распределения, симметричной относительно 0, то из (6) следует, что

От характеристик положения – математического ожидания, медианы, моды – перейдем к характеристикам разброса случайной величины  : дисперсии
: дисперсии 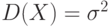 , среднему квадратическому отклонению
, среднему квадратическому отклонению  и коэффициенту вариации
и коэффициенту вариации 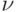 . Определение и свойства дисперсии для дискретных случайных величин рассмотрены в
"Различные виды статистических данных"
. Для непрерывных случайных величин
. Определение и свойства дисперсии для дискретных случайных величин рассмотрены в
"Различные виды статистических данных"
. Для непрерывных случайных величин
![D(X)=M[(X-M(X))^2]=\int\limits_{-\infty}^{+\infty}(x-M(X))^2 f(x)dx.](/sites/default/files/tex_cache/a621dce410482b68ec5a69c3e1fb2517.png)
Среднее квадратическое отклонение – это неотрицательное значение квадратного корня из дисперсии:
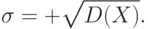
Коэффициент вариации – это отношение среднего квадратического отклонения к математическому ожиданию:
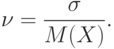
Коэффициент вариации применяется при 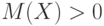 . Он измеряет разброс в относительных единицах, в то время как среднее квадратическое отклонение – в абсолютных.
. Он измеряет разброс в относительных единицах, в то время как среднее квадратическое отклонение – в абсолютных.
Пример 6. Для равномерно распределенной случайной величины Х найдем дисперсию, среднеквадратическое отклонение и коэффициент вариации. Дисперсия равна:
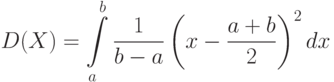
Замена переменной 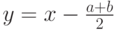 дает возможность записать:
дает возможность записать:
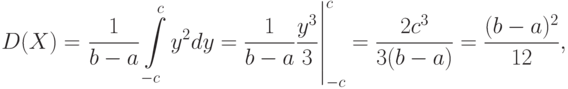
где 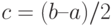 . Следовательно, среднее квадратическое отклонение равно
. Следовательно, среднее квадратическое отклонение равно 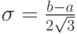 , а коэффициент вариации таков:
, а коэффициент вариации таков:  .
.
По каждой случайной величине  определяют еще три величины – центрированную
определяют еще три величины – центрированную  , нормированную
, нормированную 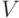 и приведенную
и приведенную 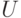 . Центрированная случайная величина
. Центрированная случайная величина  – это разность между данной случайной величиной
– это разность между данной случайной величиной  и ее математическим ожиданием
и ее математическим ожиданием 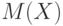 , т.е.
, т.е.  . Математическое ожидание центрированной случайной величины
. Математическое ожидание центрированной случайной величины  равно 0, а дисперсия – дисперсии данной случайной величины:
равно 0, а дисперсия – дисперсии данной случайной величины: 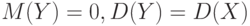 . Функция распределения
. Функция распределения 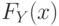 центрированной случайной величины
центрированной случайной величины  связана с функцией распределения
связана с функцией распределения 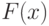 исходной случайной величины
исходной случайной величины  соотношением:
соотношением:
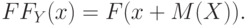
Для плотностей этих случайных величин справедливо равенство
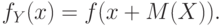
Нормированная случайная величина 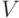 – это отношение данной случайной величины
– это отношение данной случайной величины  к ее среднему квадратическому отклонению
к ее среднему квадратическому отклонению  , т.е.
, т.е. 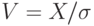 . Математическое ожидание и дисперсия нормированной случайной величины
. Математическое ожидание и дисперсия нормированной случайной величины 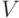 выражаются через характеристики
выражаются через характеристики  так:
так:
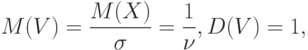
где 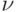 – коэффициент вариации исходной случайной величины
– коэффициент вариации исходной случайной величины  . Для функции распределения
. Для функции распределения 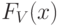 и плотности
и плотности 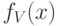 нормированной случайной величины
нормированной случайной величины 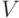 имеем:
имеем:

где 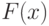 – функция распределения исходной случайной величины
– функция распределения исходной случайной величины  , а
, а  – ее плотность вероятности.
– ее плотность вероятности.
Приведенная случайная величина  – это центрированная и нормированная случайная величина:
– это центрированная и нормированная случайная величина:
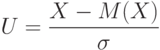
Для приведенной случайной величины
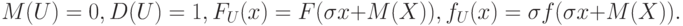 |
( 7) |
Нормированные, центрированные и приведенные случайные величины постоянно используются как в теоретических исследованиях, так и в алгоритмах, программных продуктах, нормативно-технической и инструктивно-методической документации. В частности потому, что равенства 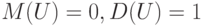 позволяют упростить обоснования методов, формулировки теорем и расчетные формулы.
позволяют упростить обоснования методов, формулировки теорем и расчетные формулы.
Используются преобразования случайных величин и более общего плана. Так, если 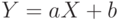 , где
, где  и
и  – некоторые числа, то
– некоторые числа, то
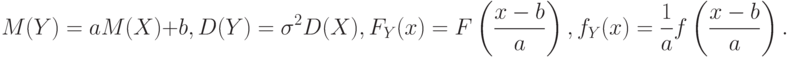 |
( 8) |
Пример 7. Если 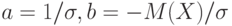 то
то  – приведенная случайная величина, и формулы (8) переходят в формулы (7).
– приведенная случайная величина, и формулы (8) переходят в формулы (7).
С каждой случайной величиной  можно связать множество случайных величин
можно связать множество случайных величин  , заданных формулой
, заданных формулой 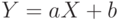 при различных
при различных 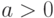 и
и  . Это множество называют масштабно-сдвиговым семейством, порожденным случайной величиной
. Это множество называют масштабно-сдвиговым семейством, порожденным случайной величиной  . Функции распределения
. Функции распределения 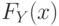 составляют масштабно-сдвиговое семейство распределений, порожденное функцией распределения
составляют масштабно-сдвиговое семейство распределений, порожденное функцией распределения 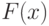 . Вместо
. Вместо 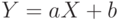 часто используют запись
часто используют запись
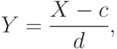 |
( 9) |
где
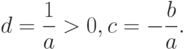
Число  называют параметром сдвига, а число
называют параметром сдвига, а число 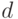 – параметром масштаба. Формула (9) показывает, что
– параметром масштаба. Формула (9) показывает, что  – результат измерения некоторой величины – переходит в
– результат измерения некоторой величины – переходит в  – результат измерения той же величины, если начало измерения перенести в точку
– результат измерения той же величины, если начало измерения перенести в точку  , а затем использовать новую единицу измерения, в
, а затем использовать новую единицу измерения, в 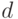 раз большую старой.
раз большую старой.
Для масштабно-сдвигового семейства (9) распределение  называют стандартным. В вероятностно-статистических методах принятия решений и других прикладных исследованиях используют стандартное нормальное распределение, стандартное распределение Вейбулла-Гнеденко, стандартное гамма-распределение и др. (см. ниже).
называют стандартным. В вероятностно-статистических методах принятия решений и других прикладных исследованиях используют стандартное нормальное распределение, стандартное распределение Вейбулла-Гнеденко, стандартное гамма-распределение и др. (см. ниже).
Применяют и другие преобразования случайных величин. Например, для положительной случайной величины  рассматривают
рассматривают 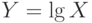 , где
, где 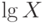 – десятичный логарифм числа
– десятичный логарифм числа  . Цепочка равенств
. Цепочка равенств

связывает функции распределения  и
и  .
.
При обработке данных используют такие характеристики случайной величины  как моменты порядка
как моменты порядка  , т.е. математические ожидания случайной величины
, т.е. математические ожидания случайной величины 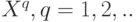 . Так, само математическое ожидание – это момент порядка 1. Для дискретной случайной величины момент порядка
. Так, само математическое ожидание – это момент порядка 1. Для дискретной случайной величины момент порядка  может быть рассчитан как
может быть рассчитан как
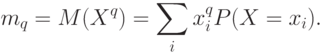
Для непрерывной случайной величины
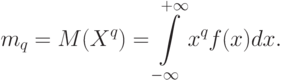
Моменты порядка  называют также начальными моментами порядка
называют также начальными моментами порядка  , в отличие от родственных характеристик – центральных моментов порядка
, в отличие от родственных характеристик – центральных моментов порядка  , задаваемых формулой
, задаваемых формулой
![\mu_q=M[(X-M(X))^q],\;q=2,3,...](/sites/default/files/tex_cache/7b7bfe61aca346f804d0c3147505d6a5.png)
Так, дисперсия – это центральный момент порядка 2.
Нормальное распределение и центральная предельная теорема. В вероятностно-статистических методах принятия решений часто идет речь о нормальном распределении. Иногда его пытаются использовать для моделирования распределения исходных данных (эти попытки не всегда являются обоснованными – см. ниже). Более существенно, что многие методы обработки данных основаны на том, что расчетные величины имеют распределения, близкие к нормальному.
Пусть 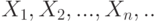 . – независимые одинаково распределенные случайные величины с математическими ожиданиями
. – независимые одинаково распределенные случайные величины с математическими ожиданиями 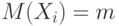 и дисперсиями
и дисперсиями 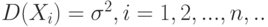 . Как следует из результатов 2.2,
. Как следует из результатов 2.2,

Рассмотрим приведенную случайную величину 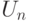 для суммы
для суммы  , а именно,
, а именно,
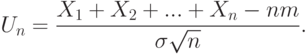
Как следует из формул (7), 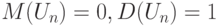 .
.
Центральная предельная теорема (для одинаково распределенных слагаемых). Пусть 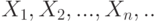 . – независимые одинаково распределенные случайные величины с математическими ожиданиями M(X_i)=m и дисперсиями
. – независимые одинаково распределенные случайные величины с математическими ожиданиями M(X_i)=m и дисперсиями 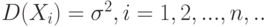 . Тогда для любого
. Тогда для любого  существует предел
существует предел
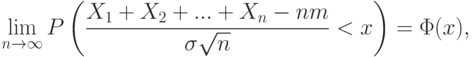
где 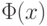 – функция стандартного нормального распределения.
– функция стандартного нормального распределения.
Подробнее о функции 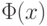 – см. ниже (читается "фи от икс", поскольку
– см. ниже (читается "фи от икс", поскольку  – греческая прописная буква "фи").
– греческая прописная буква "фи").
Центральная предельная теорема (ЦПТ) носит свое название по той причине, что она является центральным, наиболее часто применяющимся математическим результатом теории вероятностей и математической статистики. История ЦПТ занимает около 200 лет – с 1730 г., когда английский математик А.Муавр (1667–1754) опубликовал первый результат, относящийся к ЦПТ (о теореме Муавра-Лапласа см. ниже), по двадцатые – тридцатые годы ХХ в., когда финн Дж. У. Линдеберг, француз Поль Леви (1886–1971), югослав В. Феллер (1906–1970), русский А.Я. Хинчин (1894–1959) и другие ученые получили необходимые и достаточные условия справедливости классической центральной предельной теоремы.
Развитие рассматриваемой тематики на этом отнюдь не прекратилось – изучали случайные величины, не имеющие дисперсии, т.е. те, для которых
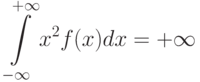
(академик Б.В.Гнеденко и др.), ситуацию, когда суммируются случайные величины (точнее, случайные элементы) более сложной природы, чем числа (академики Ю.В.Прохоров, А.А.Боровков и их соратники), и т.д.
Функция распределения 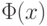 задается равенством
задается равенством
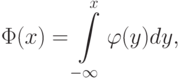
где 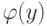 – плотность стандартного нормального распределения, имеющая довольно сложное выражение:
– плотность стандартного нормального распределения, имеющая довольно сложное выражение:
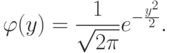
Здесь 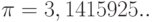 . – известное в геометрии число, равное отношению длины окружности к диаметру,
. – известное в геометрии число, равное отношению длины окружности к диаметру,  . – основание натуральных логарифмов (для запоминания этого числа обратите внимание, что 1828 – год рождения писателя Л.Н.Толстого). Как известно из математического анализа,
. – основание натуральных логарифмов (для запоминания этого числа обратите внимание, что 1828 – год рождения писателя Л.Н.Толстого). Как известно из математического анализа,
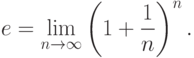
При обработке результатов наблюдений функцию нормального распределения не вычисляют по приведенным формулам, а находят с помощью специальных таблиц или компьютерных программ. Лучшие на русском языке "Таблицы математической статистики" составлены членами-корреспондентами АН СССР Л.Н. Большевым и Н.В.Смирновым [ [ 2.1 ] ].
Вид плотности стандартного нормального распределения 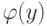 вытекает из математической теории, которую не имеем возможности здесь рассматривать, равно как и доказательство ЦПТ.
вытекает из математической теории, которую не имеем возможности здесь рассматривать, равно как и доказательство ЦПТ.
Для иллюстрации приводим небольшие таблицы функции распределения 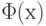 (табл.2.3) и ее квантилей (табл.2.4). Функция
(табл.2.3) и ее квантилей (табл.2.4). Функция 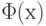 симметрична относительно 0, что отражается в табл.2.3–2.4.
симметрична относительно 0, что отражается в табл.2.3–2.4.
 |
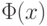 |
 |
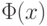 |
 |
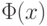 |
| -5,0 | 0,00000029 | -1,0 | 0,158655 | 2,0 | 0,9772499 |
| -4,0 | 0,00003167 | -0,5 | 0,308538 | 2,5 | 0,99379033 |
| -3,0 | 0,00134990 | 0,0 | 0,500000 | 3,0 | 0,99865010 |
| -2,5 | 0,00620967 | 0,5 | 0,691462 | 4,0 | 0,99996833 |
| -2,0 | 0,0227501 | 1,0 | 0,841345 | 5,0 | 0,99999971 |
| -1,5 | 0,0668072 | 1,5 | 0,9331928 |
Если случайная величина  имеет функцию распределения
имеет функцию распределения 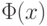 , то
, то  . Это утверждение доказывается в теории вероятностей, исходя из вида плотности вероятностей
. Это утверждение доказывается в теории вероятностей, исходя из вида плотности вероятностей 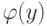 . Оно согласуется с аналогичным утверждением для характеристик приведенной случайной величины
. Оно согласуется с аналогичным утверждением для характеристик приведенной случайной величины 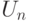 , что вполне естественно, поскольку ЦПТ утверждает, что при безграничном возрастании числа слагаемых функция распределения
, что вполне естественно, поскольку ЦПТ утверждает, что при безграничном возрастании числа слагаемых функция распределения 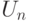 стремится к функции стандартного нормального распределения
стремится к функции стандартного нормального распределения 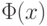 , причем при любом
, причем при любом  .
.