|
Здравствуйте! 4 июня я записалась на курс Прикладная статистика. Заплатила за получение сертификата. Изучала лекции, прошла Тест 1. Сегодня вижу, что я вне курса! Почему так произошло? |
Основы вероятностно-статистических методов описания неопределенностей
2.2. События и вероятности
Этот параграф содержит полные доказательства всех рассматриваемых утверждений.
События и вероятности. Исходное понятие при построении вероятностных моделей в задачах принятия решений - опыт (испытание). Примерами опытов являются проверка качества единицы продукции, бросание трех монет независимо друг от друга и т.д.
Первый шаг при построении вероятностной модели реального явления или процесса - выделение возможных исходов опыта. Их называют элементарными событиями. Обычно считают, что в первом примере возможны два исхода опыта - "единица продукции годная" и "единица продукции дефектная". Естественно принять, что при бросании монеты осуществляется одно из двух элементарных событий - "выпала решетка (цифра)" и "выпал герб". Таким образом, случаи "монета встала на ребро" или "монету не удалось найти" считаем невозможными.
При бросании трех монет элементарных событий значительно больше. Вот одно из них - "первая монета выпала гербом, вторая - решеткой, третья - снова гербом". Перечислим все элементарные события в этом опыте. Для этого обозначим выпадение герба буквой Г, а решетки - буквой Р. Имеется 23=8 элементарных событий: ГГГ, ГГР, ГРГ, ГРР, РГГ, РГР, РРГ, РРР - в каждой тройке символов первый показывает результат бросания первой монеты, второй - второй монеты, третий - третьей монеты.
Совокупность всех возможных исходов опыта, т.е. всех элементарных событий, называется пространством элементарных событий. Вначале мы ограничимся пространством элементарных событий, состоящим из конечного числа элементов.
С математической точки зрения пространство (совокупность) всех элементарных событий, возможных в опыте, - это некоторое множество, а элементарные события - его элементы. Однако в теории вероятностей для обозначения используемых понятий по традиции используются свои термины, отличающиеся от терминов теории множеств. В табл.2.1 установлено соответствие между терминологическими рядами этих двух математических дисциплин.
Как сложились два параллельных терминологических ряда? Основные понятия теории вероятностей и ее терминология сформировались в XVII-XVIII вв. Теория множеств возникла в конце XIX в. независимо от теории вероятностей и получила распространение в ХХ в.
Принятый в настоящее время аксиоматический подход к теории вероятностей, разработанный академиком АН СССР А.Н. Колмогоровым (1903-1987), дал возможность развивать эту дисциплину на базе теории множеств и теории меры. Этот подход позволил рассматривать теорию вероятностей и математическую статистику как часть математики, проводить рассуждения на математическом уровне строгости. В частности, было введено четкое различие между частотой и вероятностью, случайная величина стала рассматриваться как функция от элементарного исхода, и т.д. За основу методов статистического анализа данных стало возможным брать вероятностно-статистические модели, сформулированные в математических терминах. В результате удалось четко отделить строгие утверждения от обсуждения философских вопросов случайности, преодолеть подход на основе понятия равновозможности, имеющий ограниченное практическое значение. Наиболее существенно, что после работ А.Н. Колмогорова нет необходимости связывать вероятности тех или иных событий с пределами частот. Так называемые "субъективные вероятности" получили смысл экспертных оценок вероятностей.
После выхода (в 1933 г. на немецком языке и в 1936 г. - на русском) основополагающей монографии [ [ 2.7 ] ] аксиоматический подход к теории вероятностей стал общепринятым в научных исследованиях в этой области. Во многом перестроилось преподавание. Повысился научный уровень многих прикладных работ. Однако доколмогоровский традиционный подход оказался живучим. Распространены устаревшие и во многом неверные представления о теории вероятностей и математической статистике. Поэтому в настоящей лекции рассматриваем основные понятия, подходы, идеи, методы и результаты в этих областях, необходимые для их квалифицированного применения в задачах различных областей практической деятельности и научных исследований.
В послевоенные годы А.Н. Колмогоров формализовал понятие случайности на основе теории информации [ [ 2.9 ] ]. Грубо говоря, числовая последовательность является случайной, если ее нельзя заметно сжать без потери информации. Однако этот подход не был предназначен для использования в прикладных работах и преподавании. Он представляет собой важное методологическое и теоретическое продвижение.
Перейдем к основному понятию теории вероятностей - понятию вероятности события. В методологических терминах можно сказать, что вероятность события является мерой возможности осуществления события. В ряде случаев естественно считать, что вероятность события  - это число, к которому приближается отношение количества осуществлений события
- это число, к которому приближается отношение количества осуществлений события  к общему числу всех опытов (т.е. частота осуществления события
к общему числу всех опытов (т.е. частота осуществления события  ) - при увеличении числа опытов, проводящихся независимо друг от друга. Иногда можно предсказать это число из соображений равновозможности. Так, при бросании симметричной монеты и герб, и решетка имеют одинаковые шансы оказаться сверху, а именно, 1 шанс из 2, а потому вероятности выпадения герба и решетки равны 1/2.
) - при увеличении числа опытов, проводящихся независимо друг от друга. Иногда можно предсказать это число из соображений равновозможности. Так, при бросании симметричной монеты и герб, и решетка имеют одинаковые шансы оказаться сверху, а именно, 1 шанс из 2, а потому вероятности выпадения герба и решетки равны 1/2.
Однако этих соображений недостаточно для развития теории. Методологическое определение не дает численных значений. Не все вероятности можно оценивать как пределы частот, и неясно, сколько необходимо опытов. На основе идеи равновозможности можно решить ряд задач, но в большинстве практических ситуаций применить ее нельзя. Например, для оценки вероятности дефектности единицы продукции. Поэтому перейдем к определениям в рамках аксиоматического подхода на базе математической модели, предложенной А.Н. Колмогоровым (1933).
Определение 1. Пусть конечное множество 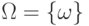 является пространством элементарных событий, соответствующим некоторому опыту. Пусть каждому
является пространством элементарных событий, соответствующим некоторому опыту. Пусть каждому 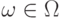 поставлено в соответствие неотрицательное число
поставлено в соответствие неотрицательное число  , называемое вероятностью элементарного события
, называемое вероятностью элементарного события 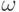 , причем сумма вероятностей всех элементарных событий равна 1, т.е.
, причем сумма вероятностей всех элементарных событий равна 1, т.е.
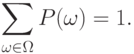 |
( 1) |
Тогда пара 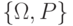 , состоящая из конечного множества
, состоящая из конечного множества  и неотрицательной функции
и неотрицательной функции  , определенной на
, определенной на  и удовлетворяющей условию (1), называется вероятностным пространством. Вероятность события
и удовлетворяющей условию (1), называется вероятностным пространством. Вероятность события  равна сумме вероятностей элементарных событий, входящих в
равна сумме вероятностей элементарных событий, входящих в  , т.е. определяется равенством
, т.е. определяется равенством
 |
( 2) |
Сконструирован математический объект, основной при построении вероятностных моделей. Рассмотрим примеры.
Пример 1. Бросанию монеты соответствует вероятностное пространство с  и
и  ; здесь обозначено:
; здесь обозначено: 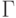 - выпал герб,
- выпал герб,  - выпала решетка.
- выпала решетка.
Пример 2. Проверке качества одной единицы продукции (в ситуации, описанной в романе А.Н. Толстого "Хождение по мукам" - см. выше) соответствует вероятностное пространство с  и
и 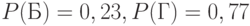 ; здесь обозначено: Б - дефектная единица продукции, Г - годная единица продукции; значение вероятности 0,23 взято из слов Струкова.
; здесь обозначено: Б - дефектная единица продукции, Г - годная единица продукции; значение вероятности 0,23 взято из слов Струкова.
Отметим, что приведенное выше определение вероятности 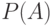 согласуется с интуитивным представлением о связи вероятностей события и входящих в него элементарных событий, а также с распространенным мнением, согласно которому "вероятность события
согласуется с интуитивным представлением о связи вероятностей события и входящих в него элементарных событий, а также с распространенным мнением, согласно которому "вероятность события  - число от 0 до 1, которое представляет собой предел частоты реализации события
- число от 0 до 1, которое представляет собой предел частоты реализации события  при неограниченном числе повторений одного и того же комплекса условий".
при неограниченном числе повторений одного и того же комплекса условий".
Из определения вероятности события, свойств символа суммирования и равенства (1) вытекает, что
 |
( 3) |
Для несовместных событий  и
и  согласно формуле (3)
согласно формуле (3) 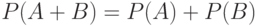 . Последнее утверждение называют также теоремой сложения вероятностей.
. Последнее утверждение называют также теоремой сложения вероятностей.
При практическом применении вероятностно-статистических методов принятия решений постоянно используется понятие независимости. Например, при применении статистических методов управления качеством продукции говорят о независимых измерениях значений контролируемых параметров у включенных в выборку единиц продукции, о независимости появления дефектов одного вида от появления дефектов другого вида и т.д. Независимость случайных событий понимается в вероятностных моделях в следующем смысле.
Определение 2. События  и
и  называются независимыми, если
называются независимыми, если 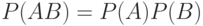 . Несколько событий
. Несколько событий  . называются независимыми, если
. называются независимыми, если 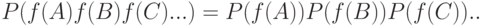 . для любого набора
. для любого набора 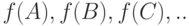 ., где
., где 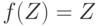 либо
либо 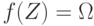 . Если события
. Если события  . независимы, то
. независимы, то 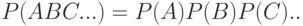 .
.
Это определение соответствует интуитивному представлению о независимости: осуществление или неосуществление одного события не должно влиять на осуществление или неосуществление другого. Иногда соотношение 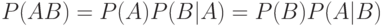 , справедливое при
, справедливое при  , называют также теоремой умножения вероятностей.
, называют также теоремой умножения вероятностей.
Утверждение 1. Пусть события  и
и  независимы. Тогда события
независимы. Тогда события 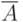 и
и  независимы, события
независимы, события 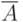 и
и  независимы, события
независимы, события  и
и  независимы (здесь
независимы (здесь 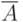 - событие, противоположное
- событие, противоположное  , и
, и  - событие, противоположное
- событие, противоположное  ).
).
Действительно, из свойства в ) в (3) следует, что для событий  и
и 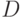 , произведение которых пусто,
, произведение которых пусто, 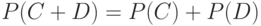 . Поскольку пересечение
. Поскольку пересечение 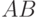 и
и  пусто, а объединение есть
пусто, а объединение есть  , то
, то 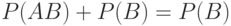 . Так как
. Так как  и
и  независимы, то
независимы, то 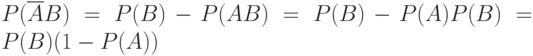 . Заметим теперь, что из соотношений (1) и (2) следует, что
. Заметим теперь, что из соотношений (1) и (2) следует, что 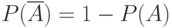 . Значит,
. Значит, 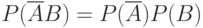 .
.
Bывод равенства 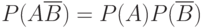 отличается от предыдущего лишь заменой всюду
отличается от предыдущего лишь заменой всюду  на
на  , а
, а  на
на  .
.
Для доказательства независимости 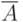 и
и  воспользуемся тем, что события
воспользуемся тем, что события 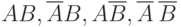 не имеют попарно общих элементов, а в сумме составляют все пространство элементарных событий. Следовательно,
не имеют попарно общих элементов, а в сумме составляют все пространство элементарных событий. Следовательно, 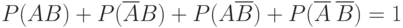 . Bоспользовавшись ранее доказанными соотношениями, получаем, что
. Bоспользовавшись ранее доказанными соотношениями, получаем, что
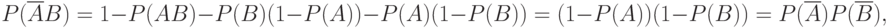
Пример 3. Рассмотрим опыт, состоящий в бросании игрального кубика, на гранях которого написаны числа 1, 2, 3, 4, 5, 6. Считаем, что все грани имеют одинаковые шансы оказаться наверху. Построим соответствующее вероятностное пространство. Покажем, что события "наверху - грань с четным номером" и "наверху - грань с числом, делящимся на 3" являются независимыми.
Разбор примера. Пространство элементарных исходов состоит из 6 элементов: "наверху - грань с 1", "наверху - грань с 2",..., "наверху - грань с 6". Событие "наверху - грань с четным номером" состоит из трех элементарных событий - когда наверху оказывается 2, 4 или 6. Событие "наверху - грань с числом, делящимся на 3" состоит из двух элементарных событий - когда наверху оказывается 3 или 6. Поскольку все грани имеют одинаковые шансы оказаться наверху, то все элементарные события должны иметь одинаковую вероятность. Поскольку всего имеется 6 элементарных событий, то каждое из них имеет вероятность 1/6. По определению 1 событие "наверху - грань с четным номером" имеет вероятность 1/2, а событие "наверху - грань с числом, делящимся на 3" - вероятность 1/3. Произведение этих событий состоит из одного элементарного события "наверху - грань с 6", а потому имеет вероятность 1/6. Поскольку 1/6 = 1/2 х 1/3, то рассматриваемые события являются независимыми в соответствии с определением независимости.
В вероятностных моделях процедур принятия решений с помощью понятия независимости событий можно придать точный смысл понятию "независимые испытания". Для этого рассмотрим сложный опыт, состоящий в проведении двух испытаний. Эти испытания называются независимыми, если любые два события  и
и  , из которых
, из которых  определяется по исходу первого испытания, а
определяется по исходу первого испытания, а  - по исходу второго, являются независимыми.
- по исходу второго, являются независимыми.
Пример 4. Опишем вероятностное пространство, соответствующее бросанию двух монет независимо друг от друга.
Разбор примера. Пространство элементарных событий состоит из четырех элементов: ГГ, ГР, РГ, РР (запись ГГ означает, что первая монета выпала гербом и вторая - тоже гербом; запись РГ - первая - решеткой, а вторая - гербом, и т.д.). Поскольку события "первая монета выпала решеткой" и "вторая монета выпала гербом" являются независимыми по определению независимых испытаний и вероятность каждого из них равна 1/2, то вероятность РГ равна 1/4. Аналогично вероятность каждого из остальных элементарных событий также равна 1/4.
Пример 5. Опишем вероятностное пространство, соответствующее проверке качества двух единиц продукции независимо друг от друга, если вероятность дефектности равна  .
.
Разбор примера. Пространство элементарных событий состоит из четырех элементов:
-
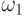 - обе единицы продукции годны;
- обе единицы продукции годны; -
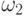 - первая единица продукции годна, а вторая - дефектна;
- первая единица продукции годна, а вторая - дефектна; -
 - первая единица продукции дефектна, а вторая - годна;
- первая единица продукции дефектна, а вторая - годна; -
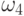 - обе единицы продукции являются дефектными.
- обе единицы продукции являются дефектными.
Вероятность того, что единица продукции дефектна, есть  , а потому вероятность того, что имеет место противоположное событие, т.е. единица продукции годна, есть
, а потому вероятность того, что имеет место противоположное событие, т.е. единица продукции годна, есть 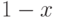 . Поскольку результат проверки первой единицы продукции не зависит от такового для второй, то
. Поскольку результат проверки первой единицы продукции не зависит от такового для второй, то 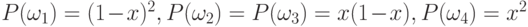 .
.
Замечание об условных вероятностях. В некоторых задачах прикладной статистики оказывается полезным такое понятие, как условная вероятность 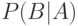 - вероятность осуществления события
- вероятность осуществления события  при условии, что событие
при условии, что событие  произошло. При
произошло. При  по определению
по определению
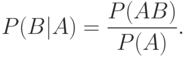
Для независимых событий  и
и  , очевидно,
, очевидно, 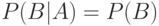 . Это равенство эквивалентно определению независимости. Понятия условной вероятности и независимости введены А. Муавром в 1718 г.
. Это равенство эквивалентно определению независимости. Понятия условной вероятности и независимости введены А. Муавром в 1718 г.
Необходимо иметь в виду, что для справедливости равенства 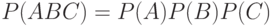 недостаточно попарной независимости событий
недостаточно попарной независимости событий  ,
,  и
и  . Рассмотрим классический пример [
[
2.3
]
, с.46]. Пусть одна грань тетраэдра окрашена в красный цвет, вторая - в зеленый. Третья грань окрашена в синий цвет и четвертая - во все эти три цвета. Пусть событие
. Рассмотрим классический пример [
[
2.3
]
, с.46]. Пусть одна грань тетраэдра окрашена в красный цвет, вторая - в зеленый. Третья грань окрашена в синий цвет и четвертая - во все эти три цвета. Пусть событие  состоит в том, что грань, на которую упал тетраэдр при бросании, окрашена красным (полностью или частично), событие
состоит в том, что грань, на которую упал тетраэдр при бросании, окрашена красным (полностью или частично), событие  - зеленым, событие
- зеленым, событие  - синим. Пусть при бросании все четыре грани тетраэдра имеют одинаковые шансы оказаться внизу. Поскольку граней четыре и две из них имеют в окраске красный цвет, то
- синим. Пусть при бросании все четыре грани тетраэдра имеют одинаковые шансы оказаться внизу. Поскольку граней четыре и две из них имеют в окраске красный цвет, то 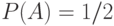 . Легко подсчитать, что
. Легко подсчитать, что
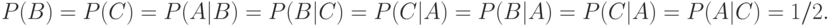
События  ,
,  и
и  , таким образом, попарно независимы. Однако если известно, что осуществились одновременно события
, таким образом, попарно независимы. Однако если известно, что осуществились одновременно события  и
и  , то это значит, что тетраэдр встал на грань, содержащую все три цвета, т.е. осуществилось и событие
, то это значит, что тетраэдр встал на грань, содержащую все три цвета, т.е. осуществилось и событие  . Следовательно,
. Следовательно, 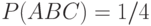 , в то время как для независимых событий должно быть
, в то время как для независимых событий должно быть 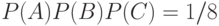 . Следовательно, события
. Следовательно, события  ,
,  и
и  в совокупности зависимы, хотя попарно независимы.
в совокупности зависимы, хотя попарно независимы.
Предположим, что событие  может осуществиться с одним и только с одним из
может осуществиться с одним и только с одним из  попарно несовместных событий
попарно несовместных событий 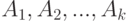 . Тогда
. Тогда
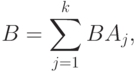
где события 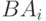 и
и  с разными индексами
с разными индексами  и
и 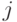 несовместны. По теореме сложения вероятностей
несовместны. По теореме сложения вероятностей
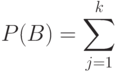
Воспользовавшись теоремой умножения, находим, что
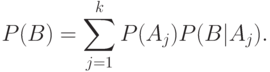
Получена так называемая "формула полной вероятности". Она широко использовалась математиками при конкретных расчетах еще в начале XVIII века, но впервые была сформулирована как одно из основных утверждений теории вероятностей П.Лапласом лишь в конце этого века. Ниже она применяется, в частности, при нахождении среднего выходного уровня дефектности в задачах статистического обеспечения качества продукции.
Применим формулу полных вероятностей для вывода так называемых "формул Байеса", которые иногда используют при проверке статистических гипотез. Требуется найти вероятность события  , если известно, что событие
, если известно, что событие  произошло. Согласно теореме умножения
произошло. Согласно теореме умножения
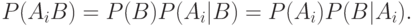
Следовательно,
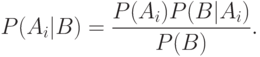
Используя формулу полной вероятности для знаменателя, находим, что
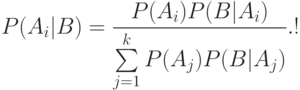
Две последние формулы и называют обычно формулами Байеса. Общая схема их использования такова. Пусть событие  может протекать в различных условиях, относительно которых может быть сделано
может протекать в различных условиях, относительно которых может быть сделано  гипотез
гипотез 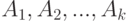 . Априорные (от a priori (лат.) - до опыта) вероятности этих гипотез есть
. Априорные (от a priori (лат.) - до опыта) вероятности этих гипотез есть 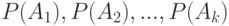 . Известно также, что при справедливости гипотезы
. Известно также, что при справедливости гипотезы  вероятность осуществления события
вероятность осуществления события  равна
равна 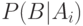 . Произведен опыт, в результате которого событие
. Произведен опыт, в результате которого событие  наступило.
Естественно после этого уточнить оценки вероятностей гипотез. Апостериорные (от a posteriori (лат.) - на основе опыта) оценки вероятностей гипотез
наступило.
Естественно после этого уточнить оценки вероятностей гипотез. Апостериорные (от a posteriori (лат.) - на основе опыта) оценки вероятностей гипотез 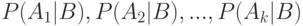 даются формулами Байеса. В прикладной статистике существует направление "байесовская статистика", в которой, в частности, на основе априорного распределения параметров после проведения измерений, наблюдений, испытаний, опытов, анализов вычисляют уточненные оценки параметров.
даются формулами Байеса. В прикладной статистике существует направление "байесовская статистика", в которой, в частности, на основе априорного распределения параметров после проведения измерений, наблюдений, испытаний, опытов, анализов вычисляют уточненные оценки параметров.
Случайные величины и их математические ожидания. Случайная величина - это величина, значение которой зависит от случая, т.е. от элементарного события 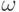 . Таким образом, случайная величина - это функция, определенная на пространстве элементарных событий
. Таким образом, случайная величина - это функция, определенная на пространстве элементарных событий  . Примеры случайных величин: количество гербов, выпавших при независимом бросании двух монет; число, выпавшее на верхней грани игрального кубика; число дефектных единиц продукции среди проверенных.
. Примеры случайных величин: количество гербов, выпавших при независимом бросании двух монет; число, выпавшее на верхней грани игрального кубика; число дефектных единиц продукции среди проверенных.
Определение случайной величины  как функции от элементарного события
как функции от элементарного события 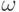 , т.е. функции
, т.е. функции 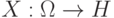 , отображающей пространство элементарных событий
, отображающей пространство элементарных событий  в некоторое множество
в некоторое множество  , казалось бы, содержит в себе противоречие. О чем идет речь - о величине или о функции? Дело в том, что наблюдается всегда лишь так называемая "реализация случайной величины", т.е. ее значение, соответствующее именно тому элементарному исходу опыта (элементарному событию), которое осуществилось в конкретной реальной ситуации. То есть наблюдается именно "величина". А функция от элементарного события - это теоретическое понятие, основа вероятностной модели реального явления или процесса.
, казалось бы, содержит в себе противоречие. О чем идет речь - о величине или о функции? Дело в том, что наблюдается всегда лишь так называемая "реализация случайной величины", т.е. ее значение, соответствующее именно тому элементарному исходу опыта (элементарному событию), которое осуществилось в конкретной реальной ситуации. То есть наблюдается именно "величина". А функция от элементарного события - это теоретическое понятие, основа вероятностной модели реального явления или процесса.
Отметим, что элементы  - это не обязательно числа. Ими могут быть и последовательности чисел (вектора), и функции, и математические объекты иной природы, в частности, нечисловой (упорядочения и другие бинарные отношения, множества, нечеткие множества и др.) [
[
2.16
]
]. Однако наиболее часто рассматриваются вероятностные модели, в которых элементы
- это не обязательно числа. Ими могут быть и последовательности чисел (вектора), и функции, и математические объекты иной природы, в частности, нечисловой (упорядочения и другие бинарные отношения, множества, нечеткие множества и др.) [
[
2.16
]
]. Однако наиболее часто рассматриваются вероятностные модели, в которых элементы  - числа, т.е.
- числа, т.е.  . В иных случаях обычно используют термины "случайный вектор", "случайное множество", "случайное упорядочение", "случайный элемент" и др.
. В иных случаях обычно используют термины "случайный вектор", "случайное множество", "случайное упорядочение", "случайный элемент" и др.
Рассмотрим случайную величину с числовыми значениями. Часто оказывается полезным связать с этой функцией число - ее "среднее значение" или, как говорят, "среднюю величину", "показатель центральной тенденции". По ряду причин, некоторые из которых будут ясны из дальнейшего, в качестве "среднего значения" обычно используют математическое ожидание.
Определение 3. Математическим ожиданием случайной величины  называется число
называется число
 |
( 4) |
т.е. математическое ожидание случайной величины - это взвешенная сумма значений случайной величины с весами, равными вероятностям соответствующих элементарных событий.
 . Вычислим математическое ожидание числа, выпавшего на верхней грани игрального кубика. Непосредственно из определения 3 следует, что
. Вычислим математическое ожидание числа, выпавшего на верхней грани игрального кубика. Непосредственно из определения 3 следует, что

Утверждение 2. Пусть случайная величина  принимает значения
принимает значения 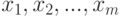 . Тогда справедливо равенство
. Тогда справедливо равенство
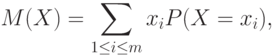 |
( 5) |
т.е. математическое ожидание случайной величины - это взвешенная сумма значений случайной величины с весами, равными вероятностям того, что случайная величина принимает определенные значения.
В отличие от (4), где суммирование проводится непосредственно по элементарным событиям, случайное событие 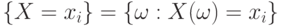 может состоять из нескольких элементарных событий.
может состоять из нескольких элементарных событий.
Иногда соотношение (5) принимают как определение математического ожидания. Однако с помощью определения 3, как показано далее, более легко установить свойства математического ожидания, нужные для построения вероятностных моделей реальных явлений, чем с помощью соотношения (5).
Для доказательства соотношения (5) сгруппируем в (4) члены с одинаковыми значениями случайной величины  :
:
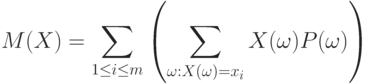
Поскольку постоянный множитель можно вынести за знак суммы, то
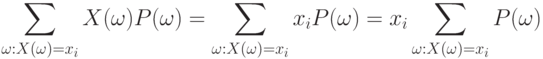
По определению вероятности события
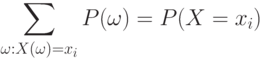
С помощью двух последних соотношений получаем требуемое:
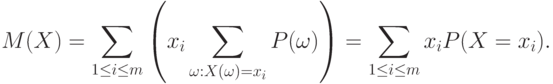
Понятие математического ожидания в вероятностно-статистической теории соответствует понятию центра тяжести в механике. Поместим в точки 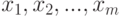 на числовой оси массы
на числовой оси массы 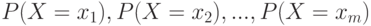 соответственно. Тогда равенство (5) означает, что центр тяжести этой системы материальных точек совпадает с математическим ожиданием, что показывает естественность определения 3.
соответственно. Тогда равенство (5) означает, что центр тяжести этой системы материальных точек совпадает с математическим ожиданием, что показывает естественность определения 3.
Утверждение 3. Пусть  - случайная величина,
- случайная величина, 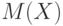 - ее математическое ожидание,
- ее математическое ожидание,  - некоторое число. Тогда
- некоторое число. Тогда
![1)\; M(a)=a;\;2)\;M(X-M(X))=0;\;3)\;M[(X-a)^2]=M[(X-M(X))^2]+(a-M(X))^2.](/sites/default/files/tex_cache/44a38fcb91c8bbd3892bad08ea9f137e.png)
Для доказательства рассмотрим сначала случайную величину, являющуюся постоянной, 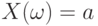 т.е. функция
т.е. функция  отображает пространство элементарных событий
отображает пространство элементарных событий  в единственную точку
в единственную точку  . Поскольку постоянный множитель можно выносить за знак суммы, то
. Поскольку постоянный множитель можно выносить за знак суммы, то
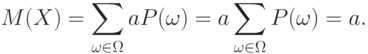
Если каждый член суммы разбивается на два слагаемых, то и вся сумма разбивается на две суммы, из которых первая составлена из первых слагаемых, а вторая - из вторых. Следовательно, математическое ожидание суммы двух случайных величин  , определенных на одном и том же пространстве элементарных событий, равно сумме математических ожиданий
, определенных на одном и том же пространстве элементарных событий, равно сумме математических ожиданий 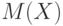 и
и 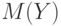 этих случайных величин:
этих случайных величин:
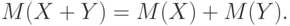
А потому 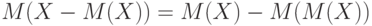 . Как показано выше,
. Как показано выше, 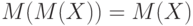 . Следовательно,
. Следовательно, 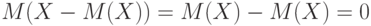 .
.
Поскольку 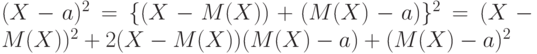 , то
, то ![M[(X - a)^2] =M(X - M(X))^2 + M\{2(X - M(X))(M(X) - a)\} +M[(M(X) - a)^2]](/sites/default/files/tex_cache/6084b0f8860654ca73d6330192cb9940.png) . Упростим последнее равенство. Как показано в начале доказательства утверждения 3, математическое ожидание константы - сама эта константа, а потому
. Упростим последнее равенство. Как показано в начале доказательства утверждения 3, математическое ожидание константы - сама эта константа, а потому ![M[(M(X) - a)^2] = (M(X) - a)^2](/sites/default/files/tex_cache/b3da120a29979226f32bb5ef9f8e2360.png) . Поскольку постоянный множитель можно выносить за знак суммы, то
. Поскольку постоянный множитель можно выносить за знак суммы, то 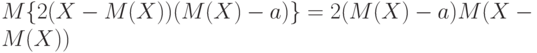 . Правая часть последнего равенства равна 0, поскольку, как показано выше,
. Правая часть последнего равенства равна 0, поскольку, как показано выше, 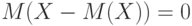 . Следовательно,
. Следовательно, ![M[(X - a)^2]=M[(X - M(X))^2]+ (a - M(X))^2](/sites/default/files/tex_cache/9ad0ecf5d6c02245643d742ea0a82f15.png) , что и требовалось доказать.
, что и требовалось доказать.
Из сказанного вытекает, что ![M[(X - a)^2]](/sites/default/files/tex_cache/57528be79d455632ae36e98c4a40e3c1.png) достигает минимума по
достигает минимума по  , равного
, равного ![M[(X - M(X))^2]](/sites/default/files/tex_cache/045dede902afc484d1cb80a5da3d86c1.png) , при
, при 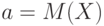 , поскольку второе слагаемое в равенстве (3) всегда неотрицательно и равно нулю только при указанном значении
, поскольку второе слагаемое в равенстве (3) всегда неотрицательно и равно нулю только при указанном значении  .
.
Утверждение 4. Пусть случайная величина  принимает значения
принимает значения 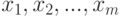 , а
, а  - некоторая функция числового аргумента. Тогда
- некоторая функция числового аргумента. Тогда
![M[f(X)]=\sum_{1\le i\le m} f(x_i)P(X=x_i).](/sites/default/files/tex_cache/a366611ca86a8ec729b1df96f1ae46b3.png)
Для доказательства сгруппируем в правой части равенства (4), определяющего математическое ожидание, члены с одинаковыми значениями  :
:
![M[f(X)]=\sum_{1\le i\le m}
\left(
\sum_{\omega:X(\omega)=x_i} f(X(\omega))P(\omega)
\right).](/sites/default/files/tex_cache/e21a8b554e2d5263788eea1df96e8a17.png)
Пользуясь тем, что постоянный множитель можно выносить за знак суммы, и определением вероятности случайного события (2), получаем
![M[f(X)]=\sum_{1\le i\le m}
\left(
f(x_i)\sum_{\omega:X(\omega)=x_i}P(\omega)
\right)
=\sum_{1\le i\le m} f(x_i)P(X=x_i),](/sites/default/files/tex_cache/0f1ba5d4bba42f0b3f563777bc8b71bb.png)
что и требовалось доказать.
Утверждение 5. Пусть  и
и  - случайные величины, определенные на одном и том же пространстве элементарных событий,
- случайные величины, определенные на одном и том же пространстве элементарных событий,  и
и  - некоторые числа. Тогда
- некоторые числа. Тогда 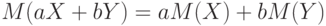 .
.
С помощью определения математического ожидания и свойств символа суммирования получаем цепочку равенств:
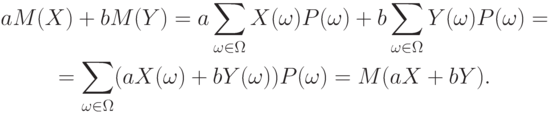
Требуемое доказано.
Выше показано, как зависит математическое ожидание от перехода к другому началу отсчета и к другой единице измерения (переход 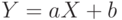 ), а также к функциям от случайных величин. Полученные результаты постоянно используются в технико-экономическом анализе, при оценке финансово-хозяйственной деятельности предприятия, при переходе от одной валюты к другой во внешнеэкономических расчетах, в нормативно-технической документации и др. Рассматриваемые результаты позволяют применять одни и те же расчетные формулы при различных параметрах масштаба и сдвига.
), а также к функциям от случайных величин. Полученные результаты постоянно используются в технико-экономическом анализе, при оценке финансово-хозяйственной деятельности предприятия, при переходе от одной валюты к другой во внешнеэкономических расчетах, в нормативно-технической документации и др. Рассматриваемые результаты позволяют применять одни и те же расчетные формулы при различных параметрах масштаба и сдвига.
Независимость случайных величин - одно из базовых понятий теории вероятностей, лежащее в основе практически всех вероятностно-статистических методов принятия решений.
Определение 4. Случайные величины  и
и  , определенные на одном и том же пространстве элементарных событий, называются независимыми, если для любых чисел
, определенные на одном и том же пространстве элементарных событий, называются независимыми, если для любых чисел  и
и  независимы события
независимы события 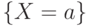 и
и  .
.
Утверждение 6. Если случайные величины  и
и  независимы,
независимы,  и
и  - некоторые числа, то случайные величины
- некоторые числа, то случайные величины 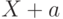 и
и  также независимы.
также независимы.
Действительно, события 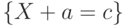 и
и 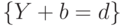 совпадают с событиями
совпадают с событиями 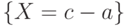 и
и  соответственно, а потому независимы.
соответственно, а потому независимы.
Пример 7. Случайные величины, определенные по результатам различных испытаний в схеме независимых испытаний, сами независимы. Это вытекает из того, что события, с помощью которых определяется независимость случайных величин, определяются по результатам различных испытаний, а потому независимы по определению независимых испытаний.
В вероятностно-статистических методах принятия решений постоянно используется следующий факт: если  и
и  - независимые случайные величины,
- независимые случайные величины,  и
и 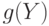 - случайные величины, полученные из
- случайные величины, полученные из  и
и  с помощью некоторых функций
с помощью некоторых функций  и
и 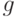 , то
, то  и
и 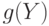 - также независимые случайные величины. Например, если
- также независимые случайные величины. Например, если  и
и  независимы, то
независимы, то 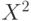 и
и  независимы,
независимы, 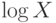 и
и 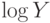 независимы. Доказательство рассматриваемого факта - тема одной из контрольных задач в конце лекции.
независимы. Доказательство рассматриваемого факта - тема одной из контрольных задач в конце лекции.
Подавляющее большинство вероятностно-статистических моделей, используемых на практике, основывается на понятии независимых случайных величин. Так, результаты наблюдений, измерений, испытаний, анализов, опытов обычно моделируются независимыми случайными величинами. Часто считают, что наблюдения проводятся согласно схеме независимых испытаний. Например, результаты финансово-хозяйственной деятельности предприятий, выработка рабочих, результаты (данные) измерений контролируемого параметра у изделий, отобранных в выборку при статистическом регулировании технологического процесса, ответы потребителей при маркетинговом опросе и другие типы данных, используемых при принятии решений, обычно рассматриваются как независимые случайные величины, векторы или элементы. Причина такой популярности понятия независимости случайных величин состоит в том, что к настоящему времени теория продвинута существенно дальше для независимых случайных величин, чем для зависимых.
Часто используется следующее свойство независимых случайных величин.
Утверждение 7. Если случайные величины  и
и  независимы, то математическое ожидание произведения
независимы, то математическое ожидание произведения 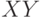 равно произведению математических ожиданий
равно произведению математических ожиданий  и
и  , т.е.
, т.е.  .
.
Доказательство. Пусть  принимает значения
принимает значения 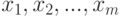 , в то время как
, в то время как  принимает значения
принимает значения 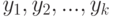 . Сгруппируем в задающей
. Сгруппируем в задающей 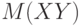 сумме члены, в которых
сумме члены, в которых  и
и  принимают фиксированные значения:
принимают фиксированные значения:
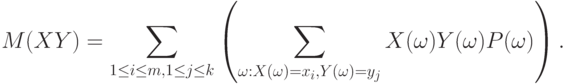 |
( 6) |
Поскольку постоянный множитель можно вынести за знак суммы, то
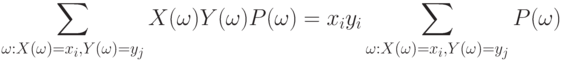
Из последнего равенства и определения вероятности события заключаем, что равенство (6) можно преобразовать к виду

Так как  и
и  независимы, то
независимы, то  . Воспользовавшись этим равенством и свойством символа суммирования
. Воспользовавшись этим равенством и свойством символа суммирования

заключаем, что
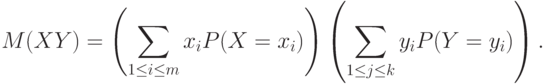 |
( 7) |
Из равенства (5) следует, что первый сомножитель в правой части (7) есть 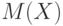 , а второй -
, а второй - 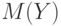 , что и требовалось доказать.
, что и требовалось доказать.
Пример 8. Построим пример, показывающий, что из равенства  не следует независимость случайных величин
не следует независимость случайных величин  и
и  . Пусть вероятностное пространство состоит из трех равновероятных элементов
. Пусть вероятностное пространство состоит из трех равновероятных элементов  . Пусть
. Пусть
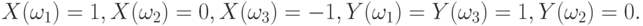
Тогда 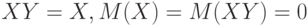 , следовательно,
, следовательно, 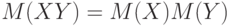 . Однако при этом
. Однако при этом 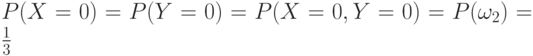 , в то время как вероятность события
, в то время как вероятность события 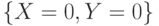 в случае независимых
в случае независимых  и
и  должна была равняться
должна была равняться 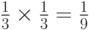 .
.
Независимость нескольких случайных величин 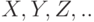 . означает по определению, что для любых чисел
. означает по определению, что для любых чисел 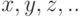 . справедливо равенство
. справедливо равенство
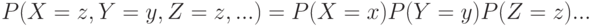
Например, если случайные величины определяются по результатам различных испытаний в схеме независимых испытаний, то они независимы.


 событий
событий 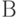
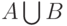
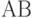 событий
событий 