Объектно-ориентированный подход к теории игр
Теорема 21.1. В матричной игре с матрицей выигрышей 
имеет место
В этой теореме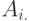 
обозначает 
-ую строку, а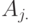 
- 
-ый столбец.
Несмотря на наличие этой теоремы вопрос конкретного определения оптимальных стратегий является очень сложным.
Мы в нашем курсе проведем моделирование матричной игры и проверим ряд известных решений некоторых игр. Начнем с программирования класса матричной игры.
![\begin{verbatim}
class TGame
{
protected double[,] A;
protected int m = 0, n = 0;
Random rnd;
public TGame()
{
rnd = new Random();
}
public double Calc(double[] X, double[] Y, int Count)
{
double res = 0;
int i, j;
for (int k = 0; k < Count; k++)
{
i = Release(X, m);
j = Release(Y, n);
res += GetAij(i, j);
}
return res / (double)Count;
}
\end{verbatim}](/sites/default/files/tex_cache/1fea0a0a5e9062b585017a0f3b28c219.png)
![\begin{verbatim}
public int Release(double[] Z, int N)
{
double p = rnd.NextDouble();
double a = 0;
for (int i = 1; i <= N; i++)
{
a += Z[i];
if (p <= a)
{
return i;
}
}
return N;
}
public double GetAij(int i, int j)
{
return A[i, j];
}
public double GetC(double[] X, double[] Y)
{
double res = 0;
int i, j;
for (i = 1; i <= m; i++)
{
for (j = 1; j <= n; j++)
{
res += A[i, j] * X[i] * Y[j];
}
}
return res;
}
}
\end{verbatim}](/sites/default/files/tex_cache/d4cfc1359fb6c7095d359850fbd8594a.png)
Теперь создадим два наследных класса, в которых мы реализуем две матричные игры.
![\begin{verbatim}
class TGame1 : TGame
{
public TGame1()
: base()
{
m = 2;
n = 2;
A = new double[3, 3];
A[1, 1] = 0;
A[1, 2] = 1;
A[2, 1] = 1;
A[2, 2] = 0;
}
}
class TGame2 : TGame
{
public TGame2()
: base()
{
m = 3;
n = 3;
A = new double[4, 4];
A[1, 1] = 0;
A[1, 2] = 1;
A[1, 3] = -2;
A[2, 1] = -1;
A[2, 2] = 0;
A[2, 3] = 3;
A[3, 1] = 2;
A[3, 2] = -3;
A[3, 3] = 0;
}
}
\end{verbatim}](/sites/default/files/tex_cache/595123a13f71660cb9edfdfd5bbc1270.png)
Класс 
- это самая простая нетривиальная игра. По сути
это игра в "чет--нечет". В этой игре нет равновесных чистых
стратегий, а в смешанных стратегиях эта игра имеет следующее
решение
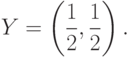
, представляет собой
более сложную игру со следующей платежной матрицей
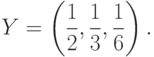
Проверим эти решения с помощью наших классов.
![\begin{verbatim}
double[] X;
double[] Y;
TGame1 Game1 = new TGame1();
X = new double[3] {0, 0.5, 0.5 };
Y = new double[3] {0, 0.5, 0.5 };
Console.WriteLine("Game1: theory = {0}, Res = {1}",
Game1.GetC(X, Y), Game1.Calc(X, Y, 1000000));
TGame2 Game2 = new TGame2();
X = new double[4] { 0, 0.5, 1.0 / 3.0, 1.0 / 6.0 };
Y = new double[4] { 0, 0.5, 1.0 / 3.0, 1.0 / 6.0 };
Console.WriteLine("Game2: theory = {0}, Res = {1}",
Game2.GetC(X, Y), Game2.Calc(X, Y, 1000000));
\end{verbatim}](/sites/default/files/tex_cache/8e01474ebebe68fec9547d5f74160ebf.png)
После запуска мы получим примерно следующее:
Ключевые термины
Антагонистичная игра - игра двух игроков с нулевой суммой.
Ситуация в игре - набор выбранных стратегий всех игроков.
Ситуация равновесия - такая ситуация, при которой ни один из игроков не заинтересован в изменении стратегии.
Смешанная стратегия - случайная величина, значениями которой являются стратегии игрока.
Теория игр - прикладная математическая дисциплина, в которой изучаются методы нахождения оптимальных решений в условиях неопределенности и ситуациях противодействия со стороны других игроков.
Краткие итоги: Рассмотрены постановки игр. Для матричных игр приведено объектно-ориентированное моделирование игр. С помощью статистического моделирования исследованы некоторые матричные игры.