Современные численные методы в объектно-ориентированном изложении на C#
[+]
Опубликован: 18.05.2011 | Доступ: свободный | Студентов: 976 / 106 | Оценка: 4.40 / 4.20 | Длительность: 12:30:00
Тема: Программирование
Специальности: Программист, Архитектор программного обеспечения
Теги: objective-c, алгоритмы, анализ, вычисления, графика, динамическая система, дифференциальные уравнения, игры, коэффициенты Фурье, кубический сплайн, матричная игра, машина поста, метод Эйлера, методы рунге-кутты, метрическое пространство, моделирование, программирование, процедуры, теория, трансцендентное уравнение, функциональное пространство, элементы
Лекция 7:

Научное программирование
A
|
версия для печати
< Лекция 6 || Лекция 7: 123 || Лекция 8 >

Лабораторная работа "Вычислительные процедуры"

Цель занятия

Продемонстрировать на практике различные вычислительные процедуры. Научится самостоятельно реализовывать вычислительные процедуры для решения задач численного анализа.

Сценарий лабораторной работы

  1. Рассмотреть следующую задачу Коши для системы обыкновенных дифференциальных уравнений
    x_1'(t)=a_{11}x_1(t)+a_{12}x_2(t)
    x_2'(t)=a_{21}x_1(t)+a_{22}x_2(t)
    x_1(0)=x_{10}
    x_2(0)=x_{20}
  2. Написать программу на языке C#, реализующую метод Рунге-Кутта для приближенного решения этой задачи на отрезке [0,T].
  3. Провести вычислительные эксперименты с различными значениями коэффициентов a_{ij}, i,j=1,2.
  4. Выделить эксперименты в которых наблюдается устойчивость решений по начальным данным x_{i0}, i=1,2.
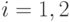  5. Построить соответствующие графики

Указания

Для исследования устойчивости решений необходимо рассмотреть собственные значения матрицы

A=\left(% \begin{array}{cc} a_{11} & a_{12} \\ a_{21} & a_{22} \\ \end{array}% \right).
Если собственные значения этой матрицы имеют отрицательные вещественные части, то решения задачи Коши будут устойчивыми.

Дальше >>
< Лекция 6 || Лекция 7: 123 || Лекция 8 >

Вопросы и ответы

вопросов: 0