|
Добрый день можно поинтересоваться где брать литературу предложенную в курсе ?Большинство книг я не могу найти в известных источниках |
Влияние стратегий наблюдения выходных сигналов на построение тестов для схем с памятью
24.2 Символьное моделирование
Приведенное выше определение 24.2 обнаруживаемости неисправностей для последовательностных схем дано фактически на функциональном уровне и требует явного моделирования для каждого начального состояния исправной и неисправной схем. Рассмотрим кратную стратегию наблюдения выходных сигналов и символьное моделирование неисправных последовательных схем. Как уже отмечалось, при использовании этой стратегии необходимо сравнить выходные реакции для всевозможных пар состояний 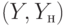 исправной и неисправной схем. Эта процедура требует значительных вычислительных ресурсов при длинных входных последовательностях для схем, содержащих большое число элементов памяти.
исправной и неисправной схем. Эта процедура требует значительных вычислительных ресурсов при длинных входных последовательностях для схем, содержащих большое число элементов памяти.
Известно, что троичное моделирование не позволяет точно оценить полноту теста [24.1], поэтому последнее время все чаще используется символьное моделирование логических схем. Символьное моделирование, в отличие от обычно применяемого логического моделирования в троичном алфавите, позволяет получить точные значения сигналов для каждой линии схемы для заданной входной последовательности 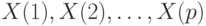 и неопределенного начального состояния схемы.
При этом каждому
и неопределенного начального состояния схемы.
При этом каждому  -ому элементу памяти ставится в соответствие переменная состояния
-ому элементу памяти ставится в соответствие переменная состояния  . Тогда состояние исправной схемы описывается вектором переменных
. Тогда состояние исправной схемы описывается вектором переменных 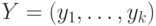 , где
, где 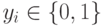 для
для  . В процессе символьного моделирования для каждой линии схемы строится булева функция, которая зависит от переменных состояний
. В процессе символьного моделирования для каждой линии схемы строится булева функция, которая зависит от переменных состояний 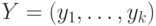 .
.
Для заданной входной последовательности  сначала выполняется символьное моделирование исправной схемы, которое определяет для каждой линии булевы выражения, определяющие зависимость от переменных состояний.
Далее для каждой отобранной неисправности (обычно тех, которые не обнаруживаются с использованием троичного моделирования) для каждого временного такта
сначала выполняется символьное моделирование исправной схемы, которое определяет для каждой линии булевы выражения, определяющие зависимость от переменных состояний.
Далее для каждой отобранной неисправности (обычно тех, которые не обнаруживаются с использованием троичного моделирования) для каждого временного такта  и
и  -го выхода определяются символьные выражения выхода
-го выхода определяются символьные выражения выхода 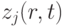 , где
, где  -состояние исправной схемы.
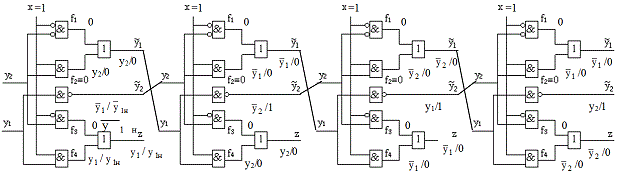
Для нашего примера из предыдущего раздела на рис. 24.1 представлены результаты символьного моделирования исправной и неисправной схемы (рис. 22.1) для входной последовательности
-состояние исправной схемы.
Для нашего примера из предыдущего раздела на рис. 24.1 представлены результаты символьного моделирования исправной и неисправной схемы (рис. 22.1) для входной последовательности  . Здесь, для каждой линии схемы получены булевы выражения в терминах переменных состояний
. Здесь, для каждой линии схемы получены булевы выражения в терминах переменных состояний 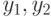 исправной и в терминах
исправной и в терминах 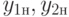 неисправной схемы.
неисправной схемы.
увеличить изображение
Рис. 24.1. Итеративная комбинационная схема с данными символьного моделирования
24.3 Дизъюнктивная форма различающей функции для последовательностных схем
Как уже говорилось выше, элегантным методом решения проблемы построения теста является использование математического аппарата различающих функций, который обобщает понятие различающей функции (24.1), (24.2) для комбинационных схем на схемы с памятью. Согласно [24.1,24.2] определим различающую функцию 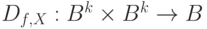 в случае применения стратегии кратного наблюдения для каждой неисправности
в случае применения стратегии кратного наблюдения для каждой неисправности  и входной последовательности
и входной последовательности 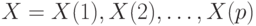 следующим образом:
следующим образом:
![D^{МОТ}_{f,X}=\bigvee\limits_{t=1}^{p}{\bigvee\limits_{j=1}^{m}
{[z_j(X,Y,t)\oplus z_j^f(X,Y_н,t)]}}](/sites/default/files/tex_cache/3299658964d9b7ffae062df9d11b2794.png) |
( 24.7) |
При этом 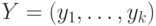 и
и
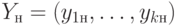 обозначают переменные состояний, представляющих начальные состояния исправной
обозначают переменные состояний, представляющих начальные состояния исправной
 и неисправной
и неисправной  схем. Данная различающая функция сравнивает все выходные последовательности исправной и неисправной схем для моментов времени
схем. Данная различающая функция сравнивает все выходные последовательности исправной и неисправной схем для моментов времени 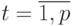 одновременно.
одновременно.
Моделирование неисправных схем с применением стратегии кратного наблюдения выполняется с помощью символьного моделирования с итеративным вычислением различающих функций 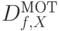 .
С целью выполнения этой процедуры для каждой неисправности вводится вспомогательная (текущая) различающая функция
.
С целью выполнения этой процедуры для каждой неисправности вводится вспомогательная (текущая) различающая функция
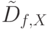 , которая при инициализации получает нулевое значение. Далее в процессе символьного моделирования к ней последовательно добавляется на каждом шаге дизъюнктивный терм, соответствующий своему моменту времени
, которая при инициализации получает нулевое значение. Далее в процессе символьного моделирования к ней последовательно добавляется на каждом шаге дизъюнктивный терм, соответствующий своему моменту времени
![\tilde{D}_{f,X}(Y,Y_н)\gets\tilde{D}_{f,X}(Y,Y_н)\vee (\bigvee\limits_{j=1}^{m}{[z_j(Y,t)\oplus z_j^f(Y_н,t)]}).](/sites/default/files/tex_cache/c1f72b4190682519e50753f37dcacb66.png)
При достижении в процессе моделирования внешнего выхода  выполняется проверка обнаружимости рассматриваемой неисправности относительно используемой стратегии наблюдения выходных сигналов.
выполняется проверка обнаружимости рассматриваемой неисправности относительно используемой стратегии наблюдения выходных сигналов.
Можно показать [24.1,24.2], что неисправность  является обнаружимой относительно стратегии кратного наблюдения, если и только если
является обнаружимой относительно стратегии кратного наблюдения, если и только если 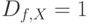 для данной входной последовательности
для данной входной последовательности  . Равенство
. Равенство 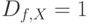 говорит о том, что различающая функция содержит все пары состояний исправной и неисправной схемы (все пары состояний различаются последовательностью
говорит о том, что различающая функция содержит все пары состояний исправной и неисправной схемы (все пары состояний различаются последовательностью  ). Если
). Если 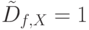 , то неисправность отмечается как обнаруженная и исключается из дальнейшего рассмотрения. Следует отметить, что оценка полноты входной тестовой последовательности также может быть выполнена путем сравнения выходных реакций с символьными выражениями соответствующих выходов схемы.
, то неисправность отмечается как обнаруженная и исключается из дальнейшего рассмотрения. Следует отметить, что оценка полноты входной тестовой последовательности также может быть выполнена путем сравнения выходных реакций с символьными выражениями соответствующих выходов схемы.
Для нашего примера (входной последовательности  схемы (рис. 22.1) для первого такта имеем
схемы (рис. 22.1) для первого такта имеем
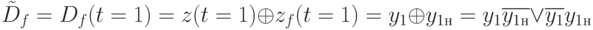
Для второго такта имеем
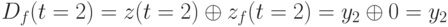 ,
что дает
,
что дает

Для третьего такта получаем
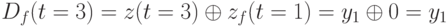 ,
,
откуда следует
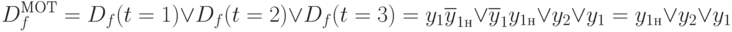
Наконец для 4-го такта получаем 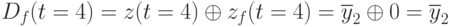 , что ведет к
, что ведет к
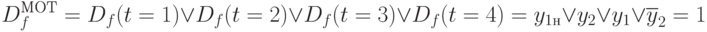
Покажем соответствие полученных выражений узлам обратного различающего дерева рис. 22.3. Возьмем правый узел первого уровня ОРД 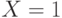 , которому соответствуют множества неразличимых пар состояний
, которому соответствуют множества неразличимых пар состояний 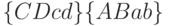 исправной и неисправной схемы.
Очевидно, что состояния, содержащиеся в разных
исправной и неисправной схемы.
Очевидно, что состояния, содержащиеся в разных  -множествах
-множествах  , различаются входной последовательностью
, различаются входной последовательностью 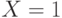 . Получаем следующие различаемые пары состояний для нашего примера:
. Получаем следующие различаемые пары состояний для нашего примера: 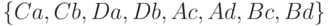 . Можно показать, что каждой различимой паре состояний исправной и неисправной схемы соответствует терм совершенной дизъюнктивной нормальной формы (СДНФ):
. Можно показать, что каждой различимой паре состояний исправной и неисправной схемы соответствует терм совершенной дизъюнктивной нормальной формы (СДНФ):
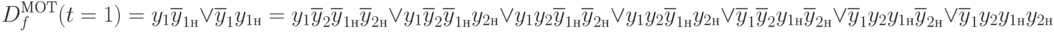
Например, первый терм
 соответствует различимой паре
соответствует различимой паре  последний терм
последний терм
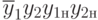 - паре
- паре 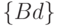 .
Аналогично правый узел второго уровня ОРД
.
Аналогично правый узел второго уровня ОРД  соответствует
соответствует
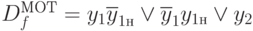 . Если мы разложим это выражение в СДНФ, то обнаружим соответствие каждой различимой пары терму СДНФ. Таким же образом правому узлу третьего уровня ОРД
. Если мы разложим это выражение в СДНФ, то обнаружим соответствие каждой различимой пары терму СДНФ. Таким же образом правому узлу третьего уровня ОРД  соответствует
соответствует 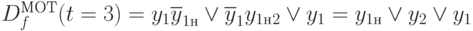 и узлу четвертого уровня
и узлу четвертого уровня  - соответствует
- соответствует 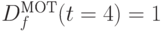 .
.
Равенство РФ  говорит о том, что различающая функция содержит все пары состояний исправной и неисправной схемы и поэтому неисправность
говорит о том, что различающая функция содержит все пары состояний исправной и неисправной схемы и поэтому неисправность 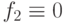 схемы рис. 22.1 проверяется входной последовательностью
схемы рис. 22.1 проверяется входной последовательностью  относительно кратной стратегии наблюдения.
относительно кратной стратегии наблюдения.
Таким образом, поиск пути на ОРД, соответствующего тестовой последовательностью можно выполнить с помощью символьного моделирования и вычисления различающей функции. Поиск тестовой последовательности 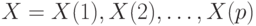 сводится к решению булева уравнения
сводится к решению булева уравнения  . Фактически дизъюнктивная форма различающей функции позволяет свести задачу построения проверяющей последовательности для заданной неисправности схемы с памятью к проверке тавтологии
. Фактически дизъюнктивная форма различающей функции позволяет свести задачу построения проверяющей последовательности для заданной неисправности схемы с памятью к проверке тавтологии  .
Быстродействие современной вычислительной техники наряду с развитой техникой символьных вычислений [24.6] позволяет применять этот подход для реальных последовательностных схем.
.
Быстродействие современной вычислительной техники наряду с развитой техникой символьных вычислений [24.6] позволяет применять этот подход для реальных последовательностных схем.
Решение уравнения  можно реализовать различными способами, в частности, с помощью генетических алгоритмов (ГА) [24.1].
Если провести аналогию с обратным различающим деревом, то в данном случае генетический алгоритм должен выбрать самый перспективный двоичный набор (вершину нижнего уровня ОРД), который следует добавить к текущей тестовой последовательности. Заметим, что в этом случае потенциальным решением является один входной набор, а не вся тестовая последовательность, что, как правило, имеет место при использовании ГА в структурном построении тестов для последовательностных схем [24.1].
Это позволяет снизить размерность этой (локальной) задачи. Поскольку целью генерации тестовой последовательности в этом случае является
можно реализовать различными способами, в частности, с помощью генетических алгоритмов (ГА) [24.1].
Если провести аналогию с обратным различающим деревом, то в данном случае генетический алгоритм должен выбрать самый перспективный двоичный набор (вершину нижнего уровня ОРД), который следует добавить к текущей тестовой последовательности. Заметим, что в этом случае потенциальным решением является один входной набор, а не вся тестовая последовательность, что, как правило, имеет место при использовании ГА в структурном построении тестов для последовательностных схем [24.1].
Это позволяет снизить размерность этой (локальной) задачи. Поскольку целью генерации тестовой последовательности в этом случае является  , то в генетическом алгоритме для оценки потенциальных решений (входных последовательностей) следует использовать фитнесс-функцию, которая определяет близость различающей функции для анализируемой входной последовательности к значению 1 (
, то в генетическом алгоритме для оценки потенциальных решений (входных последовательностей) следует использовать фитнесс-функцию, которая определяет близость различающей функции для анализируемой входной последовательности к значению 1 ( ). Заметим, что чем больше пар состояний исправной и неисправной схем различается, тем ближе различающая функция к 1.
Поэтому можно взять различающую функцию вида
). Заметим, что чем больше пар состояний исправной и неисправной схем различается, тем ближе различающая функция к 1.
Поэтому можно взять различающую функцию вида 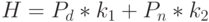 , где
, где 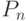 определяется числом вновь различенных пар состояний исправной и неисправной схем, а
определяется числом вновь различенных пар состояний исправной и неисправной схем, а 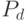 определяется числом пар состояний, различенных на предыдущих входных наборах. Здесь
определяется числом пар состояний, различенных на предыдущих входных наборах. Здесь 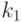 и
и 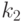 - весовые коэффициенты
- весовые коэффициенты 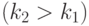 . Заметим, что в этом случае можно использовать стандартные генетические операторы кроссинговера и мутации [24.1].
. Заметим, что в этом случае можно использовать стандартные генетические операторы кроссинговера и мутации [24.1].