|
Добрый день можно поинтересоваться где брать литературу предложенную в курсе ?Большинство книг я не могу найти в известных источниках |
Многомерная активизация путей в шестизначном алфавите
18.1 Шестизначный алфавит в генерации тестов
Булевы функции в двузначном алфавите 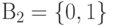 широко используются для моделирования исправных комбинационных схем, но для описания работы схемы с неисправностью удобно использовать алфавиты большей значности [18.1]. В этом случае анализ двух схем (исправной и неисправной) в двоичном алфавите заменяется анализом одной схемы в многозначном алфавите. При поданном некотором тестовом наборе для каждой линии в исправной и неисправной схеме возможны четыре комбинации значений сигналов:
широко используются для моделирования исправных комбинационных схем, но для описания работы схемы с неисправностью удобно использовать алфавиты большей значности [18.1]. В этом случае анализ двух схем (исправной и неисправной) в двоичном алфавите заменяется анализом одной схемы в многозначном алфавите. При поданном некотором тестовом наборе для каждой линии в исправной и неисправной схеме возможны четыре комбинации значений сигналов:
00 - 0 в исправной схеме, и 0 в неисправной (соответствует символу 0 универсального алфавита 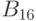 , рассмотренного в
"Система многозначных алфавитов и функций"
);
, рассмотренного в
"Система многозначных алфавитов и функций"
);
11 - 1 в исправной схеме и 1 в неисправной (символ 1 алфавита 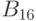 );
);
10 - 1 в исправной схеме и 0 в неисправной (символ  алфавита
алфавита 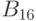 );
);
01 - 0 в исправной схеме и 1 в неисправной (символ 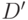 алфавита
алфавита 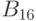 );
);
Мы не знаем, какие именно из этих четырёх комбинаций могут присутствовать для данной неисправности, поэтому в начале построения теста предполагается, что на каждой линии схемы возможны все 4 комбинации - максимально возможная неопределённость. Суть методов генерации тестов в многозначных алфавитах заключается в том, что, используя свойства структуры схемы и знания местоположения неисправностей далее, исключаются ненужные или невозможные комбинации [18.1]. То есть, в процессе генерации тестов неопределённость постепенно снимается и значения 0, 1 на внешних входах схемы, которые получаются в результате снятия неопределённости, определяют проверяющий тест для данной неисправности. При снятии неопределённости для произвольной линии схемы возможны различные ситуации, описываемые универсальным 16-значным алфавитом  . Таким образом, в начале построения теста всем линиям схемы присваивается неопределённое значение
. Таким образом, в начале построения теста всем линиям схемы присваивается неопределённое значение  алфавита
алфавита  , а далее эта неопределённость постепенно снимается. Например, если мы строим тест для константы неисправности
, а далее эта неопределённость постепенно снимается. Например, если мы строим тест для константы неисправности  , то, очевидно, что этой линии надо присвоить значение
, то, очевидно, что этой линии надо присвоить значение  из
из  , а в случае неисправности
, а в случае неисправности 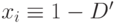 . Затем эти значения стараются распространить к внешнему выходу схемы, чтобы обеспечить наблюдение влияния неисправностей на внешнем выходе. При этом снимается неопределённость для линий, попавших в активизированные пути и получивших, например, значение
. Затем эти значения стараются распространить к внешнему выходу схемы, чтобы обеспечить наблюдение влияния неисправностей на внешнем выходе. При этом снимается неопределённость для линий, попавших в активизированные пути и получивших, например, значение  или
или 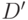 . Этот процесс является аналогом прямой фазы активизации одномерных путей. Далее надо отработать назад к внешним входам схемы, чтобы обеспечить условие активизации путей. Этот процесс является аналогом обратной фазы метода активизации одномерных путей. При этом также снимается неопределённость.
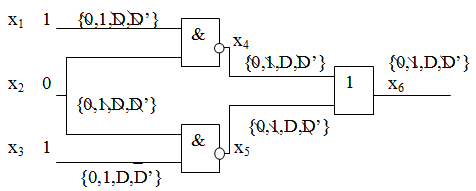
алРезультаты этого процесса для неисправности представлены на рис. 18.1.
. Этот процесс является аналогом прямой фазы активизации одномерных путей. Далее надо отработать назад к внешним входам схемы, чтобы обеспечить условие активизации путей. Этот процесс является аналогом обратной фазы метода активизации одномерных путей. При этом также снимается неопределённость.
алРезультаты этого процесса для неисправности представлены на рис. 18.1.
Различные методы генерации тестов используют разные подмножества универсального алфавита 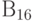 [18.1].
Наименьшим подмножеством
[18.1].
Наименьшим подмножеством  , которое используется в распространенных на практике методах генерации тестов, является алфавит
, которое используется в распространенных на практике методах генерации тестов, является алфавит  . Здесь символы
. Здесь символы  и
и 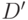 представляют рассогласование сигналов в исправной и неисправной схемах и фактически показывают влияние данной неисправности в схеме.
Символы 0,1 представляют одинаковые значения сигналов в исправной и неисправной схемах. Символ
представляют рассогласование сигналов в исправной и неисправной схемах и фактически показывают влияние данной неисправности в схеме.
Символы 0,1 представляют одинаковые значения сигналов в исправной и неисправной схемах. Символ  соответствует неопределенным значения в исправной и неисправной схемах. Наконец, символ \varnothing используется для описания конфликтов (противоречия сигналов), которые могут быть в процессе построения тестов.
соответствует неопределенным значения в исправной и неисправной схемах. Наконец, символ \varnothing используется для описания конфликтов (противоречия сигналов), которые могут быть в процессе построения тестов.
Во всех структурных методах, использующих многозначные алфавиты, выполняются следующие основные этапы, которые обобщают соответствующие этапы метода одномерной активизации путей [18.1,18.2].
- Активизация (sensitization) данной неисправности. При этом вносится влияние данной неисправности на соответствующей линии путем присваивания ей значения
 (для неисправности const0) или
(для неисправности const0) или 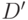 (для неисправности const1).
(для неисправности const1).
- D-распространение (D-propagation), при котором значения
 или
или 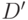 распространяются до одного из внешних выходов схемы. Эта процедура обеспечивает наблюдение влияния неисправности на внешних выходах.
распространяются до одного из внешних выходов схемы. Эта процедура обеспечивает наблюдение влияния неисправности на внешних выходах.
- Доопределение (justification), при котором определяются значения внешних входов схемы, обеспечивающих значения, получаемые на этапах (1) и (2).
- Импликация, которая используется для снятия неопределённости на линиях схемы, которые возможны в результате присваивания некоторым линиям определённых значений.
При выполнении D-распространения в случае разветвления есть выбор возможных путей от места неисправностей к внешним выходам. Множество элементов, для которых возможно D-распространение называются D-границей (элементы имеют значения  или
или 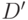 на входе и неопределенность
на входе и неопределенность  на выходе).
на выходе).
Аналогично при выполнении этапа доопределения (justification) также возможен выбор различных вариантов продвижения к внешним входам. Множество элементов, у которых выходное значение определено (имеют значения 0 или 1), но не подтверждается входными значениями (входы имеют неопределенные значения  ) называется J-границей.
) называется J-границей.
Так как при генерации тестов мы используем не двоичные, а многозначные алфавиты, функционирование логических элементов также должно быть описано в многозначном алфавите. Часто это делается с помощью специальных таблиц такого же типа, как и при моделировании многозначных алфавитов, которые были представлены в разделах 2 и 3. Например, в табл. 18.1 - 18. представлены модели основных вентилей в алфавите  . Следует отметить, что различные методы генерации тестов могут использовать не только разные подмножества универсального многозначного алфавита
. Следует отметить, что различные методы генерации тестов могут использовать не только разные подмножества универсального многозначного алфавита  , но и различные формы многозначных моделей, которые мы рассмотрим далее.
, но и различные формы многозначных моделей, которые мы рассмотрим далее.
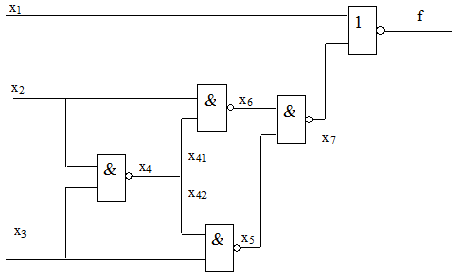
Процедура импликации используется для максимально возможного снятия неопределенности на линиях схемы, которое возможно вследствие присваивания некоторым линиям определенных значений (как на этапе D-распространения, так и на этапе доопределения). Например, если в схеме рис. 18.2 установить значение 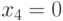 , то из этого, очевидно, следует, что сигналы
, то из этого, очевидно, следует, что сигналы 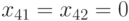 . Из равенства
. Из равенства 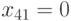 следует однозначно
следует однозначно  .
Аналогично
.
Аналогично 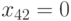 имплицирует
имплицирует 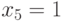 . Кроме этого, из равенства
. Кроме этого, из равенства  однозначно следует равенства
однозначно следует равенства  ,
, 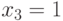 .
.
Различают прямую и обратную импликацию. При прямой импликации снимается неопределенность на линиях элементов - последователей данной линии (для нашего примера 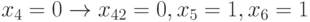 ). Обратная импликация снимает неопределенность у линий, являющихся предшественниками данной линии (для нашего примера
). Обратная импликация снимает неопределенность у линий, являющихся предшественниками данной линии (для нашего примера 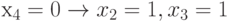 ).
).
Прямая импликация фактически сводится к логическому моделированию в алфавите  фрагмента схемы, последователей линии с изменившимся сигналом. Это может быть выполнено, например, с помощью табличных многозначных моделей, приведенных в табл. 18.1-18.4.
фрагмента схемы, последователей линии с изменившимся сигналом. Это может быть выполнено, например, с помощью табличных многозначных моделей, приведенных в табл. 18.1-18.4.
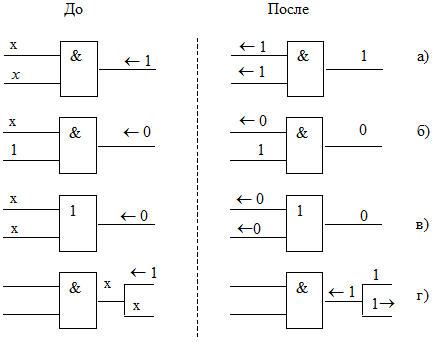
Типовые ситуации, где может быть выполнена обратная импликация, представлены на рис. 18.3.