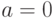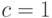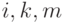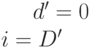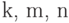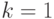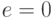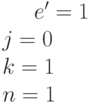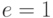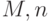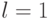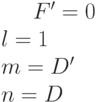|
Добрый день можно поинтересоваться где брать литературу предложенную в курсе ?Большинство книг я не могу найти в известных источниках |
Методы генерации тестов PODEM, FAN и SOCRATES
19.1 Метод PODEM
Как и D-алгоритм, метод PODEM (path-oriented decision making) использует тот же шестизначный алфавит
 , но в нем применяется другая стратегия поиска тестового набора [19.1]. Отметим, что целью любого алгоритма построения теста для данной неисправности является входной двоичный вектор, который проверяет эту неисправность. Таким образом, искомый тест принадлежит пространству всевозможных двоичных входных наборов. Но пространством поиска в D-алгоритме является множество всевозможных (в том числе и кратных)
, но в нем применяется другая стратегия поиска тестового набора [19.1]. Отметим, что целью любого алгоритма построения теста для данной неисправности является входной двоичный вектор, который проверяет эту неисправность. Таким образом, искомый тест принадлежит пространству всевозможных двоичных входных наборов. Но пространством поиска в D-алгоритме является множество всевозможных (в том числе и кратных) 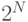 путей в схеме от места неисправности до какого либо внешнего выхода, где
путей в схеме от места неисправности до какого либо внешнего выхода, где  - число элементов. В методе PODEM пространством поиска является непосредственно множество всевозможных входных наборов, мощность которого
- число элементов. В методе PODEM пространством поиска является непосредственно множество всевозможных входных наборов, мощность которого  обычно меньше
обычно меньше 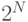 , поскольку, как правило,
, поскольку, как правило,  . Это позволяет существенно ускорить процесс поиска.
. Это позволяет существенно ускорить процесс поиска.
Основные отличия метода PODEM от D-алгоритма следующие:
- другая процедура D-распространения;
- отличная процедура доопределения;
- выполняется только прямая импликация (от внешних входов к выходам);
- иная стратегия поиска решения и обработки противоречивых ситуаций.
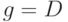
D-распространение в методе РОДЕМ выполняется пошагово. В D-границе выбирается в качестве "цели" наиболее перспективный элемент (ближайший к внешнему выходу или имеющий лучший показатель наблюдаемости) и затем сразу с помощью других процедур (в первую очередь процедуры продвижения назад) находится входной набор, обеспечивающий достижение поставленной локальной цели - D-распространения через данный элемент. Напомним, что в D-алгоритме D-распространение выполняется до внешнего выхода, а затем производится доопределение.
Алгоритм выбора цели для константной неисправности вентиля  представлен псевдокодом рис. 19.1.
представлен псевдокодом рис. 19.1.
Здесь выбор элемента в D-границе производится по лучшему показателю наблюдаемости (в простейшем случае выбирается элемент, ближайший к одному из внешних выходов).
Доопределение производится с помощью двух основных процедур - распространения назад и импликации. Эффективность метода РОДЕМ во многом определяется процедурой продвижения назад. Поскольку метод разработан для схем, описанных на уровне простейших вентилей И, ИЛИ, НЕ, НЕ-И, НЕ-ИЛИ, то процедура достаточно проста. Начиная с элемента, выбранного в качестве "цели", по мере продвижения к внешним входам, процедура для каждого вентиля по заданному значению одного выхода определяет значение только одного входа. Ее результатом является присваивание определенного значения (0 или 1) одному внешнему входу схемы в результате прохождения одного пути от "целевого элемента" до этого внешнего входа.
Пусть целью процедуры является установка значения  на линии
на линии  . Тогда значение внешнего входа определяется четностью числа элементов инвертирующего типа
. Тогда значение внешнего входа определяется четностью числа элементов инвертирующего типа  вдоль выбранного пути (при прохождении через элементы НЕ, НЕ-И, НЕ-ИЛИ значение сигнала инвертируется). Процедура продвижения назад для внутренней линии
вдоль выбранного пути (при прохождении через элементы НЕ, НЕ-И, НЕ-ИЛИ значение сигнала инвертируется). Процедура продвижения назад для внутренней линии  находит внешний вход
находит внешний вход 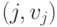 .
При этом
.
При этом 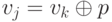 , где
, где  - четность пути от
- четность пути от  до
до  . Следует отметить, что значение присваивается только одному внешнему входу. Внутренние линии сохраняют при этом свои старые значения (как правило, неопределенные значения -
. Следует отметить, что значение присваивается только одному внешнему входу. Внутренние линии сохраняют при этом свои старые значения (как правило, неопределенные значения -  ). Псевдокод процедуры продвижения назад представлен на рис. 19.2.
). Псевдокод процедуры продвижения назад представлен на рис. 19.2.
Особо следует отметить правила выбора входа элемента. Здесь, прежде всего, определяется: имеется ли один или несколько вариантов присваивания значений входов вентиля, при которых на его выходе устанавливается требуемое значение. В случае нескольких вариантов (например, 0 на выходе вентиля И может быть получен в результате установки 0 на любом входе; аналогично 1 на выходе вентиля ИЛИ можно получить присваиванием 1 любому из его входов) выбирается вход элемента, ближайший к внешнему входу или имеющий лучший показатель управляемости. То есть в этом случае мы выбираем наиболее перспективный путь. Если имеется только один вариант (например, 0 на выходе вентиля ИЛИ может быть получен только установкой всех его входов в 0; соответственно 1 на выходе вентиля И - установкой всех входов в 1), то выбирается вход, наиболее далекий от внешних входов или имеющий худший показатель управляемости. Это делается с целью скорейшего обнаружения противоречивой ситуации, если она возможна вследствие данного присваивания.
После того, как внешний вход в результате этой процедуры получил определенное значение, выполняется прямая импликация путем моделирования в алфавите  . Если в результате импликации цель достигнута, то выполняется следующий шаг D-распространения. В противном случае, выполняется процедура продвижения назад для элементов записанных в стек на предыдущем шаге, до тех пор, пока не будет достигнута цель. Прямая импликация выполняется путем моделирования в алфавите
. Если в результате импликации цель достигнута, то выполняется следующий шаг D-распространения. В противном случае, выполняется процедура продвижения назад для элементов записанных в стек на предыдущем шаге, до тех пор, пока не будет достигнута цель. Прямая импликация выполняется путем моделирования в алфавите 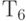 , как правило, с помощью таблиц для вентилей, представленных в табл. 18.1-4, от внешних входов к выходам.
, как правило, с помощью таблиц для вентилей, представленных в табл. 18.1-4, от внешних входов к выходам.
В случае возникновения противоречия на этапе импликации начинается перебор значений внешних входов, получивших к этому моменту определенные значения. После выполнения процедуры продвижения назад каждое вновь полученное двоичное значение внешнего входа заносится в стек.
В случае возникновения противоречия значение внешнего входа, записанного в стек последним, меняется на противоположное. Далее снова выполняется импликация. Если и в этом случае возникает противоречие, то меняется на противоположное значение следующего внешнего входа в стеке. Процесс поиска прекращается, если цель достигнута или все варианты исчерпаны (теста не существует). На рис. 19.3 представлен псевдокод алгоритма, реализующего метод РОDЕМ.
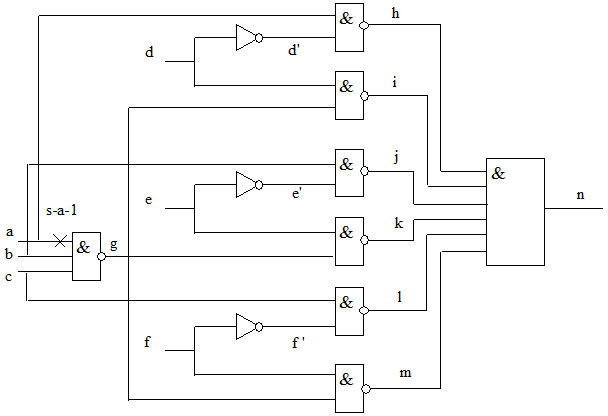
В качестве примера рассмотрим построение теста для неисправности
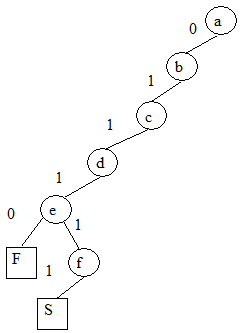
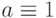 в схеме рис. 19.4. В табл. 19.1 показаны результаты основных этапов генерации теста для этой неисправности. Здесь для каждого этапа приведены значения цели, внешних входов, состояние D-границы. Соответственно на рис. 19.5 показано дерево решений для этого примера. Поскольку при поиске тестового набора решение заключается в выборе одного из двух двоичных значений) 0,1 для внешнего входа, то дерево является двоичным. Здесь каждый узел соответствует внешнему входу, который принимает двоичное значение при построении теста;
в схеме рис. 19.4. В табл. 19.1 показаны результаты основных этапов генерации теста для этой неисправности. Здесь для каждого этапа приведены значения цели, внешних входов, состояние D-границы. Соответственно на рис. 19.5 показано дерево решений для этого примера. Поскольку при поиске тестового набора решение заключается в выборе одного из двух двоичных значений) 0,1 для внешнего входа, то дерево является двоичным. Здесь каждый узел соответствует внешнему входу, который принимает двоичное значение при построении теста;  и
и  (в квадрате) - соответственно успех и неудачу при данном выборе.
(в квадрате) - соответственно успех и неудачу при данном выборе.
Метод РОDЕМ существенно проще в программной реализации, чем D-алгоритм и доказал свою эффективность для больших комбинационных ДУ (объемом до нескольких десятков тысяч вентилей).