|
Добрый день можно поинтересоваться где брать литературу предложенную в курсе ?Большинство книг я не могу найти в известных источниках |
Сокращение диагностической информации при помощи масок
В работе [1] рассматривается еще один возможный способ организация словаря неисправностей, в котором для каждого технического состояния сохраняется часть полной реакции устройства в этом состоянии на диагностический тест, выделенная с помощью некоторого шаблона, который именуется маской.
Назовем точкой проверки пару номер тестового воздействия:номер выхода. Тогда маской  назовем любую совокупность точек проверки.
назовем любую совокупность точек проверки.
Пусть имеется некоторое разбиение множества  и пусть
и пусть 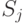 - элементы этого разбиения.
Поставим в соответствие каждому подмножеству
- элементы этого разбиения.
Поставим в соответствие каждому подмножеству 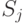 некоторую маску
некоторую маску 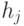 . Множество всех
. Множество всех 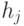 обозначим через
обозначим через  . Построим по списку полных реакций (СПР) и множеству масок
. Построим по списку полных реакций (СПР) и множеству масок  таблицу следующим образом. Каждая строка таблицы соответствует техническому состоянию.
Содержимое строки таблицы, соответствующей состоянию
таблицу следующим образом. Каждая строка таблицы соответствует техническому состоянию.
Содержимое строки таблицы, соответствующей состоянию 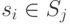 , будут составлять значения точек проверки из
, будут составлять значения точек проверки из 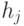 , взятые из строки СПР, соответствующей
, взятые из строки СПР, соответствующей  , в порядке их следования в СПР. Построенную таким образом таблицу будем называть (по аналогии с [1]) словарем полной реакции, построенный по маскам из
, в порядке их следования в СПР. Построенную таким образом таблицу будем называть (по аналогии с [1]) словарем полной реакции, построенный по маскам из  , и обозначать
, и обозначать 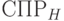 .
Маску
.
Маску 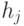 будем называть индивидуальной маской для каждого состояния из
будем называть индивидуальной маской для каждого состояния из 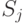 , а множество
, а множество  - множеством индивидуальных масок.
- множеством индивидуальных масок.
Например, построим СПР для СПР из табл. 27.5, если
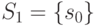 ,
,
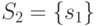 ,
,
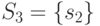 ,
,
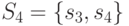 ,
,
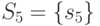 ,
,
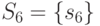 ,
,
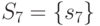 ,
,
 ,
а элементы множества
,
а элементы множества  :
:
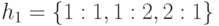 ,
,
 ,
,
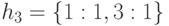 ,
,
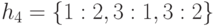 ,
,
 ,
,
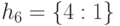 ,
,
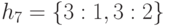 ,
,
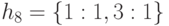 .
Элементы СПР, выбираемые с помощью масок из
.
Элементы СПР, выбираемые с помощью масок из  , выделены прямоугольниками в СПР в табл. 29.1, а сам словарь неисправностей
, выделены прямоугольниками в СПР в табл. 29.1, а сам словарь неисправностей 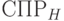 приведен в табл. 29.2.
приведен в табл. 29.2.
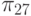 |
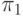 |
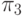 |
 |
|
|---|---|---|---|---|
 |
11 | 00 | 11 | 10 |
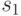 |
10 | 10 | 11 | 10 |
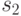 |
00 | 00 | 11 | 10 |
 |
00 | 00 | 00 | 10 |
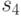 |
01 | 00 | 00 | 10 |
 |
01 | 00 | 01 | 10 |
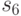 |
01 | 00 | 01 | 00 |
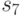 |
10 | 00 | 10 | 10 |
 |
11 | 11 | 11 | 10 |
Заметим, что представление диагностической информации в виде 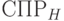 предполагает наличие полной таблицы СПР, а также множества масок
предполагает наличие полной таблицы СПР, а также множества масок  и указания соответствия между
и указания соответствия между  и
и 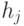 .
.
Содержательно выделение информации с помощью маски можно пояснить следующим образом. Полную СПР будем интерпретировать как прямоугольную таблицу с пронумерованными строками и столбцами. В каждой клетке СПР, находящейся на пересечении  -ой строки и
-ой строки и  -го столбца, находится двоичная последовательность длины
-го столбца, находится двоичная последовательность длины  , где
, где  - число выходов диагностируемого ЦУ.Эта последовательность есть реакция ЦУ в состоянии
- число выходов диагностируемого ЦУ.Эта последовательность есть реакция ЦУ в состоянии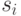 на
на  -ый тестовый набор.
Тогда маска
-ый тестовый набор.
Тогда маска  соответствует "окошечкам" в сплошном битовом шаблоне
соответствует "окошечкам" в сплошном битовом шаблоне  -ой строки, которые следует "прорезать" , чтобы увидеть выделяемые этой маской биты реакции ЦУ на диагностический тест.
-ой строки, которые следует "прорезать" , чтобы увидеть выделяемые этой маской биты реакции ЦУ на диагностический тест.
В процессе диагностирования предполагается получение выходной реакции объекта диагностирования на диагностический тест, после чего на эту реакцию накладываются поочередно маски 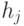 , а результат наложения сравнивается со значениями в
, а результат наложения сравнивается со значениями в 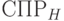 для всех
для всех 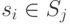 . Те из
. Те из  , для которых произошло совпадение, заносятся в СПН.
, для которых произошло совпадение, заносятся в СПН.
Пусть в рассматриваемом примере объект находится в техническом состоянии 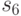 . В этом случае выходная реакция объекта -
. В этом случае выходная реакция объекта - 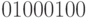 . Ни одна из масок, кроме
. Ни одна из масок, кроме 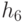 , не приведет к занесению в СПН ни одного состояния. После наложения маски
, не приведет к занесению в СПН ни одного состояния. После наложения маски 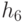 будет получена последовательность 0 и в СПН будет внесено состояние
будет получена последовательность 0 и в СПН будет внесено состояние 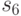 . Результат диагностирования объекта есть СПН, равный
. Результат диагностирования объекта есть СПН, равный  .
.
Очевидно, что если СПР обладает свойством различения всех неисправностей, то найдется множество индивидуальных масок таких, что 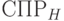 будет обладать свойством различения всех неисправностей.
будет обладать свойством различения всех неисправностей.
Если множество  содержит только одну маску для всех технических состояний из
содержит только одну маску для всех технических состояний из  , то такую маску называют единой (общей) маской.
, то такую маску называют единой (общей) маской.
Рассмотрим, например, диагностический тест для схемы 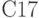 и множество
и множество  , содержащее одну маску
, содержащее одну маску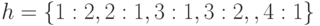 . В этом случае
. В этом случае 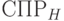 будет выглядеть так, как показано в табл. 29.3.
будет выглядеть так, как показано в табл. 29.3.
Использование единой маски имеет некоторые преимущества в процессе диагностирования объекта. Действительно, если используется единая маска , то при получении выходной реакции устройства можно сразу отфильтровывать с использованием маски  последовательность выходных значений и не сохранять при этом всю выходную реакцию. Более того, после получения очередного "отфильтрованного" с помощью маски выходного значения можно сразу формировать и вносить изменения в СПН. Сначала в СПН вносятся все технические состояния объекта, но при получении очередного бита информации происходит удаление из СПН состояний, не соответствующих значению данного бита.
последовательность выходных значений и не сохранять при этом всю выходную реакцию. Более того, после получения очередного "отфильтрованного" с помощью маски выходного значения можно сразу формировать и вносить изменения в СПН. Сначала в СПН вносятся все технические состояния объекта, но при получении очередного бита информации происходит удаление из СПН состояний, не соответствующих значению данного бита.
Что касается объема сокращенного с помощью масок словаря неисправностей, то в случае единой маски его величина равна 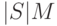 , где
, где  - количество точек проверок, составляющих маску. В случае сокращения ДИ с помощью множества индивидуальных масок объем словаря составит
- количество точек проверок, составляющих маску. В случае сокращения ДИ с помощью множества индивидуальных масок объем словаря составит
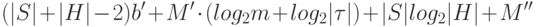
где 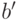 - количество бит, необходимых для отделения данных по одному техническому состоянию от остальной информации,
- количество бит, необходимых для отделения данных по одному техническому состоянию от остальной информации,
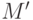 - суммарное количество точек проверки по всем маскам в множестве
- суммарное количество точек проверки по всем маскам в множестве  ,
,
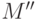 - суммарное количество точек проверки по всем маскам, с учетом их кратности.
- суммарное количество точек проверки по всем маскам, с учетом их кратности.
Заметим, что с помощью масок можно проводить сокращение ДИ, представленной также и в виде ТН.
В этом случае элементом маски  выступает не точка проверки, а номер тестового вектора, информация об обнаружении неисправности которого заносится в сокращенную таблицу.
Таблицу, построенную в результате сокращения ТН с помощью набора масок
выступает не точка проверки, а номер тестового вектора, информация об обнаружении неисправности которого заносится в сокращенную таблицу.
Таблицу, построенную в результате сокращения ТН с помощью набора масок  , будем называть таблицей неисправностей, построенной по маскам из
, будем называть таблицей неисправностей, построенной по маскам из  ,и обозначать через
,и обозначать через 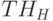 .
.
В связи со сказанным выше, подход к сокращению ДИ при помощи масок приводит к необходимости исследования задач поиска различных масок. Остановимся на этом немного подробнее.
Так, в работе [1] формулируются три задачи, касающиеся сокращения ДИ с помощью масок:
- Для каждого технического состояния найти такую индивидуальную маску
 , чтобы объем СПР (
, чтобы объем СПР (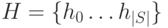 ,
,
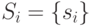 ) был минимальным и разрешающая способность диагностирования с помощью
) был минимальным и разрешающая способность диагностирования с помощью 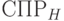 не ухудшалась по сравнению с разрешающей способностью диагностирования с помощью СПР.
не ухудшалась по сравнению с разрешающей способностью диагностирования с помощью СПР.
- Для множества технических состояний
 найти такую единую (общую) маску
найти такую единую (общую) маску  , чтобы объем
, чтобы объем 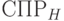 (
(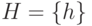 ) был минимальным и разрешающая способность диагностирования с помощью
) был минимальным и разрешающая способность диагностирования с помощью 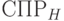 не ухудшалась по сравнению с разрешающей способностью диагностирования с помощью СПР.
не ухудшалась по сравнению с разрешающей способностью диагностирования с помощью СПР.
- Для множества состояний
 определить такое его разбиение
определить такое его разбиение 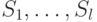 и такой набор масок
и такой набор масок 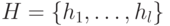 , чтобы объем
, чтобы объем 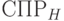 был минимальным и разрешающая способность диагностирования с помощью СПР не ухудшалась по сравнению с разрешающей способностью диагностирования с помощью СПР.
был минимальным и разрешающая способность диагностирования с помощью СПР не ухудшалась по сравнению с разрешающей способностью диагностирования с помощью СПР.
Сформулированные задачи принято называть задачами минимизации ДИ при помощи масок [2,3]. В работах [3,4,5,6] рассматриваются методы точного аналитического решения первой, а в работе [6] еще и второй из сформулированных задач.
В ряде случаев для решения задач минимизации применимы методы, предложенные для оптимизации безусловных алгоритмов диагностирования [7].
В работе [3] сформулирована еще одна задача - задача оптимизации: для множества  определить разбиение
определить разбиение 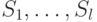 и набор масок
и набор масок 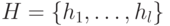 , чтобы объем
, чтобы объем 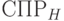 не превышал заданной величины
не превышал заданной величины  и изменение разрешающей способности диагностирования с помощью
и изменение разрешающей способности диагностирования с помощью 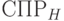 по отношению к разрешающей способности диагностирования с использованием СПР было минимальным. Здесь же рассматриваются варианты точного аналитического решения этой задачи.
по отношению к разрешающей способности диагностирования с использованием СПР было минимальным. Здесь же рассматриваются варианты точного аналитического решения этой задачи.
В работах [3,8] отмечается, что предложенные варианты точных решений задач поиска масок связаны с частичным перебором, и требуют большого объема вычислений. При значительном увеличении количества неисправных модификаций, характерного для современных устройств, а также при увеличении длины диагностического теста такие варианты решений становятся неприемлемыми из-за больших временных затрат. Выходом из сложившейся ситуации является замена точного решения приближенным. В тех же работах, а также в работе [2], предлагаются методы приближенного решения задачи минимизации и оптимизации объема 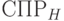 , когда
, когда  - множество индивидуальных масок.
- множество индивидуальных масок.
Каждый из упомянутых выше методов минимизации и оптимизации объема СПР имеет свои достоинства и недостатки и характеризуется определенной трудоемкостью. Следует заметить, что упомянутая трудоемкость для всех этих методов довольна велика и потому для ее сокращения требуются иные подходы.
Имеющийся опыт исследования многих оптимизационных прикладных задач показывает, что для их решения эффективным математическим аппаратом являются генетические алгоритмы (ГА). В лекции 25 была показана полезность ГА и их приемлемость с точки зрения временных затрат применительно к решению задач синтеза тестов. Далее мы убедимся, что и для различных модификаций задач поиска масок ГА также дают прекрасные результаты.
В дальнейшем изложении предполагается, что читатель знаком с содержанием лекции 25, где были определены основные понятия и термины,используемые в генетических алгоритмах, а также описан простой генетический алгоритм (ПГА).
Кратко напомним необходимые нам сведения о ПГА, содержащем следующие этапы:
- Формирование начальной популяции;
- Подбор особей в родительские пары;
- Получение дочерних особей с помощью оператора репродукции (скрещивания);
- Выполнение оператора мутации;
- Отбор особей для формирования следующего поколения;
- Проверка условий окончания процесса эволюции.
На первом этапе создаются особи начальной популяции. Создание начальной популяции осуществляется, как правило, произвольным образом, в большинстве случаев особи формируются из случайных данных. Это позволяет осуществить разброс по пространству поиска, т. е. в данном случае этап создания начальной популяции подобен методу случайного поиска.
На втором этапе отбора для каждой особи определяется ее приспособленность, оцениваемая с помощью фитнес-функции. Напомним, что фитнес-функция есть мера качества решения. Затем с помощью оператора селекции осуществляется отбор. Отбор кандидатов (особей) для участия в процессе репродукции производится по принципу: чем выше приспособленность особи, тем выше вероятность ее участия в процессе скрещивания. Этап отбора представляет собой аналог дарвиновского выживания сильнейших применительно к особям.
