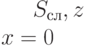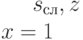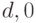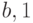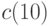|
Добрый день можно поинтересоваться где брать литературу предложенную в курсе ?Большинство книг я не могу найти в известных источниках |
Построение тестов для устройств с памятью на основе экспериментов с автоматами
Одной из самых сложных проблем при создании систем автоматизированного проектирования и диагностики дискретных устройств является задача разработки алгоритмов моделирования и генерации проверяющих тестов цифровых устройств с памятью. Это объясняется дополнительными трудностями, возникающими из-за неопределенности начального состояния ЦУ с памятью и возможных состязаний сигналов. В силу этих обстоятельств методы построения проверяющих тестов и моделирования неисправных ЦУ с памятью разработаны не так хорошо, как для комбинационных ЦУ. Следует отметить, что применение методов контролепригодного проектирования, позволяющее свести диагностику ЦУ с памятью к диагностике комбинационных ЦУ не всегда возможно и эффективно [22.1-22.3]. Поэтому в настоящий момент данная задача является по-прежнему актуальной.
Существующие подходы к тестированию устройств с памятью можно классифицировать на три группы. К первой можно отнести методы, основанные на теории экспериментов с конечными автоматами (КА), которые являются классической моделью ЦУ с памятью. Методы данной группы позволяют проверить неисправность, приводящую к любому изменению таблицы переходов/выходов, задающую КА исправного устройства. Существенным достоинством автоматного подхода является высокая степень полноты контроля неисправностей и широкий класс возможных неисправностей. К недостаткам относят очень высокую сложность построения и длину тестовой последовательности, а также в ряде случаев необходимость построения автоматной модели на основе структурного описания ЦУ. Необходимость построения (в ряде случаев) автоматной модели для исходного структурного описания ЦУ,
экспоненциальный рост сложности табличного представления автомата 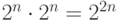 (
( - количество элементарных ячеек памяти -
триггеров или линий обратных связей,
- количество элементарных ячеек памяти -
триггеров или линий обратных связей,  - количество состояний автомата рис. 7.1, 7.2) и большая длина получаемых тестов относятся к недостаткам автоматных методов с практической точки зрения построения проверяющих тестов для интегральных схем.
- количество состояний автомата рис. 7.1, 7.2) и большая длина получаемых тестов относятся к недостаткам автоматных методов с практической точки зрения построения проверяющих тестов для интегральных схем.
Вторую группу составляют структурные методы генерации проверяющих тестов, использующих в качестве модели ЦУ последовательностную логическую схему, или его укрупненное структурное описание. ЦУ на логическом уровне, как правило, описываются разработчиками в виде логической схемы, поэтому необходимость в каких-либо дополнительных построениях отсутствует. Как показано ранее (
"Модели цифровых устройств"
), ЦУ без памяти представляются комбинационными логическими схемами, ЦУ с памятью - последовательностными логическими схемами [22.1-22.4].
В большинстве структурных методов для ЦУ с памятью процесс построения проверяющего теста заключается в получении входной последовательности, различающей исправное и неисправное ЦУ, с помощью применения разнообразных многозначных моделей и алгоритмов активизации критических путей, а также некоторых других подходов [22.1,22.2]. В этом случае сложность построения тестов для ЦУ с памятью определяется числом линий обратных связей  , значения сигналов на которых определяет текущее состояние ЦУ с памятью. Напомним, что состояние конечного автомата соответствует и определяется вектором значений сигналов линий обратных связей или иначе переменных состояния ЦУ с памятью. Как, уже говорилось ранее, в случае автоматного подхода сложность построения теста определяется числом состояний конечного автомата, которое может достигать числа
, значения сигналов на которых определяет текущее состояние ЦУ с памятью. Напомним, что состояние конечного автомата соответствует и определяется вектором значений сигналов линий обратных связей или иначе переменных состояния ЦУ с памятью. Как, уже говорилось ранее, в случае автоматного подхода сложность построения теста определяется числом состояний конечного автомата, которое может достигать числа  .
Очевидно, что даже при небольшом числе линий обратных связей сложность построения теста автоматными методами может быть высокой. Существует так называемая проблема "взрыва состояний" - начиная с некоторого значения
.
Очевидно, что даже при небольшом числе линий обратных связей сложность построения теста автоматными методами может быть высокой. Существует так называемая проблема "взрыва состояний" - начиная с некоторого значения  , число состояний КА резко возрастает (происходит "взрыв" их количества). С другой стороны использование структурной модели последовательностных логических схем и многозначных моделей обеспечивает относительно невысокую по числу переменных состояния сложность структурных алгоритмов. Однако в силу некоторых особенностей структурных методов, о которых пойдет речь ниже, получаемые тесты обладают недостаточно высокой полнотой по сравнению с автоматными методами.
, число состояний КА резко возрастает (происходит "взрыв" их количества). С другой стороны использование структурной модели последовательностных логических схем и многозначных моделей обеспечивает относительно невысокую по числу переменных состояния сложность структурных алгоритмов. Однако в силу некоторых особенностей структурных методов, о которых пойдет речь ниже, получаемые тесты обладают недостаточно высокой полнотой по сравнению с автоматными методами.
Поэтому кроме классических автоматного и структурного подхода, рассматриваются комбинированные или функциональные методы построения тестов для ЦУ с памятью, составляющие третью группу методов. В данной группе методов осуществляется попытка реализовать для структурного представления ЦУ с памятью преимуществ автоматных методов, сохраняя при этом относительно невысокую по числу переменных состояния сложность структурных алгоритмов.
22.1 Основы экспериментов с конечными автоматами
В случае автоматного подхода решение задачи поиска теста сводится к решению проблемы распознавания заданного КА в классе неисправных КА [22.5]. При этом неисправное устройство моделируется КА, отличным от данного.
Определение 22.1 Конечный неинициальный автомат задается совокупностью пяти объектов 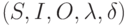 , где
, где
 - множество состояний ДУ с памятью,
- множество состояний ДУ с памятью,
 - входной алфавит,
- входной алфавит,
 - выходной алфавит,
- выходной алфавит,
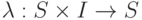 - функция перехода,
- функция перехода,
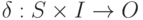 - функция выхода.
- функция выхода.
Последовательностная логическая схема, реализующая заданные в табл. 22.1,табл. 22.2 соответственно исправный и неисправный (наличие константной неисправности const 0 на линии  ) автоматы.
) автоматы.
Классическими представителями автоматного подхода построения идентифицирующих и проверяющих тестовых последовательностей являются методы, основанные на построении дерева преемников состояний (ДПС+) и дерева предшественников состояний (ДПС-)
[22.5] расщепляемого автомата  , содержащего автоматы
, содержащего автоматы  и
и 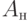 , соответствующие исправному и неисправному устройствам.
Функционирование
, соответствующие исправному и неисправному устройствам.
Функционирование  и
и 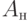 описывается таблицами переходов и выходов. Например, в табл. 22.1 и табл. 22.2 приведены автоматы
описывается таблицами переходов и выходов. Например, в табл. 22.1 и табл. 22.2 приведены автоматы  и
и 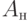 , структурно реализуемые последовательностной логической схемой (рис. 22.1), исправной и содержащей неисправность
, структурно реализуемые последовательностной логической схемой (рис. 22.1), исправной и содержащей неисправность 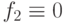 соответственно.
соответственно.
Приведем основные понятия, связанные с конструкциями ДПС+ и ДПС-. При их описании воспользуемся терминологией, принятой в [22.5]. Нулевой уровень как ДПС+, так и ДПС- содержит единственную вершину, связанную с  -группой, которая состоит из одного
-группой, которая состоит из одного 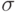 -множества, содержащего все состояния
-множества, содержащего все состояния  и
и 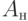 . Для автоматов, описанных в табл. 22.1 и табл. 22.2 - это
. Для автоматов, описанных в табл. 22.1 и табл. 22.2 - это 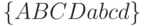 . Каждая вершина
. Каждая вершина  -го (
-го ( ) уровня расщепляется на
) уровня расщепляется на  вершин, соответствующих всем символам входного алфавита, где
вершин, соответствующих всем символам входного алфавита, где  - мощность входного алфавита. В нашем случае вершина расщепляется на 2 вершины, соответствующие
- мощность входного алфавита. В нашем случае вершина расщепляется на 2 вершины, соответствующие 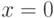 и
и 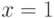 .
При этом
.
При этом  -группа
-группа 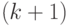 -го уровня содержит состояния, являющиеся преемниками состояний по соответствующему входному сигналу
-го уровня содержит состояния, являющиеся преемниками состояний по соответствующему входному сигналу  -группы
-группы  -го уровня в случае ДПС+ и предшественниками состояний
-го уровня в случае ДПС+ и предшественниками состояний  -группы
-группы  -го уровня в случае ДПС-.
-го уровня в случае ДПС-. 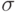 -множества
-множества  -группы
-группы 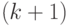 -го уровня получаются путем разбиения на подмножества состояний преемников (ДПС+) или предшественников (ДПС-)
-го уровня получаются путем разбиения на подмножества состояний преемников (ДПС+) или предшественников (ДПС-) 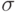 -множества
-множества  -го уровня таким образом, что два состояния включаются в одно и то же
-го уровня таким образом, что два состояния включаются в одно и то же 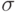 -множество, если и только если они вырабатывают одинаковую реакцию на соответствующий входной сигнал.
-множество, если и только если они вырабатывают одинаковую реакцию на соответствующий входной сигнал.
Определение 22.2 Назовем  -группу гомогенной, если в ней состояния исправного и неисправного автоматов
-группу гомогенной, если в ней состояния исправного и неисправного автоматов  и
и 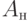 находятся отдельно в разных
находятся отдельно в разных 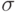 -множествах.
-множествах.
ДПС является бесконечной структурой, поэтому обычно рассматриваются его усеченные варианты. Введем понятия прямого различающего дерева (ПРД) и обратного различающего дерева (ОРД).
Определение 22.3 ПРД - это дерево преемников состояний, в котором вершина 
 -го уровня становится оконечной при выполнении одного из следующих условий:
-го уровня становится оконечной при выполнении одного из следующих условий:
- для
 -группы
-группы 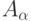 , связанной с вершиной
, связанной с вершиной  , существует
, существует  -группа
-группа 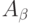 , связанная с некоторой вершиной
, связанная с некоторой вершиной 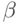 уровня, предшествующего
уровня, предшествующего  -му, такая, что для каждого
-му, такая, что для каждого  -множества из
-множества из 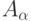 существует включающее его
существует включающее его  -множество из
-множество из 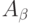 ;
;
- существует вершина
 -го уровня (возможно сама
-го уровня (возможно сама  ), связанная с гомогенной
), связанная с гомогенной  -группой.
-группой.
На рис. 22.2 представлен фрагмент ПРД для автомата 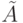 , содержащего
, содержащего 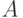 и
и 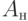 , описанных в таблицах 22.1, 22.2. Все вершины 4-го уровня этого дерева являются оконечными, так как
, описанных в таблицах 22.1, 22.2. Все вершины 4-го уровня этого дерева являются оконечными, так как  -группа
-группа 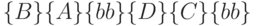 является гомогенной. Путь, связывающий вершину нулевого уровня ПРД с вершиной, привязанной к гомогенной
является гомогенной. Путь, связывающий вершину нулевого уровня ПРД с вершиной, привязанной к гомогенной  -группе, определяет тест данной неисправности. В нашем примере путь, связывающий вершину нулевого уровня ПРД с вершиной, привязанной к гомогенной
-группе, определяет тест данной неисправности. В нашем примере путь, связывающий вершину нулевого уровня ПРД с вершиной, привязанной к гомогенной  -группе
-группе 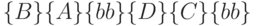 (на рис. 22.2 выделен жирной линией), позволяет определить,
что тестом неисправности
(на рис. 22.2 выделен жирной линией), позволяет определить,
что тестом неисправности  (рис. 22.1) является входная последовательность
(рис. 22.1) является входная последовательность 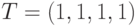 .
.
Определение 22.4 Обратное различающее дерево (ОРД) - это дерево предшественников состояний, в котором вершина 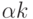 -го уровня становится оконечной при выполнении условия 1) или условия 2) из определения 7.3.
-го уровня становится оконечной при выполнении условия 1) или условия 2) из определения 7.3.
Путем построения ОРД также могут быть найдены тестовые последовательности. На рис. 22.3 представлен фрагмент ОРД для автомата 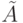 , содержащего
, содержащего  и
и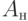 , описанные в табл. 22.1, 22.2. Также как и в ПРД, все ветви 4-го уровня этого дерева являются оконечными, так как
, описанные в табл. 22.1, 22.2. Также как и в ПРД, все ветви 4-го уровня этого дерева являются оконечными, так как  -группа
-группа  , связанная с одной из вершин 4-го уровня, является гомогенной. Путь между вершиной ОРД, связанной с гомогенной
, связанная с одной из вершин 4-го уровня, является гомогенной. Путь между вершиной ОРД, связанной с гомогенной  -группой, и вершиной нулевого уровня определяет тест данной неисправности.
В нашем примере путь между вершиной ОРД, связанной с гомогенной
-группой, и вершиной нулевого уровня определяет тест данной неисправности.
В нашем примере путь между вершиной ОРД, связанной с гомогенной  -группой
-группой  , и вершиной нулевого уровня (рис. 22.3, выделен жирной линией), позволяет определить, что как это было получено и для ПРД, тестом данной неисправности
, и вершиной нулевого уровня (рис. 22.3, выделен жирной линией), позволяет определить, что как это было получено и для ПРД, тестом данной неисправности  (рис. 22.1) является входная последовательность
(рис. 22.1) является входная последовательность 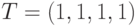 .
.