|
Добрый день можно поинтересоваться где брать литературу предложенную в курсе ?Большинство книг я не могу найти в известных источниках |
Московский государственный университет путей сообщения
Опубликован: 06.09.2012 | Доступ: свободный | Студентов: 1253 / 182 | Оценка: 5.00 / 5.00 | Длительность: 35:22:00
Темы: САПР, Аппаратное обеспечение
Специальности: Разработчик аппаратуры
Теги:
Лекция 25:
Эволюционные методы генерации тестов
Аннотация: В лекции изложен генетический алгоритм (ГА) и его применение для построения проверяющих тестов цифровых схем. Определены основные понятия простого ГА. Описано использование ГА в генерации тестов комбинационных схем. Рассмотрен ГА для генерации тестов последовательностных схем, проблемно-ориентированные генетические операторы кроссинговера и мутации. Представлены основные виды фитнесс-функций, используемых при построении тестов. Рассмотрены вопросы реализации ГА построения тестов.
Ключевые слова: САПР, самоорганизация, генетический алгоритм, эволюционное программирование, мутация, хромосомы, копирование, вероятность, ПО, поиск, указатель, эволюция, множества, fitness, функция, значение, логическое моделирование, входной, операторы, инвертирование, очередь, тестовый набор, операции, информация, мера, мощность, затраты, вектор, детерминированный метод, размерность, коэффициенты, длина, параметр, программа, алгоритм, вычисление, моделирование, переменная, бит, активность, потомок, определение, улучшение, псевдокод
Для повышения уровня "интеллекта" и эффективности современных САПР компьютерных систем, расширения их возможностей применяются различные методы искусственного интеллекта. Одним из самых перспективных направлений является использование эволюционных вычислений.
Особенности идей теории эволюции и самоорганизации заключаются в том, что они находят свое подтверждение не только для биологических систем, успешно развивающихся многие миллиарды лет. В настоящее время бурно развивается новое направление в теории и практике искусственного интеллекта эволюционные вычисления - термин, обычно используемый для общего описания алгоритмов поиска, оптимизации или обучения, основанных на некоторых формализованных принципах естественного эволюционного отбора. Эволюционные вычисления используют различные модели эволюционного процесса. Среди них можно выделить следующие основные парадигмы:
- генетические алгоритмы;
- эволюционные стратегии;
- эволюционное программирование;
- генетическое программирование.
Отличаются они, в основном, способом представления искомых решений и различным набором используемых в процессе моделирования эволюции операторов. Отметим, что в настоящее время все парадигмы используются при генерации тестов цифровых систем.
25.1 Простой генетический алгоритм
Генетические алгоритмы (ГА) [25.1], являясь одной из парадигм эволюционных вычислений, представляют собой алгоритмы поиска, построенные на принципах, сходных с принципами естественного отбора.
В соответствии с ними простой ГА использует три основных оператора: репродукция, кроссинговер, мутация. При репродукции хромосомы копируются согласно их значениям ЦФ. Копирование лучших хромосом с большими значениями ЦФ определяет большую вероятность их попадания в следующую генерацию. Оператор репродукции реализует принцип "выживания сильнейших" по Дарвину.
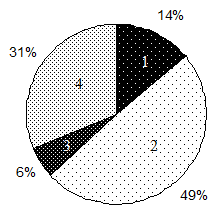
Самый простой (и популярный) метод реализации ОР - построение асимметричного колеса рулетки, в которой каждая хромосома имеет сектор, пропорциональный ее значению ЦФ. Например, "колесо рулетки" имеет следующий вид, представленный на рис. 25.1.
Для селекции хромосом используется случайный поиск на основе колеса рулетки. При этом колесо рулетки вращается и после останова ее указатель определяет хромосому для селекции в промежуточную популяцию. Очевидно, что хромосома, которой соответствует больший сектор рулетки, имеет большую вероятность попасть в следующее поколение. В результате выполнения оператора репродукции из текущей популяции формируется промежуточная популяция, хромосомы которой будут использованы для построения поколения с помощью операторов (кроссинговера) скрещивания и мутации.
Оператор кроссинговера (ОК) обычно выполняется в три этапа:
- Два стринга (хромосомы, особи)
и
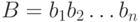выбираются случайно из промежуточной популяции после репродукции;
- Выбирается также случайно точка кроссинговера
;
-
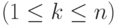Хромосомы
и 
обмениваются частями после -й позиции и производят два новых стринга
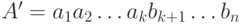и
.
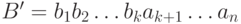Например, для родительских особей
,
При точке кроссинговера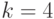 
получаем следующие особи - потомки
.
Следует отметить, что для отобранных родительских особей оператор кроссинговера выполняется с некоторой заданной вероятностью
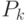(обычно 
). То есть отобранные родители не всегда дают потомство.
Оператор мутации (ОМ) случайным образом (с небольшой вероятностью 
) изменяет произвольный ген (элемент) стринга.
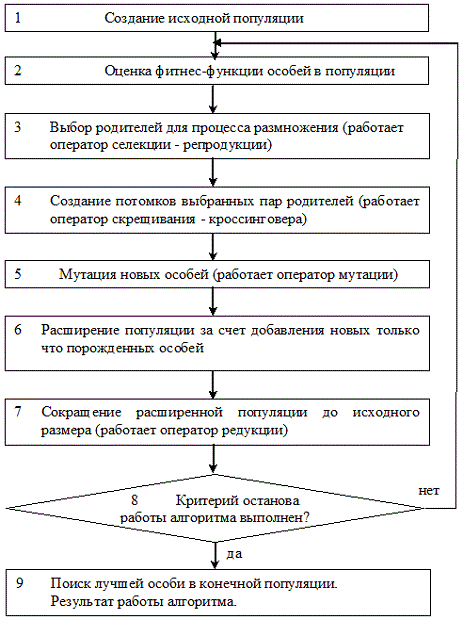
Используя эти три основные оператора, популяция (множество потенциальных решений данной проблемы) эволюционирует от поколения к поколению. Эволюция такой искусственной популяции представлена на рис. 25.2.
Таким образом, чтобы задать генетический алгоритм, необходимо определить понятия особи, популяции, операторов скрещивания и мутации, задать оценочную функцию. Очевидно также, что эффективность генетического алгоритма зависит от целого ряда параметров: размера популяции, метода выбора особей из предыдущей популяции, скрещивания и мутации, вероятностей выполнения операторов кроссинговера и мутации, а также вида оценочной функции.
Дмитрий Медведевских