|
Добрый день можно поинтересоваться где брать литературу предложенную в курсе ?Большинство книг я не могу найти в известных источниках |
Жадные алгоритмы поиска масок
Алгоритмы поиска маски ориентированы на решение задач сокращения ДИ. Вместе с тем эти алгоритмы могут быть использованы и для решения других задач. В качестве примера приведем задачи классификации объектов, часто встречающиеся в практических приложениях. В подобного рода задачах каждый объект из заданного множества характеризуется некоторой совокупностью признаков, имеющих конкретные числовые (и/или иного типа) значения. Поскольку упомянутая совокупность признаков может иметь большую мощность, то для идентификации предъявленного объекта, характеризуемого конкретным набором значений признаков, потребуется хранить большой объем информации. В этой ситуации проблема сокращения исходной информации эквивалентна проблеме сокращения диагностической информации. Проводя аналогию между задачей классификации объектов по совокупности значений их признаков и задачей сокращения диагностической информации, можно сказать, что упомянутая совокупность признаков в первой задаче идентична ТФН для конкретной неисправности во второй, а полная информация об объектах 1-ой задачи идентична полной ТФН во 2-ой задаче.
Проводя дальнейшую аналогию между задачами классификации и сокращения ДИ с помощью масок обратимся к алгоритмам решения задач классификации с целью их применения к задачам поиска маски, предложенным в [2].
Одним из популярных подходов к решению проблемы сокращения исходной информации является использование механизма деревьев решений.
Деревья решений представляют собой иерархическую структуру классифицирующих правил типа "если ... то ...", имеющую вид дерева. Для того чтобы решить, к какому классу отнести некоторый объект, требуется ответить на вопросы, стоящие в узлах этого дерева, начиная от его корня. Формулировка такого вопроса обычно заключается в проверке значения некоторого атрибута предъявленного объекта. Дуги, исходящие из узла дерева к его потомкам, помечаются вариантами ответов на вопрос, заданный в данном узле. Каждый лист такого дерева соответствует классу со значениями атрибутов, приписанными дугам пути от корня до этого листа.
Таким образом, имея построенное дерево решений, отпадает необходимость в хранении всей совокупности признаков: можно хранить информацию только о тех атрибутах, которые упоминаются в узлах дерева решений.
Для построении деревьев решений часто используется алгоритм C4.5, предложенный в [1]. Напомним основные моменты этого алгоритма.
Пусть задано множество объектов обучающей выборки , где каждый объект описывается множеством атрибутов  . Пусть объекты обучающей выборки являются элементами классов из множества
. Пусть объекты обучающей выборки являются элементами классов из множества  .
.
Построение дерева происходит сверху вниз. Сначала создается корень дерева, затем потомки корня и т. д. Каждому узлу дерева ставится в соответствие некоторое подмножество множества  . Корню дерева ставится в соответствие само множество
. Корню дерева ставится в соответствие само множество  .
.
Процесс построения дерева заключается в следующем. Первоначально построим дерево, состоящее только из корня. Следующие шаги необходимо выполнить для каждого листа уже построенного дерева, которому соответствует множество объектов более чем одного класса.
Пусть данному узлу дерева соответствует множество объектов P' P классов из 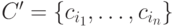 , а
, а 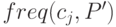 - количество элементов из множества
- количество элементов из множества 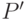 , принадлежащих классу
, принадлежащих классу 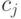 . Тогда величина
. Тогда величина
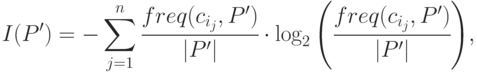 |
( 31.1) |
где  - количество элементов в множестве
- количество элементов в множестве 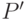 , дает оценку среднего количества информации, необходимой для идентификации объекта из множества
, дает оценку среднего количества информации, необходимой для идентификации объекта из множества 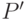 .
.
Если произвести разбиение множества 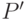 в зависимости от значений атрибута
в зависимости от значений атрибута  на
на 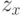 подмножеств, то ту же оценку, но уже после разбиения, дает выражение
подмножеств, то ту же оценку, но уже после разбиения, дает выражение
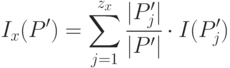 |
( 31.2) |
В принятых обозначениях алгоритм C4.5 состоит из следующих шагов:
- Необходимо выбрать такой атрибут
 , который доставляет максимум величине
, который доставляет максимум величине
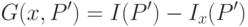
( 31.3) - Для данного узла дерева создать
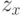 потомков.
потомков.
- Каждому потомку данного узла поставить в соответствие подмножество объектов из множества
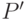 , имеющих одно и то же значение атрибута
, имеющих одно и то же значение атрибута  , а дугу от узла к потомку пометить соответствующим значением.
, а дугу от узла к потомку пометить соответствующим значением.
Процесс построения дерева заканчивается, когда всем листьям дерева будут соответствовать множества объектов одного класса.
Для задачи сокращения ДИ признаки, проверяемые в узлах дерева решений, могут быть взяты в качестве элементов маски ДИ.
С учетом обозначений, введенных ранее, множество технических состояний  выступает в роли множества
выступает в роли множества  для алгоритма C4.5. Это же самое множество
для алгоритма C4.5. Это же самое множество  представляет набор классов
представляет набор классов  , т. е. в нашем случае каждый класс представлен лишь одним объектом в обучающей выборке.
СПР представляет исходные данные для построения дерева решений: каждая точка проверки ДУ выполняет роль атрибута объектов, а каждая строка СПР описывает значения этих атрибутов.
, т. е. в нашем случае каждый класс представлен лишь одним объектом в обучающей выборке.
СПР представляет исходные данные для построения дерева решений: каждая точка проверки ДУ выполняет роль атрибута объектов, а каждая строка СПР описывает значения этих атрибутов.
Поскольку каждый класс представлен лишь одним объектом в обучающей выборке, то формула (31.1) примет следующий вид:
 |
( 31.4) |
В связи с тем, что возможных значений атрибутов всего два (0 или 1), получаемое дерево решений является бинарным, где в каждом конкретном узле множество 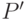 разделяется на два подмножества
разделяется на два подмножества 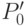 и
и 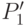 в соответствии со значениями атрибута , доставляющего максимум величине
в соответствии со значениями атрибута , доставляющего максимум величине
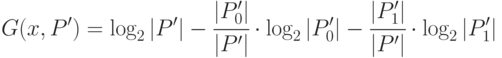 |
( 31.5) |
Формула (31.5) получена из (31.3) с учетом (31.4). Очевидно, что 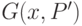 в (31.5) будет иметь максимум в том случае, если множество
в (31.5) будет иметь максимум в том случае, если множество 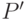 делится по значениям атрибута
делится по значениям атрибута  на два подмножества с равным числом элементов.
на два подмножества с равным числом элементов.
Так как количество листьев в результирующем дереве равно 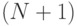 , а само дерево является бинарным, можно сделать вывод, что количество внутренних узлов дерева, т. е. узлов, в которых производится проверка значений атрибутов, не превышает величины
, а само дерево является бинарным, можно сделать вывод, что количество внутренних узлов дерева, т. е. узлов, в которых производится проверка значений атрибутов, не превышает величины  .
При наилучшем исходе алгоритм C4.5 строит идеально сбалансированное дерево, в котором на любом пути от корня до листа проверяются значения одного и того же набора атрибутов, в котором
.
При наилучшем исходе алгоритм C4.5 строит идеально сбалансированное дерево, в котором на любом пути от корня до листа проверяются значения одного и того же набора атрибутов, в котором 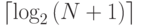 элементов. Эти крайние значения как раз и соответствуют объему оптимальной маски. Таким образом, с помощью алгоритма C4.5 можно получить маску, по объему близкую к оптимальной.
элементов. Эти крайние значения как раз и соответствуют объему оптимальной маски. Таким образом, с помощью алгоритма C4.5 можно получить маску, по объему близкую к оптимальной.
Алгоритм C4.5 ориентирован на построение дерева решений наиболее приближенного к идеально сбалансированному, т. е. на сокращение среднего числа атрибутов, необходимого для идентификации предъявленного объекта. Таким образом, для каждого класса выбирается индивидуальная совокупность атрибутов, необходимая для идентификации его объектов. По сути, построение дерева решений ориентировано на построение алгоритма классификации объекта с минимальным числом шагов и при этом не преследуется цели сокращения используемой информации, необходимой для такого алгоритма. Но в случае сокращения ДИ алгоритм получения реакции на диагностический тест уже известен, а для большего сокращения информации целесообразно найти некое единое множество атрибутов, по которому можно было бы идентифицировать любой объект. Естественно, объединение упомянутых индивидуальных совокупностей для всех классов может иметь существенно большую мощность, чем такое единое множество.
Следующий алгоритм [3], базирующийся на идеях алгоритма C4.5, направлен на нахождение упомянутого единого множества атрибутов.
Отличие предлагаемого алгоритма от алгоритма C4.5 состоит в том, что построение дерева производится по уровням, с выбором одного атрибута для проверки во всех узлах уровня. На начальном уровне присутствует только один узел - корень дерева. На каждом последующем шаге рассматривается очередной уровень дерева и генерируется уровень его потомков. Для получения нового уровня выбирается атрибут , который доставляет максимум величине
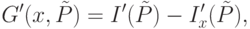 |
( 31.6) |
где 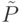 - совокупность множеств объектов, соответствующих узлам текущего уровня, а величины
- совокупность множеств объектов, соответствующих узлам текущего уровня, а величины 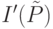 и
и 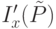 равны соответственно
равны соответственно
 |
( 31.7) |
и
 |
( 31.8) |
Так же как и в алгоритме C4.5, процесс построения дерева заканчивается, если на очередном уровне каждому узлу дерева будет соответствовать множество объектов одного класса.
Содержательный смысл такого построения состоит в следующем: на каждом уровне дерева выбирается атрибут, проверка которого максимально уменьшает среднее количество информации, необходимой для идентификации любого объекта из множества  .
.
Переформулируем последний алгоритм применительно к задаче поиска маски. В этом случае стоит учесть, что роль атрибутов выполняют точки проверки ЦУ. Также обратим внимание на то, что после вычисления множеств, соответствующих вершинам очередного уровня дерева, необходимость в хранении информации о предшествующих уровнях отпадает.
Совокупность множеств, соответствующих вершинам очередного уровня дерева, представляет разбиение исходного множества классов - в нашем случае множества  . Т. е. в ходе очередной итерации алгоритма достаточно по разбиению множества
. Т. е. в ходе очередной итерации алгоритма достаточно по разбиению множества  , соответствующего предыдущему уровню дерева, построить разбиение, соответствующее очередному уровню.
, соответствующего предыдущему уровню дерева, построить разбиение, соответствующее очередному уровню.
Разбиение множества технических состояний  производится в соответствии со значениями в точках проверки. Каждая точка проверки разбивает множество технических состояний
производится в соответствии со значениями в точках проверки. Каждая точка проверки разбивает множество технических состояний  на два блока (подмножества) следующим образом: технические состояния, для которых значение в данной точке проверки равно единице, помещаются в первый блок, а неисправности, для которых значение равно нулю - во второй.
Можно производить дальнейшее разбиение каждого из полученных блоков в соответствии со значениями в других точках проверки. Если СПР обладает свойством различения всех технических состояний, то, производя последовательно разбиение множества
на два блока (подмножества) следующим образом: технические состояния, для которых значение в данной точке проверки равно единице, помещаются в первый блок, а неисправности, для которых значение равно нулю - во второй.
Можно производить дальнейшее разбиение каждого из полученных блоков в соответствии со значениями в других точках проверки. Если СПР обладает свойством различения всех технических состояний, то, производя последовательно разбиение множества  с помощью всех точек проверки, получим в результате одноэлементные блоки.
с помощью всех точек проверки, получим в результате одноэлементные блоки.
В целях решения задачи оптимизации маски можно ввести ограничение объема полученной маски. Такое ограничение будет заключаться в установке предельного значения количества уровней дерева, или, другими словами, определении числа итераций алгоритма.
Итак, исходя из изложенного, сформулируем формальное описание алгоритма.
Алгоритм 1 ( Жадный алгоритм поиска единой маски ДИ ).
Вход: Словарь полной реакции;  - множество технических состояний;
- множество технических состояний;  - максимальный объем маски результата (по умолчанию
- максимальный объем маски результата (по умолчанию  ).
).
- Положить
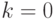 ,
,
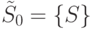 ,
,
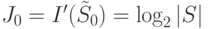 .
. - Положить
 .
. - Найти точку проверки
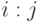 , доставляющую максимум величине
, доставляющую максимум величине
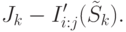
( 31.9) - Положить
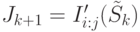 .
. - Если
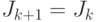 , выдать
, выдать  и закончить алгоритм. В противном случае перейти к шагу 6.
и закончить алгоритм. В противном случае перейти к шагу 6. - Произвести разбиение блоков из
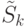 в соответствии со значениями точки проверки
в соответствии со значениями точки проверки 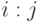 в СПР. Результат разбиения записать в
в СПР. Результат разбиения записать в  .
. - Включить точку проверки
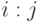 в маску
в маску  , положить
, положить 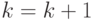 .
. - Если
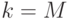 , то выдать
, то выдать  и закончить алгоритм. Иначе перейти к шагу 3.
и закончить алгоритм. Иначе перейти к шагу 3.
Замечение 1. Ограничение объема возвращаемой маски в алгоритме 1 по умолчанию числом 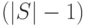 носит условный характер, так как при отказе от этого ограничения объем любой маски, полученной с помощью этого алгоритма, не превысит величины
носит условный характер, так как при отказе от этого ограничения объем любой маски, полученной с помощью этого алгоритма, не превысит величины 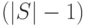 .
.
Действительно, при добавлении в алгоритме очередной точки проверки в маску  происходит дополнительное разбиение блоков в
происходит дополнительное разбиение блоков в 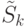 . Из того, что
. Из того, что 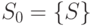 следует, что провести разбиение блока из
следует, что провести разбиение блока из  на одноэлементные блоки можно максимум за
на одноэлементные блоки можно максимум за  итераций.
итераций.
Рассмотрим работу полученного алгоритма на примере схемы C17 (рис. 27.1). Найдем единую маску для СПР, представленного в табл. 27.5. После первых двух шагов алгоритма имеем:
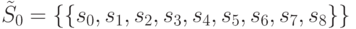 ,
,
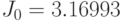 ,
,
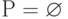 . На третьем шаге алгоритма получаем следующие результаты:
. На третьем шаге алгоритма получаем следующие результаты:
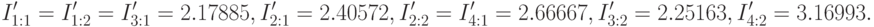
Следовательно величина (6.9) достигает своего максимума при использовании точек проверки 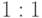 ,
,  и
и 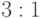 . Выполним шаги Ошибка! Источник ссылки не найден.-Ошибка! Источник ссылки не найден. алгоритма, предполагая, что на третьем шаге выбрана точка проверки
. Выполним шаги Ошибка! Источник ссылки не найден.-Ошибка! Источник ссылки не найден. алгоритма, предполагая, что на третьем шаге выбрана точка проверки 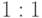 . После первой итерации алгоритма получим
. После первой итерации алгоритма получим
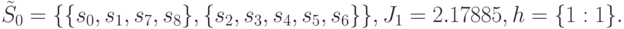
На третьем шаге следующей итерации алгоритма получаем:
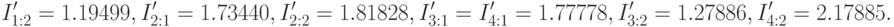
что означает однозначный выбор точки проверки  . Ситуация после окончания второй итерации становится следующей:
. Ситуация после окончания второй итерации становится следующей:
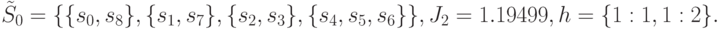
На очередном проходе алгоритма вычисления дают следующие результаты.
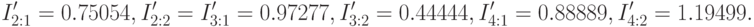
откуда получаем
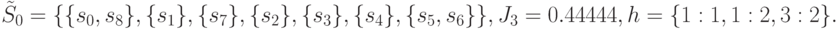
Как видим, после трех итераций алгоритма остались неразличимыми две пары технических состояний  и
и 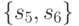 . Следующая итерация приводит к величинам
. Следующая итерация приводит к величинам

означающим, что любая из точек проверок
 ,
, ,
, различает одну из этих пар состояний. Выбор точки проверки
различает одну из этих пар состояний. Выбор точки проверки  приведет к значениям
приведет к значениям
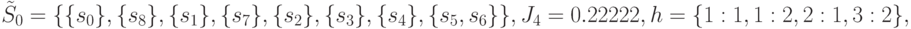
после чего на пятой итерации получим
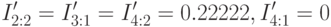
и включая в маску получим

На шестой итерации алгоритма получаем значения 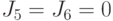 , после чего алгоритм завершает свою работу. Результат работы алгоритма - маска
, после чего алгоритм завершает свою работу. Результат работы алгоритма - маска 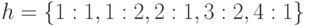 .
.
