|
Добрый день можно поинтересоваться где брать литературу предложенную в курсе ?Большинство книг я не могу найти в известных источниках |
Модели цифровых устройств
Данный раздел содержит различные формы представления моделей, которые используются при моделировании и тестировании ЦУ. Прежде всего, мы рассмотрим вопросы моделирования на уровне логических элементов или логическом моделировании ЦУ. При этом, как правило, элементы, составляющие ЦУ, описываются с помощью логических уравнений (булевых функций), которые отражают логику их функционирования. Кроме этого исследуются функциональные модели ЦУ на уровне регистровых передач.
Объектом наших исследований являются ДУ, которые делятся на два класса [ 2.2 ] , [ 2.5 ] : комбинационные и последовательностные устройства. ЦУ называется комбинационным, или ЦУ без памяти, если значения его выходных сигналов однозначно определяются только значениями входных сигналов. Последовательностным, или ЦУ с памятью, называется устройство, у которого значения выходных сигналов в данный момент времени зависят от значений входных сигналов в текущий момент и от внутреннего состояния объекта в предыдущий момент времени, определяемого значениями сигналов на линиях обратных связей. При построении моделей ЦУ мы рассмотрим три подхода: функциональный, структурный и представление ДУ языками описания аппаратуры (hardware design languages - HDL).
Функциональные модели
Суть функционального подхода заключается в абстрагировании от внутренней организации устройства и рассмотрении только его логики функционирования. Как правило, под ЦУ подразумеваются устройства, перерабатывающие двоичную информацию.
Модели комбинационных схем
В качестве функциональной модели комбинационных устройств, чаще всего, используют систему булевых функций:
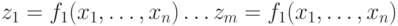
где 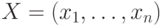 - входные,
- входные, 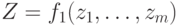 - выходные переменные, принимающие двоичные значения
- выходные переменные, принимающие двоичные значения 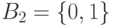 . Данная система булевых функций описывает комбинационное ДУ, которое имеет
. Данная система булевых функций описывает комбинационное ДУ, которое имеет  входов,
входов,  выходов и представлено на рис. 2.1 .
выходов и представлено на рис. 2.1 .
Здесь каждая булева функция  - отображение
- отображение  . Простейшим способом представления булевой функции является таблица истинности. Например, в табл.2.1 приведена таблица истинности для булевой функции трех переменных.
. Простейшим способом представления булевой функции является таблица истинности. Например, в табл.2.1 приведена таблица истинности для булевой функции трех переменных.
Кроме этих таблиц часто используются также табличные модели в виде так называемых "примитивных" (простых) кубов. Эти кубы в сжатом виде фактически представляют ту же самую информацию. Один "примитивный" куб объединяет несколько "соседних" строк таблицы истинности, на которых булева функция принимает одно и тоже значение. Под "соседними" здесь понимаются строки, отличающиеся значением одного (или более) бита. В отличие от таблиц истинности такие кубы используют не двоичный алфавит 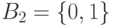 , а троичный алфавит
, а троичный алфавит 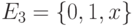 , где символ
, где символ  представляет неопределенное значение (
представляет неопределенное значение ( или
или  ) переменной. В табл.2.2 представлена табличная модель в виде "примитивных" кубов той же булевой функции (
таблица
2.1).
) переменной. В табл.2.2 представлена табличная модель в виде "примитивных" кубов той же булевой функции (
таблица
2.1).
В табл. 2.2 первая строка ("примитивный" куб – 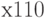 ) объединяет третью (
) объединяет третью (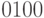 ) и седьмую (
) и седьмую (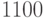 ) строки исходной таблицы истинности. Отметим, что третья стока (куб
) строки исходной таблицы истинности. Отметим, что третья стока (куб  ) объединяет четыре строки таблицы истинности, имеющих всевозможные значения переменных
) объединяет четыре строки таблицы истинности, имеющих всевозможные значения переменных  и
и  и одно и тоже значение булевой функции
и одно и тоже значение булевой функции  . Фактически, "примитивный" куб соответствует простой импликанте
[
2.6
]
.
. Фактически, "примитивный" куб соответствует простой импликанте
[
2.6
]
.
Модели последовательностных схем
В качестве функциональной модели последовательностных устройств используется абстрактный конечный автомат
[
2.7
]
, являющийся совокупностью пяти объектов 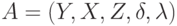 , где
, где 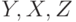 – конечные множества состояний, входных и выходных сигналов соответственно;
– конечные множества состояний, входных и выходных сигналов соответственно;  - функция переходов, определяющая следующее состояние автомата;
- функция переходов, определяющая следующее состояние автомата;  - функция выхода, определяющая выходной сигнал.
- функция выхода, определяющая выходной сигнал.
Различают два типа автомата:
автомат Мили

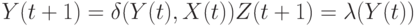
Например,
таблица
2.3представляет конечный автомат Мили с одним входом –  , одним выходом –
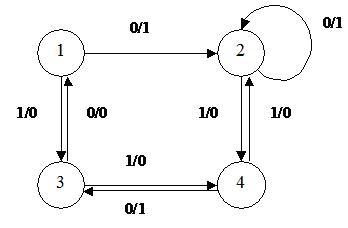
, одним выходом –  и четырьмя состояниями. Здесь на пересечении строки (текущего состояния) и столбца (входного сигнала) приводятся следующее состояние и выходной сигнал автомата.
и четырьмя состояниями. Здесь на пересечении строки (текущего состояния) и столбца (входного сигнала) приводятся следующее состояние и выходной сигнал автомата.
Кроме приведенной табличной формы автомат также часто представляется графом переходов и выходов. Для примера на рис.2.2 показан граф переходов–выходов автомата, представленного табл.2.3 .
Следует отметить, что в этой форме представления неявно предполагается, что функционирование автомата рассматривается в дискретном времени, принимающем целые неотрицательные значения 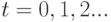 Такие автоматы называются синхронными.
Такие автоматы называются синхронными.
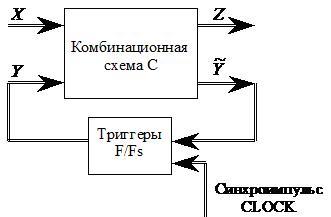
Синхронное последовательностное ДУ имеет каноническую форму представления, приведенную на рис.2.3 . Эта автоматная модель позволяет представить последовательностное устройство в виде комбинационного блока и блока памяти, которые соединены линиями обратной связи 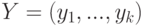 .
.
Здесь каждое состояние в таблице автомата соответствует комбинации переменных состояния -  . Синхронизация неявно реализуется в виде дополнительного входа –
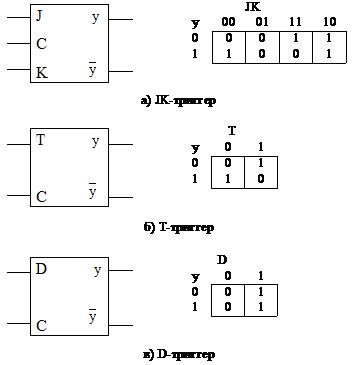
. Синхронизация неявно реализуется в виде дополнительного входа –  . Таким образом события (изменение состояния и выходного сигнала ) инициируются импульсами на входе синхронизации. Состояние схемы запоминается в синхронизируемых триггерах (flip-flop - FF) и изменяется при поступлении импульсов на соответствующий вход. На рис.2.4 представлены три используемые на практике типа синхронизируемых триггеров: JK-триггер, Т-триггер и D-триггер (задержка). В общем случае синхронные ДУ могут иметь несколько входов синхронизации.
. Таким образом события (изменение состояния и выходного сигнала ) инициируются импульсами на входе синхронизации. Состояние схемы запоминается в синхронизируемых триггерах (flip-flop - FF) и изменяется при поступлении импульсов на соответствующий вход. На рис.2.4 представлены три используемые на практике типа синхронизируемых триггеров: JK-триггер, Т-триггер и D-триггер (задержка). В общем случае синхронные ДУ могут иметь несколько входов синхронизации.
Асинхронные последовательностные схемы не имеют входов синхронизации. Их поведение может быть также представлено таблицей переходов и выходов.
Но, в отличие от предыдущего случая, здесь изменение входного сигнала может вызвать цепочку переходов состояний, пока не будет достигнуто стабильное состояние.
Следует отметить, что далеко не все состояния схемы являются стабильными. Например, таблица 2.4представляет асинхронный автомат, в котором стабильные состояния здесь выделены жирным шрифтом.
| x1x2 | ||||
|---|---|---|---|---|
| 00 | 01 | 11 | 10 | |
| 1 | 1,0 | 5,1 | 2,0 | 1,0 |
| 2 | 1,0 | 2,0 | 2,0 | 5,1 |
| 3 | 3,1 | 2,0 | 4,0 | 3,0 |
| 4 | 3,1 | 5,1 | 4,0 | 4,0 |
| 5 | 3,1 | 5,1 | 4,0 | 5,1 |
Для асинхронных последовательных ДУ также часто используется каноническая форма, представленная на рис.c5 (модель Хафмена).