|
Добрый день можно поинтересоваться где брать литературу предложенную в курсе ?Большинство книг я не могу найти в известных источниках |
Сокращение диагностической информации с использованием хеш-функций
Сокращение объема словаря неисправностей при помощи масок обусловлено видом исходного словаря. Так, в зависимости от первоначального словаря неисправностей объем оптимальной общей маски может варьироваться от 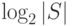 до
до 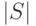 . Экспериментальные результаты, приведенные в предыдущей лекции, показывают, что хотя объем единой маски, полученной жадным алгоритмом меньше
. Экспериментальные результаты, приведенные в предыдущей лекции, показывают, что хотя объем единой маски, полученной жадным алгоритмом меньше 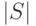 - верхней границы объема оптимальной маски, все же этот объем значительно больше минимальной нижней границы, т. е. величины
- верхней границы объема оптимальной маски, все же этот объем значительно больше минимальной нижней границы, т. е. величины 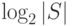 .
.
Для большего сокращения объема словаря неисправностей можно применить различные дополнительные преобразования, в частности хеш-функции [1], с помощью которых для каждой из реакций, хранящейся в СПР, можно получить компактную свертку. Идея применения хеш-функции была высказана Сперанским Д.В. в 70-х годах в одной из его работ по сокращению ДИ, где в качестве такой функции использовалось суммирование по некоторому модулю. Ниже рассматривается несколько других вариантов таких преобразований, предложенных в [1] его учениками.
Обозначим через 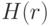 ,
,
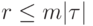 , множество функций вида
, множество функций вида  .
.
Результатом применения функции
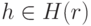 к ДИ, представленной некоторым СПР
к ДИ, представленной некоторым СПР  , назовем матрицу
, назовем матрицу 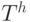 , в которой строка
, в которой строка  ,
,  ,
,
есть результат применения функции  к строке
к строке 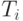 СПР, соответствующей
СПР, соответствующей  -му техническому состоянию ЦУ:
-му техническому состоянию ЦУ:
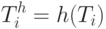
Строку  можно интерпретировать как компактную свертку полной реакции
можно интерпретировать как компактную свертку полной реакции  -ой модификации ДУ, а матрицу
-ой модификации ДУ, а матрицу 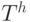 - как результат сокращения ДИ.
- как результат сокращения ДИ.
Из всех функций множества 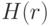 подходящими для сокращения ДИ являются только такие
подходящими для сокращения ДИ являются только такие  , для которых выполняется условие
, для которых выполняется условие
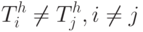 |
( 34.1) |
т. е. которые сохраняют неизменной глубину диагностирования.
Из того, что 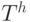 - бинарная матрица, очевидно, что условие (34.1) может выполняться только когда выполняется условие
- бинарная матрица, очевидно, что условие (34.1) может выполняться только когда выполняется условие
 |
( 34.2) |
В качестве меры сокращения ДИ, представленной СПР  , с помощью функции
, с помощью функции 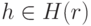 введем величину
введем величину

которую назовем эффективностью сжатия. С учетом (34.2) ясно, что для функции  максимальное значение величины
максимальное значение величины  , соответствующее наилучшему сжатию информации при выполнении условия (34.1), равно 1.
, соответствующее наилучшему сжатию информации при выполнении условия (34.1), равно 1.
В литературе описано множество различных видов хеш-функций и методов их построения [2]. Проведенные авторами работы [1] эксперименты показали целесообразность применения для сокращения ДИ двух разновидностей хеш-функций - полиномиальной (мультипликативной) и позиционной. Преимуществом этих хеш-функций является их простота и высокая скорость вычисления. Дополнительным позитивным фактором, влияющим на выбор этих функций, является наличие единственного (за исключением разрядности результата) параметра, определяющего эти функции.
Полиномиальная хеш-функция 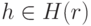 в качестве результата выдает последние
в качестве результата выдает последние  бит значения многочлена
бит значения многочлена 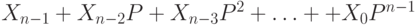 , т. е.
, т. е.
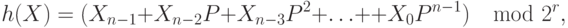
где 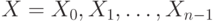 - входной битовый набор (вектор полной реакции ДУ),
- входной битовый набор (вектор полной реакции ДУ),  - параметр хеш-функции, - целое нечетное число из диапазона
- параметр хеш-функции, - целое нечетное число из диапазона 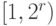 .
.
Для вычисления результата позиционной хеш-функции 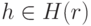 от аргумента
от аргумента  вычисляются значения
вычисляются значения
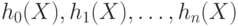
Величина 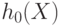 принимается равной нулю, а для определения значения
принимается равной нулю, а для определения значения
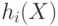 ,
,
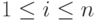 вычисляется величина
вычисляется величина
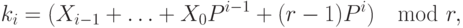
где  - параметр хеш-функции, после чего значение
- параметр хеш-функции, после чего значение 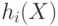 полагается равным h_i(X)=
полагается равным h_i(X)= 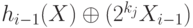 . Здесь
. Здесь  - побитовая операция сложения по модулю 2. В качестве результата хеш-функция
- побитовая операция сложения по модулю 2. В качестве результата хеш-функция 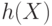 возвращает значение
возвращает значение  .
.
Наряду с хеш-функциями стандартного вида рассмотрим функции, заданные сигнатурными анализаторами различной структуры.
Первое из таких преобразований определим сигнатурным преобразователем, изображенным на рис. 26.3 и заданным соотношением
![h_i=\left [
\begin{array}{ccccc}
c_{r-1}& c_{r-2}&\ldots &c_{1}& c_{0}\\
1& 0 &\ldots &0& 0\\
0& 1 &\ldots &0& 0\\
\vdots& \vdots &\ddots &\vdots & \vdots \\
0& 0 &\ldots &1& 0\\
\end{array}
\right ]
h_{i-1}+\left [
\begin{array}{c} 1\\0\\0\\\vdots\\0 \end{array}
\right ]R_i.](/sites/default/files/tex_cache/f81621dfe51500cce40e43e484a46f37.png) |
( 34.3) |
Здесь  представляет содержимое сдвигового регистра - вектор, состоящий из
представляет содержимое сдвигового регистра - вектор, состоящий из  двоичных значений. В качестве начального содержимого
двоичных значений. В качестве начального содержимого  сдвигового регистра примем нулевое значение.
В этом случае
сдвигового регистра примем нулевое значение.
В этом случае  значений
значений  можно сопоставить разрядами целого числа
можно сопоставить разрядами целого числа  из диапазона
из диапазона 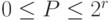 , представленного в двоичной форме.
Результатом преобразования будем считать
, представленного в двоичной форме.
Результатом преобразования будем считать  бит содержимого сдвигового регистра после подачи на вход последовательно всей реакции ДУ.
бит содержимого сдвигового регистра после подачи на вход последовательно всей реакции ДУ.
Другие два преобразования будем задавать аналогичным образом, взяв две разновидности многовходного сигнатурного анализатора, предложенные в [3,4] . На каждом такте на вход таких анализаторов подается сразу  бит выходной реакции ДУ. В таком случае недостающие биты данных при
бит выходной реакции ДУ. В таком случае недостающие биты данных при

будем заполнять нулями.
Одна разновидность такого сигнатурного анализатора задается соотношением
![h_i=\left [
\begin{array}{ccccc}
c_{r-1}& c_{r-2}&\ldots &c_{1}& c_{0}\\
1& 0 &\ldots &0& 0\\
0& 1 &\ldots &0& 0\\
\vdots& \vdots &\ddots &\vdots & \vdots \\
0& 0 &\ldots &1& 0\\
\end{array}
\right ]
h_{i-1}+\left [
\begin{array}{l} R_{(i-1)r+1}\\ R_{(i-1)r+2}\\ R_{(i-1)r+3}\\\vdots\\ R_{ir} \end{array}
\right ].](/sites/default/files/tex_cache/e1d44ee9404af32a69628a71b915b485.png) |
( 34.4) |
а вторая -
![h_i=\left [
\begin{array}{ccccc}
c_{r-1}& c_{r-2}&\ldots &c_{1}& c_{0}\\
1& 0 &\ldots &0& c_{1}\\
0& 1 &\ldots &0& c_{2}\\
\vdots& \vdots &\ddots &\vdots & \vdots \\
0& 0 &\ldots &1& c_{r-1}\\
\end{array}
\right ]
h_{i-1}+\left [
\begin{array}{l} R_{(i-1)r+1}\\ R_{(i-1)r+2}\\ R_{(i-1)r+3}\\\vdots\\ R_{ir} \end{array}
\right ].](/sites/default/files/tex_cache/41d28bfad8ba9dcc4fb16dcd5455453b.png) |
( 34.5) |
Так же как и в предыдущем случае в качестве начального содержимого  сдвигового регистра используется нулевой вектор, а значения
сдвигового регистра используется нулевой вектор, а значения  будем определять как значения двоичных разрядов некоторого целого числа
будем определять как значения двоичных разрядов некоторого целого числа  .
.
Во всех приведенных функциях высокая скорость вычислений достигается за счет простоты выполняемых операций.
В дальнейшем вышеперечисленные хеш-функции будем обозначать в порядке их определения соответственно через 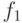 ,
,  ,
, 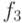 ,
, 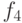 и
и 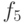 .
.
Как видно из определений, любую из приведенных хеш-функций можно считать заданной, если зафиксирован параметр  . Логично предположить, что не для любого параметра
. Логично предположить, что не для любого параметра  для хеш-функции
для хеш-функции  будет выполняться условие (34.1) и, более того, что выполнение условия (34.1) для хеш-функции для некоторого СПР
будет выполняться условие (34.1) и, более того, что выполнение условия (34.1) для хеш-функции для некоторого СПР  не гарантирует выполнение этого условия для другого СПР.
не гарантирует выполнение этого условия для другого СПР.
Оценим вероятность того, что функция 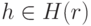 для ДУ с множеством технических состояний
для ДУ с множеством технических состояний  будет удовлетворять условию (34.1). Предположим, что значения хеш-функции
будет удовлетворять условию (34.1). Предположим, что значения хеш-функции  являются равновероятными. Будем получать новые значения хеш-функции последовательно. Получая очередное значение считаем, что все полученные значения различны. Тогда вероятность того, что
являются равновероятными. Будем получать новые значения хеш-функции последовательно. Получая очередное значение считаем, что все полученные значения различны. Тогда вероятность того, что  -е (начиная с нуля) значение функции
-е (начиная с нуля) значение функции  не совпадает ни с одним из полученных ранее, равна
не совпадает ни с одним из полученных ранее, равна 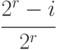 . Таким образом, вероятность того, что для
. Таким образом, вероятность того, что для 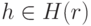 выполняется (34.1), равна величине
выполняется (34.1), равна величине
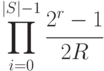 |
( 34.6) |
Зная полученное значение вероятности, можно подсчитать число шагов перебора, которое гарантирует (с вероятностью 99%) получение хеш-функции, обеспечивающей выполнение условия (34.1).
Обозначим это число через  . Значения величины
. Значения величины  для некоторых значений
для некоторых значений 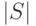 и
и  приведены в табл. 34.1. Здесь
приведены в табл. 34.1. Здесь  ,
,  , - значения
, - значения  для
для  . Как видно из этой таблицы, содержащей информацию о количестве итераций, необходимых для получения хеш-функции, с помощью небольшого перебора вероятнее всего получить хеш-функцию, обеспечивающую эффективность сжатия в диапазоне от 0.58 до 0.67.
. Как видно из этой таблицы, содержащей информацию о количестве итераций, необходимых для получения хеш-функции, с помощью небольшого перебора вероятнее всего получить хеш-функцию, обеспечивающую эффективность сжатия в диапазоне от 0.58 до 0.67.
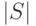 |
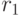 |
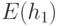 |
 |
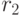 |
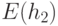 |
 |
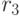 |
 |
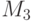 |
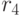 |
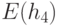 |
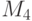 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 100 | 12 | 0.5833 | 14 | 11 | 0.6364 | 52 | 10 | 0.7000 | 681 | 9 | 0.7778 | 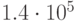 |
| 250 | 13 | 0.6154 | 212 | 12 | 0.6667 | 10776 | 11 | 0.7273 | 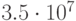 |
10 | 0.8000 | 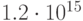 |
| 300 | 15 | 0.6000 | 16 | 14 | 0.6429 | 71 | 13 | 0.6923 | 1174 | 12 | 0.7500 | 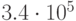 |
| 500 | 15 | 0.6000 | 210 | 14 | 0.6429 | 10094 | 13 | 0.6923 | 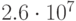 |
12 | 0.7500 | 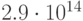 |
| 800 | 17 | 0.5882 | 51 | 16 | 0.6250 | 615 | 15 | 0.6667 | 85895 | 14 | 0.7143 | 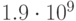 |
| 900 | 17 | 0.5882 | 100 | 16 | 0.6250 | 2271 | 15 | 0.6667 |  |
14 | 0.7143 | 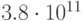 |
| 1100 | 18 | 0.6111 | 45 | 17 | 0.6471 | 468 | 16 | 0.6875 | 49135 | 15 | 0.7333 |  |
| 1500 | 18 | 0.6111 | 337 | 17 | 0.6471 | 25269 | 16 | 0.6875 | 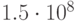 |
15 | 0.7333 |  |
