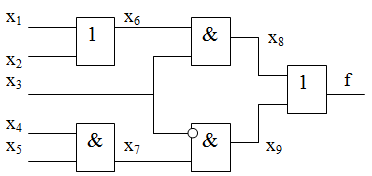НОУ ИНТУИТ | Моделирование, тестирование и диагностика цифровых устройств. Лекция 17: Синтез тестов для заданной неисправности

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Московский государственный университет путей сообщения

Опубликован: 06.09.2012 | Доступ: свободный | Студентов: 1253 / 182 | Оценка: 5.00 / 5.00 | Длительность: 35:22:00

Темы: САПР, Аппаратное обеспечение

Специальности: Разработчик аппаратуры

|

Вам нравится? Нравится 29 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Аннотация: В лекции рассматривается задача построения п проверяющего теста для конкретной заданной неисправности. Изложены аналитические методы построения тестов для комбинационных схем, которые основаны на символьных вычислениях. К ним относятся метод различающей функции и булевых производных. Описан структурный метод активизации одномерных путей.

17. 1 Метод различающей функции

Задача построения проверяющего теста для данной неисправности в комбинационной схеме может быть решена аналитически, если функционирование схемы в исправном и неисправном состояниях задано с помощью аналитических выражений функций выходов.

Пусть f(X) - булева функция, реализуемая исправной комбинационной схемой, а $\varphi (X)$ - булева функция, реализуемая неисправной схемой.

Назовем различающей функцией следующее выражение [17.1]:

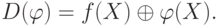
$D(\varphi )=f(X)\oplus \varphi (X).$

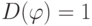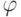Очевидно, что наборы значений входных переменных , на которых $D(\varphi )=1$ , являются проверяющими тестами для данной неисправности $\varphi$ .

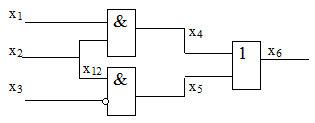
Для примера рассмотрим схему, изображенную на рис. 17.1.

Рис. 17.1. Пример схемы для метода различающей функции

Применим метод различающей функции для построения проверяющего входного набора для константной неисправности 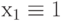$х_{1}\equiv 1$ . В этом случае имеем:

функцию, реализуемую исправной схемой $f(x)=(x_1\&x_2)\vee(x_2\&\overline{x}_3)$ ;
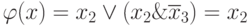функцию, которая реализуется неисправной схемой, $\varphi(x)=x_2\vee(x_2\&\overline{x}_3)=x_2$ .

Тогда различающая функция равна: 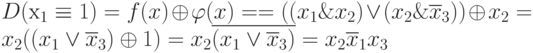$D(х_{1}\equiv 1)=f(x)\oplus \varphi(x)= =((x_1\&x_2)\vee(x_2\&\overline{x}_3)) \oplus x_{2}=x_{2}((x_{1}\vee\overline{x}_3)\oplus 1)=x_2\overline{(x_{1}\vee\overline{x}_3)}=x_2\overline{x}_1x_3$ .

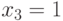Очевидно, что равенство $D(x_{1}\equiv 1)=1$ обеспечивает набор значений входных переменных $x_{1}=0$ , $x_{2}=1$ , $x_{3}=1$ , который и является проверяющим тестом для данной неисправности. Для больших схем этот метод становится слишком громоздким и требует больших вычислительных ресурсов. Однако следует отметить, что современные методы символьных вычислений (над булевыми выражениями) позволяют расширить его возможности.

17.2 Метод булевых производных

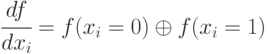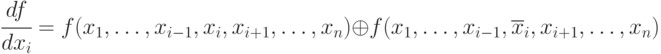Булева производная функции f(X) по переменной $x_{i}$ определяется следующим выражением: $\cfrac{df}{dx_i}=f(x_i=0)\oplus f(x_i=1)$ [17.2]. Существует и другое, эквивалентное приведённому, определение булевой производной: $\cfrac{df}{dx_i}=f(x_1,\ldots,x_{i-1},x_i,x_{i+1},\ldots,x_n)\oplus f(x_1,\ldots,x_{i-1},\overline{x}_i,x_{i+1},\ldots,x_n)$ .

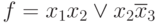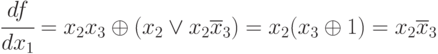Например, для булевой функции $f=x_1x_2\vee x_2\overline{x}_3$ , булева производная $\cfrac{df}{dx_1}= x_2x_3\oplus(x_2\vee x_2\overline{x}_3) = x_{2}(x_{3}\oplus 1) = x_2\overline{x}_3$ .

При вычислении булевых производных сложных функций полезны следующие свойства булевых производных:

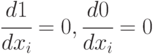$\cfrac{d1}{dx_i}=0, \cfrac{d0}{dx_i}=0$ ;
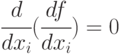$\cfrac{d}{dx_i}(\cfrac{df}{dx_i})=0$ ;
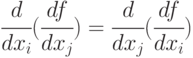$\cfrac{d}{dx_i}(\cfrac{df}{dx_j})=\cfrac{d}{dx_j}(\cfrac{df}{dx_i})$ ;
$\cfrac{d\overline{f}}{dx_i}=\cfrac{df}{dx_i}$ ;
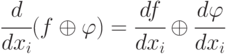$\cfrac{d}{dx_i}(f\oplus\varphi)= \cfrac{df}{dx_i}\oplus\cfrac{d\varphi}{dx_i}$ ;
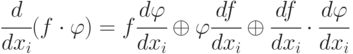$\cfrac{d}{dx_i}(f\cdot\varphi)= f\cfrac{d\varphi}{dx_i}\oplus\varphi\cfrac{df}{dx_i}\oplus\cfrac{df}{dx_i}\cdot\cfrac{d\varphi}{dx_i}$ ;
$\cfrac{d}{dx_i}(f\vee\varphi)=\overline{f}\cfrac{d\varphi}{dx_i}\oplus\overline{\varphi}\cfrac{df}{dx_i}\oplus\cfrac{df}{dx_i}\cdot\cfrac{d\varphi}{dx_i}$ .

Важны следующие частные случаи этих формул для функции , не зависящей от переменной $x_{i}$ :

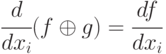$\cfrac{d}{dx_i}(f\oplus g)= \cfrac{df}{dx_i}$ ;
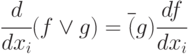$\cfrac{d}{dx_i}(f\vee g)=\overline(g) \cfrac{df}{dx_i}$ ;
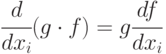$\cfrac{d}{dx_i}(g\cdot f)=g\cfrac{df}{dx_i}$ ;
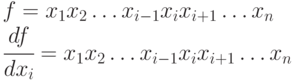для $f=x_1x_2\ldots x_{i-1}x_ix_{i+1}\ldots x_n\\\cfrac{df}{dx_i}= x_1x_2\ldots x_{i-1}x_ix_{i+1}\ldots x_n$ ;
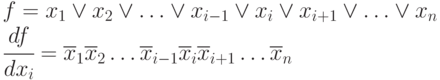
для $f=x_1\vee x_2\vee\ldots\vee x_{i-1}\vee x_i\vee x_{i+1}\vee \ldots\vee x_n\\ \cfrac{df}{dx_i}= \overline{x}_1\overline{x}_2\ldots \overline{x}_{i-1}\overline{x}_i\overline{x}_{i+1}\ldots \overline{x}_n$

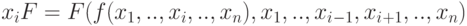На практике важным является дифференцирование сложных функций, когда функция явно не зависит от переменной $x_{i}F = F(f(x_{1},..,x_{i},..,x_{n}),x_{1},..,x_{i}_{-1},x_{i}_{+1},..,x_{n})$ .

В этом случае имеет место $\cfrac{dF}{dx_i}=\cfrac{dF}{df}\cdot\cfrac{df}{dx_i}$ .

Для булевых функций справедливо следующее разложение Тейлора по переменной $x_{i}$ в точке $x_{i}=h_{i}$ с использованием булевой производной:

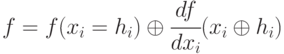
$f=f(x_i=h_i)\oplus\cfrac{df}{dx_i}(x_i\oplus h_i)$

Тогда различающая функция неисправности для 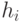$h_{i}$ может быть представлена следующим образом:

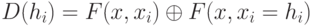$D(h_i)=F(x,x_i)\oplus F(x,x_i=h_i)$ , где $h_{i} =0,1$ .

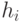Используя разложение Тейлора функции по переменной $x_{i}$ в точке $h_{i}$ , получаем:

$D(h_i)=F(X,x_i=h_i)\oplus\cfrac{dF}{dx_i}(x_i\oplus h_i)\oplus F(X,x_i=h_i)= \cfrac{dF}{dx_i}(x_i\oplus h_i)$

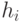Здесь второй сомножитель $(x_i\oplus h_i)$ даёт условие различения сигналов $x_{i}$ и $h_{i}$ в исправной и неисправной схеме на линии . Первый же сомножитель определяет условие распространения рассогласования сигнала в исправной и неисправной схеме до выхода схемы . Это соотношение является основой для метода булевых производных.

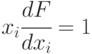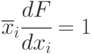Таким образом, для построения теста для константной неисправности $h_{i}\equiv 0$ необходимо решить булево уравнение (найти значения входных переменных) $x_i\cfrac{dF}{dx_i}=1$ , а для неисправности $h_{i}\equiv 1$ - уравнение $\overline{x}_i\cfrac{dF}{dx_i}=1$ .

Рассмотрим метод булевых производных на примере построения теста неисправности 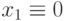$x_{1}\equiv 0$ для схемы рис. 17.2. Для построения теста нам необходимо решить уравнение $x_1\cfrac{df}{dx_1}=1$ .

Рис. 17.2. Иллюстрация метода булевых производных

При вычислениях используем приведенные выше свойства булевых производных и получаем:

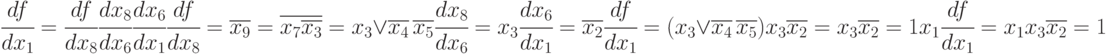
$\cfrac{df}{dx_1}=\cfrac{df}{dx_8}\cfrac{dx_8}{dx_6}\cfrac{dx_6}{dx_1}\\ \cfrac{df}{dx_8}=\overline{x_9}=\overline{x_7\overline{x_3}}=x_3\vee\overline{x_4}\,\overline{x_5}\\ \cfrac{dx_8}{dx_6}=x_3\\ \cfrac{dx_6}{dx_1}=\overline{x_2}\\ \cfrac{df}{dx_1}=( x_3\vee\overline{x_4}\,\overline{x_5})x_3\overline{x_2}= x_3\overline{x_2}=1\\ x_1\cfrac{df}{dx_1}=x_1x_3\overline{x_2}=1$

Из этого выражения следует, что набор значений входов 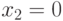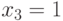$x_{1}=1$ , $x_{2}=0$ , $x_{3}=1$ является проверяющим тестом для данной неисправности.

Рассмотрим построение теста для неисправности $x_{7}\equiv 1$ внутренней линии той же схемы.

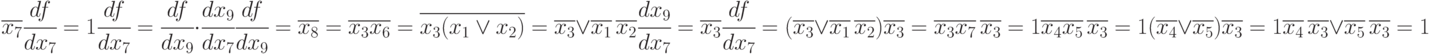
$\overline{x_7}\cfrac{df}{dx_7}=1\\ \cfrac{df}{dx_7}=\cfrac{df}{dx_9}\cdot\cfrac{dx_9}{dx_7}\\ \cfrac{df}{dx_9}=\overline{x_8}=\overline{x_3x_6}=\overline{x_3(x_1\vee x_2)}=\overline{x_3}\vee\overline{x_1}\,\overline{x_2}\\ \cfrac{dx_9}{dx_7}=\overline{x_3}\\ \cfrac{df}{dx_7}=(\overline{x_3}\vee\overline{x_1}\,\overline{x_2})\overline{x_3}=\overline{x_3}\\ \overline{x_7}\,\overline{x_3}=1\\ \overline{x_4x_5}\,\overline{x_3}=1\\ (\overline{x_4}\vee\overline{x_5})\overline{x_3}=1\\ \overline{x_4}\,\overline{x_3}\vee\overline{x_5}\,\overline{x_3}=1$

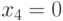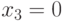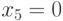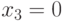Таким образом, для проверки данной неисправности можно использовать наборы $x_{4}=0$ , $x_{3}=0$ или $x_{5}=0$ , $x_{3}=0$ , что следует из последнего выражения для различающей функции.

Дальше >>

Авторизоваться

Моделирование, тестирование и диагностика цифровых устройств

Синтез тестов для заданной неисправности

17. 1 Метод различающей функции

17.2 Метод булевых производных

Вопросы и ответы