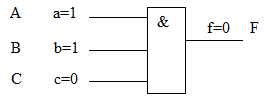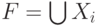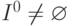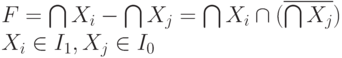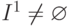|
Добрый день можно поинтересоваться где брать литературу предложенную в курсе ?Большинство книг я не могу найти в известных источниках |
Дедуктивный метод моделирования неисправностей
12.1 Дедуктивный метод моделирования в двоичном алфавите
Вспомним, что основная цель моделирования неисправных цифровых схем заключается в получении списков проверяемых и непроверяемых неисправностей на заданных входных воздействиях. Данный метод работает непосредственно со списками неисправностей, проверяемых на данном входном наборе. Метод основан на анализе логической зависимости значений сигналов на данном входном наборе от присутствия неисправностей [12.1].
Сначала для каждого входного набора выполняется моделирование исправной схемы в двоичном алфавите. А далее для каждой линии схемы (в том числе и внешних выходов) определяются списки неисправностей, при которых значение сигнала меняется на противоположное. Поэтому здесь с каждой линией схемы связывается список неисправностей, изменяющих значения сигналов на этом входе или выходе, как это показано на рис. 11.1 [12.2]. Здесь малыми буквами обозначены переменные значений сигналов, а большими - списки неисправностей, связанные с соответствующими линями. Каждый список содержит неисправности, которые дают значения сигналов на данной линии противоположные значениям сигналов в исправной схеме. Например, для 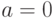 список
список  содержит все неисправности схемы, при которых
содержит все неисправности схемы, при которых 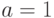 .
.
Основной проблемой в дедуктивном методе является получение списка неисправностей, связанного с выходом логического элемента, по спискам неисправностей его входов[12.3]. При этом неисправности, изменяющие значение выхода элемента, определяются по спискам неисправностей, изменяющих сигналы на его входах, с помощью специальных теоретико-множественных операций, определяемых законом функционирования данного элемента. Существенной особенностью дедуктивного метода является то, что в результате одного шага моделирования, который соответствует подаче данного тестового набора, определяются все неисправности, проверяемые на этом наборе. Шаг моделирования при этом существенно удлиняется. Вычисления проводятся только вдоль путей схемы, по которым распространяется влияние неисправностей.
Основной проблемой является получение теоретико-множественных формул для распространения списков неисправностей через вентиль. То есть, как по данным спискам неисправностей входов вентиля получить список неисправностей, связанный с его выходом. Рассмотрим логический элемент И (рис. 12.1), на входах и выходах которого в исправной схеме на данном тестовом наборе устанавливаются определённые значения 0 или 1 (рассмотрим сначала моделирование в двоичном алфавите).
Рассмотрим первую типовую ситуацию. Пусть 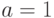 ,
,  ,
, 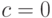 и
и 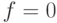 . Тогда неправильное значение
. Тогда неправильное значение  на выходе этого вентиля вызывает любая неисправность из списка
на выходе этого вентиля вызывает любая неисправность из списка  , которая не содержится в списках
, которая не содержится в списках  и
и  .
Поэтому в данном случае при распространении списка неисправностей через данный логический элемент имеем:
.
Поэтому в данном случае при распространении списка неисправностей через данный логический элемент имеем:  (здесь минус - означает вычитание множеств -
(здесь минус - означает вычитание множеств - 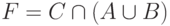 ).
Очевидно, что к полученному списку
).
Очевидно, что к полученному списку  необходимо добавить неисправность
необходимо добавить неисправность 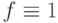 выхода вентиля.
Поэтому окончательное выражение для распространения списков неисправностей в этом случае имеет вид
выхода вентиля.
Поэтому окончательное выражение для распространения списков неисправностей в этом случае имеет вид 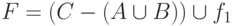 .
.
Рассмотрим вторую типовую ситуацию для этого вентиля, при которой 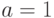 ,
,  ,
, 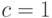 ,
,  . Очевидно, что в этом случае значение
. Очевидно, что в этом случае значение 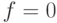 может вызвать любая неисправность из списков
может вызвать любая неисправность из списков 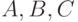 и неисправность
и неисправность 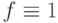 . Поэтому получаем следующее теоретико-множественное правило для распространения неисправностей
. Поэтому получаем следующее теоретико-множественное правило для распространения неисправностей 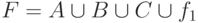 .
В табл. 11.1 в общем виде приведены правила распространения неисправностей для типовых вентилей в стандартных ситуациях. Здесь
.
В табл. 11.1 в общем виде приведены правила распространения неисправностей для типовых вентилей в стандартных ситуациях. Здесь  - множество входов вентиля, имеющих значение 0,
- множество входов вентиля, имеющих значение 0, 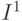 - множество входов вентиля, имеющих значение 1.
- множество входов вентиля, имеющих значение 1.
С помощью полученных правил распространения списков неисправностей выполняется продвижение по схеме от входов к выходам. В результате получается для внешних выходов общий список неисправностей схемы, проверяемых на данном входном наборе. Алгоритм продвижения в общих чертах аналогичен алгоритму событийного моделирования. Но при дедуктивном методе, в отличие от обычного моделирования, должны обрабатываться два вида событий:
- изменение значений сигналов исправной схемы;
- изменение списков неисправностей (при чём оно может быть без изменения значений сигналов).
Рассмотрим данный метод на примере схемы, представленной на рис. 12.2. Очевидно, что для внешних входов схемы связанные с ними списки неисправностей содержат по одной константной неисправности (значения констант противоположны значениям внешних входов). Поскольку мы моделируем схему на входном наборе 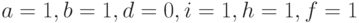 , то получаем:
, то получаем:
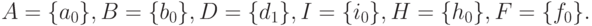
Далее по приведенным выше теоретико-множественным правилам выполняем распространение списков неисправностей со входов схемы до ее внешнего выхода:

Поскольку  является внешним выходом, то полученный список
является внешним выходом, то полученный список  содержит все неисправности, проверяемые данным входным набором.
содержит все неисправности, проверяемые данным входным набором.
Мы уже говорили о том, что в дедуктивном методе используется событийное моделирование. Далее рассмотрим события, вызываемые изменением входа схемы  . Прежде всего, изменяется список
. Прежде всего, изменяется список  . Это изменение вызывает следующие события:
. Это изменение вызывает следующие события:

Очевидно, выполнив эту процедуру для каждого входного набора, мы можем получить список неисправностей, проверяемых всей входной последовательностью, путём объединения списков неисправностей, проверяемых на каждом входном наборе.
При дедуктивном методе моделирования длины списков - переменные, изменяющиеся во времени и при продвижении по схеме. Это обстоятельство ведёт к большим затратам оперативной памяти. Но по быстродействию дедуктивный метод превосходит параллельный для больших схем, содержащих более 1000 логических элементов.