|
Добрый день можно поинтересоваться где брать литературу предложенную в курсе ?Большинство книг я не могу найти в известных источниках |
Модели цифровых устройств
Альтернативные графы (бинарные диаграммы решений)
Бинарные диаграммы решений являются ациклическими ориентированными графами, представляющими булевы функции. Этот тип модели был предложен в
[
2.7
]
и в настоящее время широко используется при моделировании и генерации тестов ЦУ. Множество его вершин можно разбить на три подмножества: внутренние узлы (степень входа равна  , степень исхода равна
, степень исхода равна  ), листья (степень входа равна
), листья (степень входа равна  , степень исхода равна
, степень исхода равна  ) и корень (степень входа равна
) и корень (степень входа равна  , степень исхода равна
, степень исхода равна  ). Логические значения
). Логические значения  или
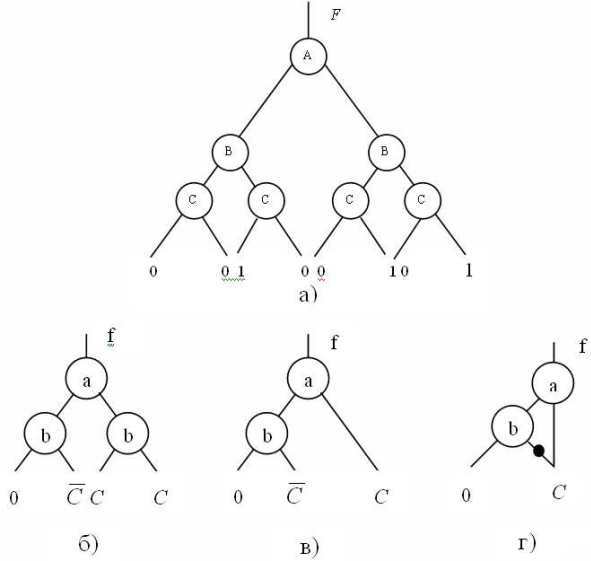
или  , принимаемые булевой функцией, соответствуют листьям диаграммы. Внутренние вершины соответствуют переменным булевой функции. Путь на графе из корневой вершины до одного листа, в зависимости от значений переменных булевой функции, определяет ее значение. Например, на рис.2.6 представлена бинарная диаграмма решений для булевой функции
, принимаемые булевой функцией, соответствуют листьям диаграммы. Внутренние вершины соответствуют переменным булевой функции. Путь на графе из корневой вершины до одного листа, в зависимости от значений переменных булевой функции, определяет ее значение. Например, на рис.2.6 представлена бинарная диаграмма решений для булевой функции  .
.
Для определения значения булевой функции начинаем двигаться из корневой вершины вниз к листьям дерева. При прохождении каждой внутренней вершины, необходимо решить – по какой ветви (левой или правой), в зависимости от значения переменной, соответствующей текущей вершине, мы должны идти дальше. Значение булевой функции ( ) определяется последней вершиной такого пути - висячей вершиной (листом дерева). Допустим, что нам необходимо вычислить значение данной булевой функции c помощью бинарной диаграммы (
рис.
2.6) при следующих значения переменных:
) определяется последней вершиной такого пути - висячей вершиной (листом дерева). Допустим, что нам необходимо вычислить значение данной булевой функции c помощью бинарной диаграммы (
рис.
2.6) при следующих значения переменных:  . Начиная с корневой вершины, при прохождении вершины
. Начиная с корневой вершины, при прохождении вершины  выбираем левую ветвь (так как
выбираем левую ветвь (так как 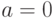 ), далее в вершине
), далее в вершине  также выбираем левую ветвь и попадаем в лист дерева, соответствующий
также выбираем левую ветвь и попадаем в лист дерева, соответствующий  (в данном случае функция не зависит от значения переменной
(в данном случае функция не зависит от значения переменной  ). Следует отметить, что иногда листья дерева могут соответствовать не только константам
). Следует отметить, что иногда листья дерева могут соответствовать не только константам 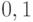 , но и переменным. Так для нашего примера листом является вершина
, но и переменным. Так для нашего примера листом является вершина  , поскольку при
, поскольку при 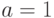 значение функции определяется этой переменной (
значение функции определяется этой переменной (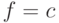 ). Точка соответствует инверсии конечного результата. Например, при
). Точка соответствует инверсии конечного результата. Например, при 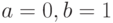 для нашего примера получаем
для нашего примера получаем  . Если при прохождении по графу встречается несколько инверсий (точек), то конечный результат инвертируется в случае их нечетного числа.
. Если при прохождении по графу встречается несколько инверсий (точек), то конечный результат инвертируется в случае их нечетного числа.
Рассмотрим построение бинарной диаграммы из таблицы истинности на примере булевой функции, заданной табл.2.5
[
2.7
]
. Сначала строится полное двоичное дерево, представленное на рис. 2.7 а), где каждый путь от корня до листа соответствует одной строке таблицы истинности. Далее эта диаграмма упрощается следующим образом. Так как обе ветви из левого узла с помечены  , то этот узел можно удалить и заменить его листом, помеченным
, то этот узел можно удалить и заменить его листом, помеченным  . Дальнейший анализ показывает, что остальные узлы
. Дальнейший анализ показывает, что остальные узлы  имеют ветви, помеченные
имеют ветви, помеченные  или
или  (
( или
или  ), и их также можно также удалить и заменить на листья, помеченные
), и их также можно также удалить и заменить на листья, помеченные  или
или 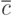 . Дальнейшие упрощения показаны на рис.2.7 б)-в).
. Дальнейшие упрощения показаны на рис.2.7 б)-в).
Структурные модели
Информация о логике функционирования ДУ, которую дают описанные выше функциональные модели , является недостаточной для решения проблем генерации тестов и моделирования. При разработке алгоритмов генерации тестов и моделирования чаще используется структурная модель цифрового устройства, отражающая, кроме логики функционирования ДУ, связи между его компонентами и внешней средой. В качестве структурной модели ДУ, как правило, используется правильная логическая сеть. Логическая сеть или схема - это ориентированный граф, вершинами которого являются логические элементы, входы, выходы и узлы разветвления. Направленные дуги графа отображают соединения сети. Правильная логическая сеть - это сеть, у которой выходы никаких двух элементов не соединены вместе и каждая из функций, реализуемых на выходах ДУ, может быть представлена как функция выхода конечного автомата. Основу сети составляют логические элементы двух типов:
- элементы, функционирование которых описывается булевыми функциями;
- элементы памяти, функционирование которых описывается моделью конечного автомата.
Внешнее описание схемы
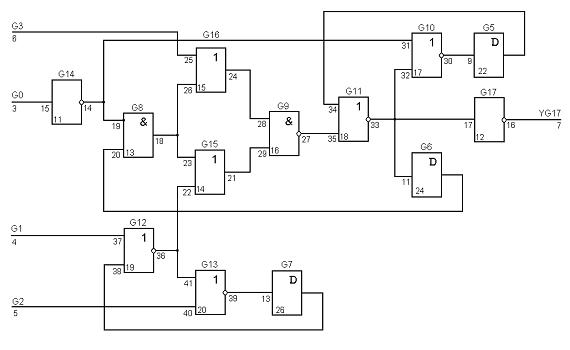
Структурная модель ДУ может быть представлена, например, с помощью простого специализированного языка описания схемы международного каталога ISCAS-89 [6], который позволяет описывать ее входы и выходы, компоненты и связи между ними.
На рис.2.8 представлена логическая схем s27 из каталога ISCAS-89 , описание которой на этом языке приведено на рис.2.9 (сравнив эти рисунки легко освоить данный язык для текстового ввода). Из рис. 2.8 видно, что описание схемы начинается с комментариев (в первой позиции стоит символ 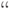 ), содержащих сведения о схеме: число внешних входов, число внешних выходов и D-триггеров, число вентилей по типам. Далее следуют строки описания для каждого элемента схемы, включая внешние входы и выходы. Каждая строка описания содержит:
), содержащих сведения о схеме: число внешних входов, число внешних выходов и D-триггеров, число вентилей по типам. Далее следуют строки описания для каждого элемента схемы, включая внешние входы и выходы. Каждая строка описания содержит:
- имя элемента (для внешних входов
 , а для внешних выходов
, а для внешних выходов  );
); - знак равенства
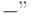 для логических вентилей;
для логических вентилей; - тип вентиля для логических вентилей;
- перечисленные в скобках имена вентилей-предшественников данного элемента, которые позволяют сразу определить количество входов данного вентиля.
Допускаются следующие типы вентилей:
-
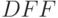 – D-триггер, описание триггеров должно идти непосредственно за описанием внешних входов и выходов схемы;
– D-триггер, описание триггеров должно идти непосредственно за описанием внешних входов и выходов схемы; -
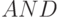 - вентиль И;
- вентиль И; -
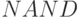 - вентиль НЕ-И;
- вентиль НЕ-И; -
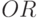 - вентиль ИЛИ;
- вентиль ИЛИ; -
 - вентиль НЕ-ИЛИ;
- вентиль НЕ-ИЛИ; -
 - вентиль сумма по mod2;
- вентиль сумма по mod2; -
 - вентиль равнозначность;
- вентиль равнозначность; -
 - буфер (повторитель).
- буфер (повторитель).
Часто в структурных моделях применяются макроэлементы. При этом элемент описывается в теле макроса, которое используется далее на более высоком уровне. Как правило, допускается несколько уровней вложения, что позволяет использовать иерархический подход к описанию схем.
Кроме связей элементов, в некоторых языках описания может быть представлена информация о временных задержках элементов. Например, это может быть сделано следующим образом:

Это утверждение показывает величину задержки распространения сигнала от входов к выходу данного логического вентиля в некоторых единицах. Текстовое описание схемы S27
Свойства структурных моделей
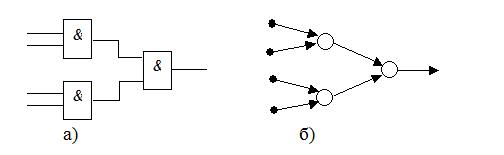
Как было показано выше, структурная модель представляется ориентированным графом, в котором элементы и связи схемы отображаются соответственно в вершины и дуги графа. Внешние входы и выходы схемы при этом отображаются в специальные вершины. Поэтому для исследования свойств структурной модели схемы можно использовать методы теории графов. Например, на рис.2.9 а), б) приведена схема и ее представление ориентированным графом. Отметим, что в данной схеме каждая дуга соединяет только две вершины (сигнал с выхода любого элемента поступает на вход только одного элемента - преемника). Эти схемы не содержат разветвлений (fan out free circuits). Граф такой схемы является деревом.
Схема с разветвлениями представляется двудольным ориентированным графом, который является более общей моделью по сравнению с древовидной структурой. Здесь элементы и связи отображаются в вершины графа таким образом, что каждая дуга соединяет вершину, отображающую элемент схемы, с вершиной, соответствующей связи этого элемента. На рис.2.10 для примера показан такой граф
[
2.7
]
. Здесь вершины, соответствующие связям, отмечены знаком  . Такая модель позволяет представлять схемы с элементами, имеющими несколько выходов, и является более общей.
. Такая модель позволяет представлять схемы с элементами, имеющими несколько выходов, и является более общей.
Следует отметить, что наличие сходящихся разветвлений (reconvergent), как мы увидим дальше в
"Машинные модели логических схем и управление процессом моделирования "
, существенно осложняет построение тестов. На нашем примере
рис.
2.10имеется сходящееся разветвление, содержащее два пути, которое соединяет вершины 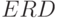 и
и 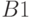 . В схемах, состоящих из простейших вентилей
. В схемах, состоящих из простейших вентилей 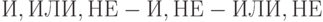 , часто используется понятие четности инверсий пути, которое определяется четностью (суммой по
, часто используется понятие четности инверсий пути, которое определяется четностью (суммой по  ) числа инвертирующих вентилей вдоль данного пути.
) числа инвертирующих вентилей вдоль данного пути.
Уровень логического элемента в комбинационной схеме определяется как мера расстояния этого элемента от внешних входов. При этом внешним входам присваивается уровень, равный  . Далее уровень
. Далее уровень  элемента
элемента  , на входы которого поступают сигналы с выходов элементов
, на входы которого поступают сигналы с выходов элементов 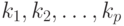 , определяется следующим образом
, определяется следующим образом 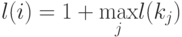
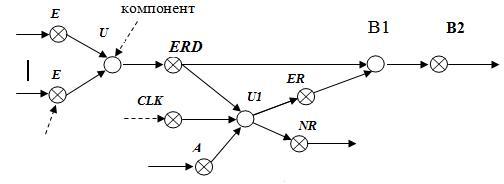
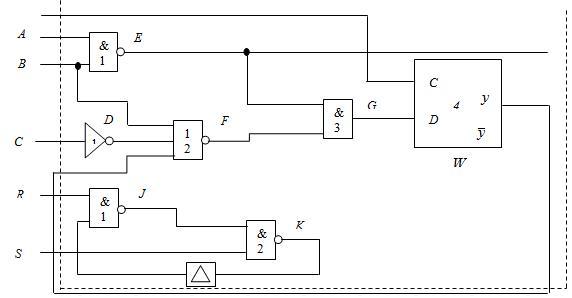
В последовательностной схеме , для вычисления уровней элементов сначала производится условный обрыв линий обратных связей и получившимся псевдовходам присваивается уровень, равный  . Уровни остальных элементов вычисляются по той же формуле. Для примера на рис.2.11 представлена последовательностная схема , в которой уровень
. Уровни остальных элементов вычисляются по той же формуле. Для примера на рис.2.11 представлена последовательностная схема , в которой уровень  имеют элементы
имеют элементы  уровень
уровень  –
– 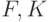 ; уровень
; уровень  –
–  ; уровень
; уровень  –
–  .
.
Иногда вместо явного вычисления уровней используется упорядочивание и нумерация элементов в соответствии с их расстоянием от внешних входов. При этом для любых элементов с номерами 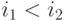 если
если 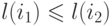 .
.