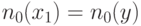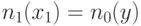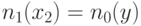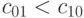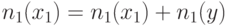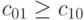Методы генерации тестов PODEM, FAN и SOCRATES

19.3 Метод SOCRATES

Метод SOCRATES (structure-oriented cost-reducing automatic test pattern generation) [19.4] основан на алгоритме FAN с улучшенными процедурами импликации, уникальной активизации путей и кратной процедуры обратного распространения. Кроме этого, в этом алгоритме сокращается число возвратов за счет раннего обнаружения конфликтов и используется несколько эвристик на разных этапах алгоритма, которые также повышают эффективность метода. Кроме этого, в данном методе могут обрабатываться (выступают в роли примитивов - базовых элементов) сложные логические элементы такие как мультиплексоры, сумматоры, кодеры и декодеры, исключающее ИЛИ с произвольным числом входов.

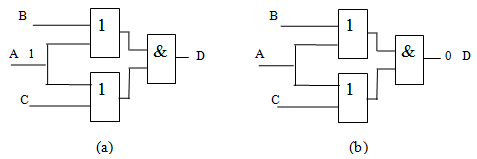
Рассмотрим сначала процедуру импликации на примере схемы рис. 19.9 [19.3].

Рис. 19.9. Импликация в SOCRATES

Здесь входной сигнал 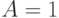(рис. 19.9а)) имплицирует 1 на выходах вентилей ИЛИ и И. С другой стороны, на рис. 19.9b) значение 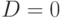имплицирует значение , что следует из тождества контрапозиции импликации 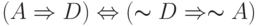, где обозначает дополнение. Из этого следует, что если в процессе обратного распространения выходу вентиля И будет присвоено значение 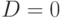, то отсюда вытекает значение входа . Такая импликация, в свою очередь, может привести к раннему обнаружению конфликтов и сокращению числа возвратов при поиске решения.

Для распознавания таких ситуаций перед фазой генерации тестов выполняется фаза обучения. В процессе обучения значение 0 присваивается схеме 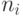с последующей импликацией и анализом результатов. Этот процесс повторяется для значения 1. Предположим, что в процессе импликации 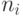инициализируется значением и схема 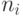принимает значение 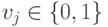в результате выполнения импликации, то есть 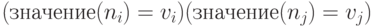. Пусть 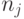управляется вентилем . 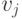Таким образом, если: 1) требует, чтобы все входы имели неконтролирующие значения и 2) прямая импликация дает значени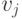е схеме 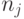, то импликация имеет место. Условие 1) удовлетворяется, если 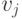имеет значение 0(1) и является вентилем типа И/НЕ -И(ИЛИ/НЕ-ИЛИ) или исключающее ИЛИ. При этом дополнительная функция проверяет отсутствие прямого пути от 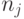к 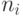. Для комбинационной ранжированной схемы при эта функция дает значение 0. Это подтверждает выполнение условия 2). Возможно, что описанная выше процедура не всегда найдет все возможные импликации, но в целом затраты на этапе обучения окупаются за счет сокращения возвратов в поиске решения.

Уникальная активизация в методе FAN обрабатывает ситуации, где -граница состоит из одного вентиля и все возможные пути -распространения проходят через этот вентиль. В методе SOCRATES улучшена также процедура уникальной активизации.

Определение 19.1. Говорят, что сигнал доминирует над сигналом -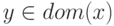, если все ориентированные пути от ко внешним выходам схемы проходят через .

Пусть является единственным в -границе и множество сигналов 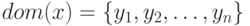- выходы сигналов соответствующих вентилей множества 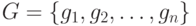. Тогда для всех вентилей неконтролирующие значения присваиваются всем входам , которые могут быть достигнуты из любым путем. Это иллюстрируется на рис. 19.10.

Рис. 19.10. Улучшенная одномерная активизация

Здесь выход вентиля имеет D-значение, который разветвляется на вентили и , которые далее сходятся на вентиле . Очевидно, в этой ситуации сигнал должен быть установлен в неконтролирующее значение .

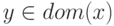Определение 19.2. Сигнал называется непосредственным доминатором сигнала , если и является элементом 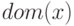с минимальным рангом схемы.

Если непосредственные доминаторы всех сигналов известны, то доминаторы любого сигнала могут быть определены рекурсивно. Например, если сигнал является непосредственным доминатором сигнала , и сигнал является непосредственным доминатором , то сигнал является доминатором .

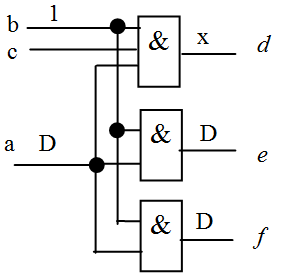
Предложено дополнительное правило для уникальной активизации, которое требуется для обработки ситуаций, представленных на рис. 19.11.

Рис. 19.11. Уникальная активизация кратных путей

Предположим, что сигнал является единственным сигналом D-границы или доминатором такого единственного сигнала. Он разветвляется на три вентиля И, на вход которых поступает сигнал . Кроме этого, один из И вентилей имеет третий вход c. Предположим, что сигнал - единственный сигнал в D-границе, или доминатор такого сигнала и разветвляется на вентили 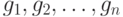, которые все требуют одинаковых неконтролирующих значений - 0 или 1. Если сигнал разветвляется на те же вентили 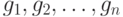, то присваивается неконтролирующее значение.

Кратное обратное распространение в SOCRATES использует тот факт, что некоторые часто встречающиеся схемные конфигурации обрабатываются как примитивы (базовые элементы). Например, это относится к схемам, реализующим исключающее ИЛИ. Важнейшим свойством этого элемента является то, что активизированный путь на входе двухвходового элемента распространяется на его выход независимо от значения второго входа. Например, значения 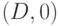дают на выходе значение , а 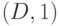соответственно - 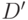. Более того, при распространении через (НЕ) исключающее ИЛИ необходимо только следить за тем, чтобы входы имели определенные значения и не имели одновременно два -значения. Это можно расширить на произвольное число входов элементов исключающее ИЛИ, которые SOCRATES также поддерживает.

Отметим, что метод PODEM не поддерживает исключающее ИЛИ (как примитив) в отличие от -алгоритма, который имеет примитивные -кубы для этого элемента.

Таблица 19.4.

Формулы		Условия

В методе SOCRATES исключающее ИЛИ обрабатывается в соответствии с правилами, представленными в табл. 19.4. Здесь 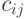представляют значения управляемости, которые отражают сложность установки в и в для , где и - входы для двухвходового вентиля исключающего ИЛИ и - его выход. Этот подход можно использовать и для других примитивов высокого уровня, для которых получены соответствующие формулы. Основное преимущество этих примитивов лежит в сокращении числа разветвлений (потенциальных конфликтов). Но иногда это можно реализовать и на вентильном уровне. Например, если двухвходовой мультиплексор имеет 1 на обоих входах данных, то выходу следует установить значение 1 даже при наличии неопределенного значения на управляющем входе.

Ключевые термины:

D-распространение - распространение в схеме символов , , 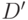характеризующих различие значений сигналов в исправной и неисправной схеме.

Обратное распространение (продвижение назад) - процедура поиска значений сигналов, обеспечивающих значения сигналов для элементов, находящихся ближе к выходам. Выполняется в обратном порядке: от выходов ко входам.

Прямая импликация - процедура снятия неопределённости на линиях схемы, выполняемая в прямом порядке от входов к выходам.

Обратная импликация - процедура снятия неопределённости на линиях схемы, выполняемая в обратном порядке от выходов ко входам.

Краткие итоги

В лекции продолжено рассмотрение задачи построения проверяющего теста для конкретной заданной неисправности с использованием 6-значного алфавита.

В "Методы генерации тестов PODEM, FAN и SOCRATES" изложен метод PODEM, разработанный первоначально для схем контроля четности и основанный на другой по сравнению с -алгоритмом стратегии поиска решений. Представлены основные этапы построения теста этим методом, включающие распространение назад, прямую импликацию и перебор возможных решений в случае возникновения конфликта.

В "Методы генерации тестов PODEM, FAN и SOCRATES" представлен метод- FAN, который является развитием метода и использует улучшенные процедуры кратного продвижения назад и уникальной активизации путей.

В "Методы генерации тестов PODEM, FAN и SOCRATES" описан метод SOCRATES, являющийся развитием предыдущего метода FAN за счет улучшения процедур обратного распространения, импликации, уникальной активизации и использования более крупных примитивов.

Вопросы и упражнения

1. Чем отличается метод PODEM от -алгоритма?
2. Опишите процедуру продвижения назад в методе PODEM.
3. Что такое "тяжелый" и "легкий" вход?
4. Как определяется цель в методе PODEM?
5. Как обрабатывается конфликт в методе PODEM?
6. Приведите общий алгоритм PODEM.
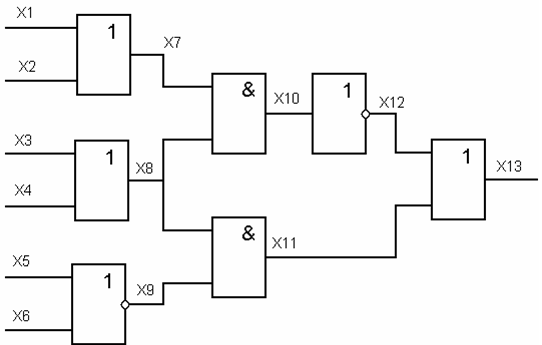
7. Постройте тест методом PODEM для неисправности 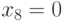приведенной ниже схемы рис. 19.12.
   

   
   Рис. 19.12. Схема для упражнения 7, 12
8. Чем отличается метод FAN от PODEM?
9. Чем отличается процедура кратного продвижения назад?
10. Опишите улучшения в импликации по сравнению с предыдущими методами.
11. Прокомментируйте псевдокод алгоритма FAN.
12. Постройте тест методом FAN для неисправности const.0 выхода второго вентиля первого уровня приведенной ниже схемы рис. 19.12.

    Чем отличается метод SOCRATES от метода FAN?
13. Приведите пример уникальной активизации.
14. В чем суть фазы обучения?
15. Приведите пример функционального примитива.
16. Что дает использование более крупных примитивов?