Влияние стратегий наблюдения выходных сигналов на построение тестов для схем с памятью

24.4 Конъюнктивная форма различающей функции

Кроме введенной авторами дизъюнктивной формы РФ для последовательностных схем используется и конъюнктивная форма РФ [24.5], которая определяется следующим образом:

( Y_н,t)])

В отличие от предыдущей формы здесь выделяются неразличимые пары состояний исправной и неисправной схемы, которые для входной последовательности 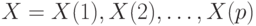дают одинаковые выходные реакции для всех выходов и всех моментов времени.

Как и в предыдущей форме при реализации вычислений вводится вспомогательная (текущая) различающая функция 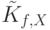, которая при инициализации получает единичное значение. Далее в процессе символьного моделирования она последовательно умножается на каждом шаге на дизъюнктивный терм, соответствующий своему моменту времени,

В этом случае неисправность 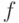является обнаружимой относительно стратегии кратного наблюдения, если и только если 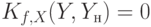для данной входной последовательности . Это означает, что нет пар состояний исправной и неисправной схемы, которые выдают одинаковые выходные реакции.

Для нашего примера для первого момента времени имеем

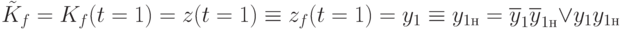
Для второго такта функция имеет вид

что дает .

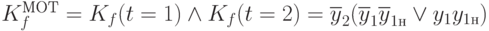Для третьего такта имеем ,

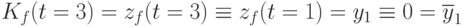откуда следует .

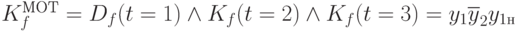Наконец для 4-го такта получаем ,

откуда получаем .

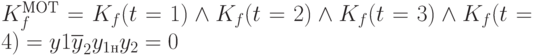Следует отметить, что в случае конъюнктивной формы соответствие различающей функции с узлами обратного различающего дерева более очевидно. Это обусловлено тем, что в ОРД неразличимые множества пар состояний содержат пары, имеющие одинаковые выходные реакции на данную входную последовательность. Но конъюнктивная форма выделяет именно такие пары состояний для входной последовательности.

Так для нашего примера правый узел 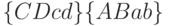ОРД первого уровня соответствует функции 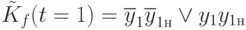. При этом множеству неразличимых пар 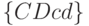соответствует терм 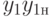, а множеству 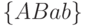- терм 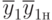. Аналогично правому узлу второго уровня ОРД 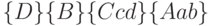соответствует функция

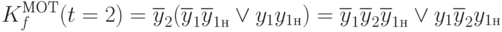
где терм соответствует множеству 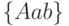и терм - множеству 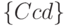. Заметим, что для множеств 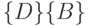, не содержащих неразличимых пар состояний, в функции нет соответствующих термов.

Как и в предыдущем случае, равенство говорит о том, что различающая функция не содержит ни одной неразличимой пары состояний исправной и неисправной схемы и поэтому неисправность 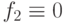схемы рис.1 проверяется входной последовательностью 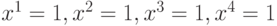относительно кратной стратегии наблюдения.

Фактически конъюнктивная форма различающей функции позволяет свести задачу построения проверяющей последовательности для заданной неисправности схемы с памятью к решению задачи ваыполнимости булевой функции . При решении уравнения можно использовать достаточно развитые алгоритмы решения (SAT) задачи проверки выполнимости булевых функций, в частности, основанные на символьном моделировании [24.6].

Следует отметить, что для последовательностных схем количество неисправностей, непроверяемых относительно одиночной (обычной) стратегии наблюдения выходных сигналов, может быть достаточно большим. Так, например, для схем каталога ISCAS89 даже для одиночных константных неисправностей число таких неисправностей по некоторым данным [24.4,24.5] в среднем достигает 38%. Предложенный аналитический подход и стратегия кратного наблюдения выходных сигналов позволяет существенно повысить полноту проверяющих тестов для схем с памятью, но требует значительных вычислительных ресурсов.

Предлагаемый подход позволяет свести задачу построения проверяющих схем для схем с памятью к решению стандартных задач поверки тавтологии или выполнимости булевых функций (SAT). При решении этих задач можно использовать различные достаточно развитые методы, в частности, генетические алгоритмы.

Ключевые термины:

Стратегия одиночного наблюдения выходов (SOT - single observation time strategy) - определяет, что неисправность считается обнаружимой, если найдется (по крайней мере один) момент времени (такт) такой, что для любой пары состояний 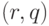исправной и неисправной схем некоторый -й выход имеет различные значения в исправной и неисправной схеме.

Стратегия кратного наблюдения выходов (MOT - multiple observation time strategy) - определяет, что неисправность называется проверяемой, если для каждой пары состояний исправной и неисправной схемы существует свой момент времени, в котором они дают различные выходные сигналы.

Символьное моделирование - для каждой линии схемы в отличие от логического моделирования, которое дает значение сигнала в определенном алфавите, строит булеву функцию, которая зависит от булевых переменных.

Дизъюнктивная форма - нормальная форма, в которой булева формула имеет вид дизъюнкции нескольких конъюнкций литералов.

Конъюнктивная форма - нормальная форма, в которой булева формула имеет вид конъюнкции нескольких дизъюнкций литералов.

Краткие итоги

В лекции рассмотрены основные стратегии наблюдения выходных сигналов, которые используются при построении проверяющих тестов для схем с памятью. Изложены методы, основанные на построении различающей функции для последовательностных схем.

В "Влияние стратегий наблюдения выходных сигналов на построение тестов для схем с памятью" определяются две осноные стратегии наблюдения выходных сигналав, используемых при построении тестов для последовательностных схем: 1) стратегия одиночного наблюдения; 2) стратегия кратного наблюдения.

В "Влияние стратегий наблюдения выходных сигналов на построение тестов для схем с памятью" рассматривается символьное моделирование последовательностных схем, которое в отличие от обычного логического моделирования позволяет для каждой линии схемы построить булеву функцию, которая определяет зависимость от переменных состояний исправной и неисправной схемы.

В "Влияние стратегий наблюдения выходных сигналов на построение тестов для схем с памятью" вводится дизъюнктивная форма различающей функции для последовательностных схем, устанавливается соответствие между термами этой формы и узлами обратного различающего дерева. Показано, что задача построения проверяющих тестов сводится к задаче проверки тавтологии различающей функции.

В "Влияние стратегий наблюдения выходных сигналов на построение тестов для схем с памятью" вводится конъюнктивная форма различающей функции для последовательностных схем, устанавливается соответствие между термами этой формы и узлами обратного различающего дерева. Показано, что задача построения проверяющих тестов сводится к задаче выполнимости различающей функции.

Вопросы и упражнения

1. Дайте определение различающей функции заданной неисправности для многовыходной комбинационной схемы.
2. Дайте определение проверяемости неисправности согласно стратегии одиночного наблюдения выходных сигналов.
3. Дайте определение проверяемости неисправности согласно стратегии кратного наблюдения выходных сигналов.
4. Чем отличаются одиночная и кратная стратегия наблюдения выходных сигналов?
5. Приведите пример неисправности, проверяемой относительно одиночной стратегии наблюдения выходных сигналов.
6. Приведите пример неисправности, непроверяемой относительно одиночной стратегии наблюдения выходных сигналов.
7. Приведите пример неисправности, непроверяемой относительно одиночной стратегии, но проверяемой относительно кратной стратегии наблюдения выходных сигналов.
8. Как строится дизъюнктивная различающая функция для данной неисправности последовательностной схемы.
9. Покажите соответствие термов дизъюнктивной различающей функции и узлов обратного различающего дерева.
10. К чему сводится построение проверяющей последовательности на основе дизъюнктивной различающей функции.
11. Приведите пример построения тестовой последовательности на основе дизъюнктивной различающей функции.
12. Как строится конъюнктивная различающая функция для данной неисправности последовательностной схемы.
13. Покажите соответствие термов конъюнктивной различающей функции и узлов обратного различающего дерева.
14. К чему сводится построение проверяющей последовательности на основе конъюнктивной различающей функции.
15. Приведите пример построения тестовой последовательности на основе конъюнктивной различающей функции.
16. Что дает использование кратной стратегии наблюдения при построении тестов?
17. Какие преимущества и недостатки использовании кратной стратегии наблюдения выходных сигналов?