НОУ ИНТУИТ | Классические и квантовые вычисления. Лекция 1: Решения задач

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Московский государственный университет имени М.В.Ломоносова

Опубликован: 15.03.2007 | Доступ: свободный | Студентов: 611 / 26 | Оценка: 5.00 / 4.50 | Длительность: 19:30:00

Тема: Алгоритмы и дискретные структуры

Специальности: Программист

|

Вам нравится? Нравится 10 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Из раздела 10

10.1 Утверждение задачи вытекает из следующей леммы, которая будет полезна и в дальнейшем.

Лемма. Физически реализуемые преобразования матриц плотности имеют вид

$\rho\mapsto\sum_{m=1}^{s} A^{\ms}_m\rho{}A^\dagger_m, \qquad \sum_{m}^{} A^\dagger_m A^{\ms}_m= I,$

( *)

который будем называть разложением в операторную сумму. А всякое разложение в операторную сумму можно представить в виде $\rho\mapsto$ $\mapsto\Tr_\calF(V\rho{}V^\dagger)$ , где

— изометрическое вложение.

Доказательство. План доказательства следующий:

докажем, что изометрическое вложение и взятие частичного следа имеют разложение в операторную сумму;
докажем, что операторные суммы замкнуты относительно композиции;
найдем представление произвольной операторной суммы в виде $\rho$ $\mapsto\Tr_\calF(V\rho V^\dagger)$ .

Условие изометричности вложения записывается как $V^\dagger V=I$ . Это означает, что изометрическое вложение представимо в виде операторной суммы из одного слагаемого.

Для частичного следа имеется следующее разложение в операторную сумму:
$\begin{equation*} \Tr_\calF(\rho) = \sum_{m}W_m^{\vdag}\rho W_m^\dagger,\quad\, \text{где}\ W_m=I_{\calN}\otimes\bra{m}\colon\, \calN\otimes\calF\to\calN. \end{equation*}$ ( **)
Заметим, что $W_m\bigl(\ket{j,k}\bigr)=\delta_{mk}\ket{j}$ , а $W_m^\dagger\bigl(\ket{j}\bigr)=\ket{j,m}$ .
Пусть $\sum\limits_{m}^{}A^{\vdag}_m\rho A_m^\dagger$ , $\sum\limits_{k}^{}B^{\ms}_k\rho B_k^\dagger$ — разложения двух преобразований в операторные суммы. Тогда их композиция также разлагается в операторную сумму:
$\begin{align*} &\sum_{k}^{}B_k\Big(\sum_{m}^{}A^{\ms}_m\rho {}A_m^\dagger\Big) B_k^\dagger= \sum_{k,m}^{}(B_kA_m)\rho(B_kA_m)^\dagger,\\ &\sum_{k,m}^{}(B_kA_m)^\dagger(B_kA_m)= \sum_{m}^{} A_m^\dagger\Big(\sum_{k}^{}B_k^\dagger B^{\ms}_k\Big) A_m=\sum_{m}^{}A_m^\dagger{}A^{\ms}_m=I. \end{align*}$
Пусть преобразование разложено в операторную сумму , а $\calF$ — -мерное пространство, базисные векторы в котором обозначим $\ket{m}$ . Отображение
$V=\sum_{m}A_m\otimes\ket{m}\colon\ \ket\xi\mapsto\sum_{m} A_m\ket{\xi}\otimes\ket{m}$
является изометрическим вложением, поскольку
$V^\dagger V=\sum_{l,m}\bigl(A_l^\dagger\otimes\bra{l}\bigr) \bigl(A^{\ms}_m\otimes\ket{m}\bigl)= \sum_{l,m} A_l^\dagger{}A^{\ms}_m\ket{k}\cdot\langle l|m\rangle = I.$
Осталось заметить, что операторная сумма представляется в виде $\rho$ $\mapsto\Tr_\calF(V\rho{}V^\dagger)$ . Действительно,
$\Tr_\calF(V\rho{}V^\dagger) = \sum_{m,l} \Tr_\calF\Bigl( A^{\ms}_m\rho{}A_l^\dagger\otimes \ket{m}\bra{l} \Bigr) = \sum_{m} A^{\ms}_m\rho{}A_m^\dagger.$

10.2 Пусть $\rho\in\LL(\calN\otimes\calF)$ , $U\ket{j}=\ket{\xi_j}$ , $Y\ket{k}=\ket{\eta_k}$ . Тогда

$\begin{align*} &\Tr_\calF\left((U\otimes Y)\rho(U\otimes Y)^\dagger\right)=\\ =&\Tr_\calF\Big((U\otimes Y) \sum_{j,k,j',k'}^{}\rho_{jkj'k'}\ket{j,k}\bra{j',k'}\, (U\otimes Y)^\dagger \Big)=\\ =& \Tr_\calF\Big( \sum_{j,k,j',k'}^{}\rho_{jkj'k'}\ket{\xi_j}\bra{\xi_{j'}} \otimes \ket{\eta_k}\bra{\eta_{k'}} \Big)=\sum_{jj'k}^{}\rho_{jkj'k}\ket{\xi_j}\bra{\xi_{j'}}=\\ =&\;U(\Tr_\calF\rho)U^\dagger. \end{align*}$

10.3 Пусть $\sum_{m}^{}\ds A^{\ms}_m\rho{}A_m^\dagger$ — разложение в операторную сумму преобразования (см. задачу 10.1). Тогда

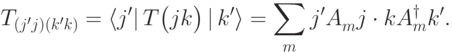
$T_{(j'j)(k'k)}= \langle j'|\, T\big(\ket{j}\bra{k}\big)\,|\, k'\rangle = \sum_{m}^{} \bra{j'}A^{\ms}_m\ket{j}\cdot\bra{k}A_m^\dagger\ket{k'}.$

Такое представление позволяет легко проверить сформулированные в условии задачи свойства а)—в).

Свойство а):

$\sum_{k'}^{}T_{(k'j)(k'k)}= \sum_{k'm}^{}\bra{k'}A^{\ms}_m\ket{j}\cdot\bra{k}A_m^\dagger\ket{k'}=\\ &&=&\sum_{k'm}^{}\bra{k}A_m^\dagger\ket{k'}\bra{k'}A^{\ms}_m\ket{j}= \sum_{m}^{}\bra{k}A_m^\dagger{}A^{\ms}_m\ket{j}=\langle k|j\rangle .$

Свойство б):

$T^*_{(j'j)(k'k)}=\sum_{m}^{} \big(\bra{j'}A^{\ms}_m\ket{j}\bra{k}A_m^\dagger\ket{k'}\big)^*= \\ &&=&\sum_{m}^{}\bra{j}A_m^\dagger\ket{j'}\bra{k'}A^{\ms}_m\ket{k} =T^{\ms}_{(k'k)(j'j)}.$

Свойство в):

$\sum_{j',j,k',k}^{}T_{(j'j)(k'k)}\ket{j',j}\bra{k',k}= \sum_{m}^{}\ket{\psi_m}\bra{\psi_m},$

где

$\ket{\psi_m}=\sum_{j',j}\bra{j'}A_m\ket{j}\,\ket{j',j}.$

И наоборот, всякий неотрицательный оператор можно представить в виде $T =\sum_{m}^{}\ket{\psi_m}\bra{\psi_m}$ , где $\ket{\psi_m}$ — подходящим образом нормированные собственные векторы , отвечающие положительным собственным числам. Обозначим

$\begin{align*} &\ket{\psi_m}=\sum_{m,j',j}^{}a_{mj'j}\ket{j',j},& &A_m\colon\ket{j}\mapsto\sum_{j'}^{}a_{mj'j}\ket{j'}, \end{align*}$

тогда $T_{(j'j)(k'k)}=\sum\limits_{m}^{}a^{\ms}_{mj'j}a^*_{mk'k}$ . Из условия $\sum\limits_{k'}^{}T_{(k'j)(k'k)}=\delta_{jk}$ следует

$\begin{multiple} &\hbox to\textwidth{\displaystyle\langle k|\, \Big( \sum_{m}^{}A_m^\dagger{}A^{\ms}_m\Big)\,|j\rangle = \langle k|\, \Big(\sum_{m,k'}a^*_{mk'k}a^{\ms}_{mk'j} \Big)\,|j\rangle= \sum_{k'}T_{(k'j)(k'k)}=\delta_{jk}.} \end{multiple}$

Осталось проверить, что $T\big(\ket{j}\bra{k}\big)=\sum_{m}^{}A^{\ms}_m\ket{j}\bra{k}A_m^\dagger$ :

$\begin{align*} \sum_{m}^{}A^{\ms}_m\ket{j}\bra{k}A_m^\dagger =&\sum_{j',k'}^{}\sum_{m}^{}a^{\ms}_{mj'j}a^*_{mk'k} \ket{j'}\bra{k'} = \sum_{j'k'}^{}T_{(j'j)(k'k)}\ket{j'}\bra{k'}=\\ =&\; T\big(\ket{j}\bra{k}\big). \end{align*}$

10.4 Свойства а) и б) эквивалентны свойствам а) и б) из предыдущей задачи.

Пусть есть физически реализуемое преобразование матриц плотности $T\colon\rho\mapsto\Tr_\calF(V\rho V^\dagger)$ . Тогда $T\otimes I_{\LL(\calG)}\colon \rho\mapsto\Tr_\calF\bigl((V\otimes I_{\calG})\rho (V\otimes I_{\calG})^\dagger\bigr)$ также является физически реализуемым преобразованием и поэтому обладает разложением в операторную сумму. Следовательно, $T\otimes I_{\LL(\calG)}$ переводит неотрицательные операторы в неотрицательные.

Для доказательства утверждения в другую сторону выведем из свойства в) данной задачи свойство в) предыдущей задачи.

Чтобы доказать неотрицательность матрицы 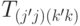$T_{(j'j)(k'k)}$ по парам индексов, взятых в скобки, покажем, что она является матрицей оператора вида $(I\otimes T)\ket\psi\bra\psi$ , где $\ket\psi\in \calN\otimes\calN$ имеет вид $\ket\psi=\sum_{j}^{}\ket{j}\otimes\ket{j}$ . Действительно,

$(I\otimes T)\ket\psi\bra\psi = \sum_{j',j,k',k}^{}T_{(j'j)(k'k)}\ket{j}\bra{k}\otimes\ket{j'}\bra{k'}= \sum_{j',j,k',k}^{}T_{(j'j)(k'k)}\ket{j'j}\bra{k'k}.$

10.5 Воспользуемся результатом задачи 10.1. Представим 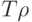$T\rho$ в виде $\Tr_{\calF'}(V\rho{}V^\dagger)$ . Возьмем $\ket\psi\in\calN$ . Поскольку состояние

$\begin{align*} &\Tr_{\calF\otimes\calF'}\bigl(\ket{V\psi}\bra{V\psi}\bigr) = \Tr_\calF\bigl(\Tr_{\calF'}\bigl(V\ket{\psi}\bra{\psi}V^\dagger\bigr)\bigr)= \Tr_\calF\bigl(T\ket\psi\bra\psi\bigr)= \ket\psi\bra\psi \end{align*}$

чистое, $\ket{V\psi}=\ket{\psi,\xi(\psi)}$ (это следует из замечания, сделанного после формулировки задачи 9.2). Из линейности

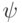следует, что $\ket{\xi(\psi)}=\ket\xi$ не зависит от $\ket\psi$ . Поэтому $TX=X\otimes\gamma$ , где $\gamma=\Tr_{\calF'}(\ket\xi\bra\xi)$ .

10.6 Будем считать, что сразу же после измерения измеряемые q-биты выбрасываются в "мусорную корзину". Это соответствует преобразованию двух квантовых битов в классические:

$T\colon\rho\mapsto\sum_{a,b}\langle\xi_{ab}|\rho|\xi_{ab}\rangle(a,b).$

Чтобы реализовать преобразование

, нужно сначала подействовать унитарным оператором

$H[1]\Lambda(\sx)[1,2]\colon\, \ket{\xi_{ab}}\mapsto\ket{b,a},$

а затем произвести измерение в базисе $\{\ket{0},\ket{1}\}$ ; после этого q-биты выбрасываются.

Без ограничения общности, первый q-бит находится в чистом состоянии $\ket\psi=z_0\ket0+z_1\ket1$ . (Если мы построим восстанавливающую процедуру для чистых состояний, то она по линейности будет продолжаться на смешанные). На третий q-бит измерение не действует, поэтому можно записать

$\bigl(T\otimes I_{\LL(\BB)}\bigr) \Bigl(\ket\psi\bra\psi\otimes \ket{\xi_{00}}\bra{\xi_{00}}\Bigr) = \sum_{a,b}^{}\bigl(a,b, \ket{\psi_{ab}}\bra{\psi_{ab}}\bigr),$

где $\ket{\psi_{ab}}=\bigl(\bra{\xi_{ab}}\otimes I_\BB\bigr) \bigl(\ket\psi\otimes\ket{\xi_{00}}\bigr)$ . Здесь $\bra{\xi_{ab}}$ рассматривается как оператор $\BB^{\otimes2}\to\CC$ , поэтому $\bra{\xi_{ab}}\otimes I_\BB\colon\BB^{\otimes3}\to\BB$ . Заметим, что квадрат нормы вектора $\ket{\psi_{ab}}$ равен вероятности получения пары (a,b)

.

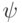Теперь запишем явное выражение для $\ket{\psi_{ab}}$ :

$\begin{align*} &\ket{\psi_{ab}} = \frac{1}{\sqrt2}\sum_{d}^{} \bigl(\bra{\xi_{ab}}\otimes I_\BB\bigr) \bigl(\ket\psi\otimes\ket{d,d}\bigr) =\frac{1}{\sqrt2}\sum_{d} \bra{\xi_{ab}}\psi,d\rangle\,\ket{d}=\\ &=\frac{1}{\sqrt2}\sum_{c,d} z_c \bra{\xi_{ab}}c,d\rangle\,\ket{d} =\frac{1}{2}\sum_{c,d}^{}(-1)^{bc} \delta_{c\oplus a,d} z_c\ket{d}= \frac{1}{2}\sum_{c}^{}(-1)^{bc} z_c\ket{a\oplus c}. \end{align*}$

Из этого выражения сразу следует, что

$\left(\sz\right)^b\left(\sx\right)^a\ket{\psi_{ab}}=\frac{1}{2}\ket\psi.$

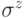Так что состояние $\ket\psi$ в третьем q-бите получится применением операторов $\sigma^x$ и $\sigma^z$ с классическим управлением: управляющими параметрами являются измеренные значения

и

.

Рис. 15.9.

Схема квантовой телепортации изображена на рис. 15.9. Значком $\heartsuit$ обозначен первый бит,— второй (q-бит Алисы),— третий (q-бит Боба). Когда Алиса хочет передать q-бит $\heartsuit$ Бобу, она совершает измерения над ним и своим q-битом (дальше эти q-биты не используются, и она выбрасывает их в мусорную корзину). Результаты измерений она сообщает Бобу по классическому каналу связи (телефону). Боб, используя сообщение Алисы, превращает свой q-бит в q-бит $\heartsuit$ .

Дальше >>

Авторизоваться

Классические и квантовые вычисления

Решения задач

Из раздела 10

Вопросы и ответы