НОУ ИНТУИТ | Классические и квантовые вычисления. Лекция 8: Определение квантового вычисления. Примеры

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Московский государственный университет имени М.В.Ломоносова

Опубликован: 15.03.2007 | Доступ: свободный | Студентов: 616 / 27 | Оценка: 5.00 / 4.50 | Длительность: 19:30:00

Тема: Алгоритмы и дискретные структуры

Специальности: Программист

|

Вам нравится? Нравится 11 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Аннотация: В лекции дается подробное описание квантовых вычислений, приводится определение функции голосования, дается определение универсальной переборной задачи в классической и квантовой постановке, вводится понятие универсальной квантовой схемы, рассматриваются квантовые алгоритмы и класс BQP.

Ключевые слова: определение, функция, вероятность, компьютер, длина, NP, черный ящик, базисными векторами, матричная форма, гиперплоскость, булева функция, полином, машина Тьюринга, суперпозиция

Пока мы описали работу квантового компьютера. Теперь пора определить, когда эта работа приводит к решению интересующей нас задачи. Определение будет похоже на определение вероятностного вычисления.

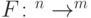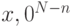Пусть есть функция $F\colon\cb^n\to\cb^m$ . Рассмотрим квантовую схему, работающую с битами: $U=U_L\cdot\ldots\cdot U_2U_1\colon{} \BB^{\otimes N}\to\BB^{\otimes N}$ . Неформально говоря, эта схема вычисляет , если после применения к начальному состоянию $\ket{x,0^{N-n}}$ , мы, "посмотрев" на первые битов, с большой вероятностью "увидим" F(x) . (Остальные q-биты могут содержать произвольный мусор.)

Нужно только оговорить, что такое эта вероятность. Слова "посмотрев" и "увидим" в точном смысле означают, что производится измерение значений соответствующих q-битов. В результате измерения могут получаться разные ответы, каждому соответствует своя вероятность. Ниже (раздел 9) этот вопрос рассматривается подробно. Для того, чтобы дать определение квантового вычисления функции , достаточно (не вдаваясь в обсуждение физических объяснений этого факта) принять следующее: вероятность получения базисного состояния, при измерении состояния $\ket\psi=\sum_x c_x\ket{x}$ равна

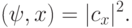$\PP(\ket\psi, x)=|c_x|^2.$

( 8.1)

Нас интересует вероятность того, что компьютер закончит работу в состоянии вида (F(x),z) , где — любое.

Определение 8.1. Схема $U=U_L\cdot\ldots\cdot U_2U_1$ вычисляет , если для любого выполнено

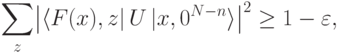
$\sum_{z}^{} \bigl| \langle F(x),z|\,U\,|x,0^{N-n}\rangle\bigr|^2 \ge 1-\varepsilon,$

где $\varepsilon$ — некоторое фиксированное число, меньшее 1/2

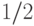. (Обратите внимание, что F(x)

и

состоят из разного количества битов, хотя суммарная длина (F(x),z)

и $(x,0^{N-n})$ одинакова и равна

.)

Как и для вероятностных вычислений, выбор $\varepsilon$ несущественен, поскольку можно запустить несколько экземпляров схемы независимо и выбрать тот результат, который получается чаще всего. Из оценки, приведенной в "Вероятностные алгоритмы и класс BPP. Проверка простоты числа" , следует, что для уменьшения вероятности неудачи в раз нужно взять $O(\log N)$ экземпляров схемы . 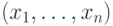Выбор самого частого результата реализуется классической схемой, использующей функцию голосования $\MAJ(x_1,\dots,x_n)$ (она равна 1, когда более половины ее аргументов равны 1, и равна 0 в противном случае). 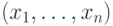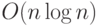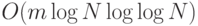Функция $\MAJ(x_1,\dots,x_n)$ реализуется в полном базисе схемой размера $O(n\log n)$ , так что потеря эффективности при уменьшении вероятности неудачи в раз задается множителем $O(m\log N\log\log N)$ .

Задача 8.1. Докажите, что приведенное рассуждение является корректным в квантовом случае: функция $\MAJ_\oplus$ реализована в виде обратимой схемы, на вход которой подаются выходные q-биты копий схемы .

Дальше >>

Авторизоваться

Классические и квантовые вычисления

Определение квантового вычисления. Примеры

Вопросы и ответы