Базисы для квантовых схем
Как выбрать базис для вычислений в квантовых схемах? Унитарных операторов бесконечно много, поэтому либо полный базис должен содержать бесконечное количество элементов, либо мы должны ослабить условие точной реализуемости оператора схемой, заменив его на условие приближенной реализуемости. Мы рассмотрим обе возможности.
Точная реализация.
Теорема 7.1. Базис, содержащий все унитарные операторы, действующие на парах q-битов, позволяет реализовать любой унитарный оператор в расширенном смысле.
Для доказательства этой теоремы введем важный класс операторов: операторы с квантовым управлением.
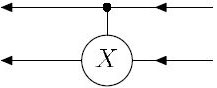
Определение 7.1. Определим по оператору  оператор
оператор 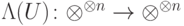 с квантовым управляющим q-битом (первый сомножитель) следующими соотношениями:
с квантовым управляющим q-битом (первый сомножитель) следующими соотношениями:
 |
( 7.1) |
Графически будем изображать оператор  с квантовым управлением как показано на рисунке. Верхняя линия соответствует первому сомножителю, нижняя линия — второму. Направление стрелок соответствует направлению перемножения операторов (справа налево).
с квантовым управлением как показано на рисунке. Верхняя линия соответствует первому сомножителю, нижняя линия — второму. Направление стрелок соответствует направлению перемножения операторов (справа налево).
Нам потребуются также операторы с несколькими управляющими q-битами:
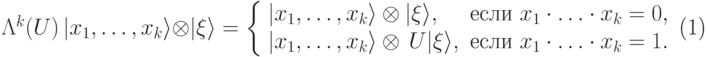 |
( 7.2) |
Пример 7.1. Пусть  . Тогда
. Тогда  , а
, а  (элемент Тоффоли).
(элемент Тоффоли).
Теперь построим элемент Тоффоли, используя преобразования двух q-битов. Для начала найдем пару операторов, удовлетворяющих следующему соотношению 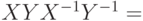 . Например, годится такая пара:
. Например, годится такая пара:
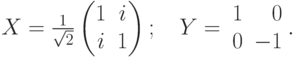
Поясним геометрический смысл этой конструкции. Унитарная группа  действует на трехмерном евклидовом пространстве. Чтобы описать это действие, заметим, что эрмитовы матрицы
действует на трехмерном евклидовом пространстве. Чтобы описать это действие, заметим, что эрмитовы матрицы  с нулевым следом образуют трехмерное евклидово пространство: скалярное произведение задается формулой
с нулевым следом образуют трехмерное евклидово пространство: скалярное произведение задается формулой  , ортонормированный базис образуют матрицы Паули,
, ортонормированный базис образуют матрицы Паули,

 действует на этом пространстве так:
действует на этом пространстве так: 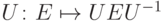 . Можно доказать (см.[8, 11.12]), что описанное действие задает изоморфизм
. Можно доказать (см.[8, 11.12]), что описанное действие задает изоморфизм 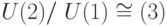 , где
, где 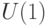 — подгруппа фазовых сдвигов, а
— подгруппа фазовых сдвигов, а  — группа поворотов в трехмерном пространстве (т.е. группа ортогональных преобразований с детерминантом, равным
— группа поворотов в трехмерном пространстве (т.е. группа ортогональных преобразований с детерминантом, равным  ).
).При этом действии  соответствует поворот вокруг оси
соответствует поворот вокруг оси  на
на 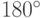 ,
,  соответствует поворот вокруг
соответствует поворот вокруг  на
на  , а
, а  соответствует поворот вокруг
соответствует поворот вокруг 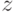 на
на  .
.
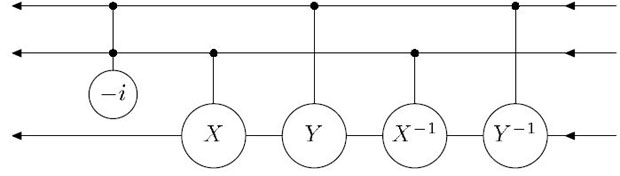
На рис. рис. 7.1 изображено графическое представление схемы, вычисляющей элемент Тоффоли с помощью операторов  ,
, 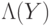 и
и 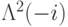 . Последний — это управляемый двумя битами фазовый сдвиг (умножение на
. Последний — это управляемый двумя битами фазовый сдвиг (умножение на 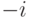 ). Проверим эту схему. Пусть на вход подается вектор
). Проверим эту схему. Пусть на вход подается вектор 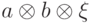 , где
, где 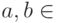 ,
,  . Если
. Если  , то к
, то к 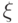 будет применен оператор
будет применен оператор 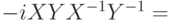 , т.е.
, т.е.  и
и 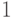 в третьем q-бите переставляются. Если же хотя бы один из управляющих битов равен 0, то к
в третьем q-бите переставляются. Если же хотя бы один из управляющих битов равен 0, то к 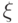 будет применен тождественный оператор. Это и есть действие элемента Тоффоли.
будет применен тождественный оператор. Это и есть действие элемента Тоффоли.
С помощью элемента Тоффоли можно реализовать любую перестановку базисных векторов (с использованием дополнительной памяти).
Покажем, как реализовать оператор 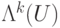 для любого
для любого  , действуя только на пары q-битов. Для этого также потребуется дополнительная память. Будем строить оператор
, действуя только на пары q-битов. Для этого также потребуется дополнительная память. Будем строить оператор 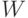 , действующий в пространстве
, действующий в пространстве 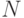 q-битов
q-битов 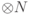 и удовлетворяющий условию
и удовлетворяющий условию
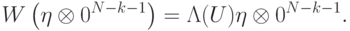
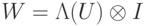 .)
.)Существует обратимая схема  размера
размера  , вычисляющая произведение входных битов (с мусором); графически она представлена на рис. рис. 7.2 (сверху обозначено число битов в каждом из выделенных фрагментов памяти).
, вычисляющая произведение входных битов (с мусором); графически она представлена на рис. рис. 7.2 (сверху обозначено число битов в каждом из выделенных фрагментов памяти).
На рис. 7.3 показано, как с помощью схемы  и оператора с одним управляющим q-битом построить оператор
и оператора с одним управляющим q-битом построить оператор 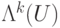 . Мы применяем схему
. Мы применяем схему  , а затем — обратную схему
, а затем — обратную схему 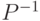 , после чего все вспомогательные биты возвращаются в исходное состояние. В промежутке самой верхней линии соответствует бит со значением
, после чего все вспомогательные биты возвращаются в исходное состояние. В промежутке самой верхней линии соответствует бит со значением 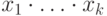 . Его мы и используем для управления оператором
. Его мы и используем для управления оператором 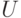 , действующим на самой нижней линии. Другим способом
, действующим на самой нижней линии. Другим способом 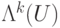 можно записать как
можно записать как 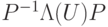 .
.
Действие 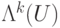 можно описать так: на подпространстве, порожденном векторами
можно описать так: на подпространстве, порожденном векторами 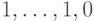 и
и 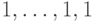 , действует оператор
, действует оператор 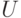 , а на ортогональном дополнении к этому подпространству — тождественный оператор. Наша следующая задача: реализовать оператор, который устроен так же, но нетривиальное действие осуществляется на подпространстве, натянутом на произвольную пару базисных векторов. Пусть мы хотим реализовать произвольный оператор в подпространстве, натянутом на базисные векторы
, а на ортогональном дополнении к этому подпространству — тождественный оператор. Наша следующая задача: реализовать оператор, который устроен так же, но нетривиальное действие осуществляется на подпространстве, натянутом на произвольную пару базисных векторов. Пусть мы хотим реализовать произвольный оператор в подпространстве, натянутом на базисные векторы 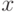 и
и 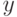 , где
, где 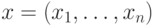 ,
, 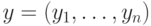 ,
, 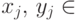 . Пусть
. Пусть  — такая перестановка, что
— такая перестановка, что 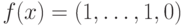 ,
,  . Тогда нужный нам оператор представляется в виде
. Тогда нужный нам оператор представляется в виде  . (Напомним, что
. (Напомним, что 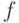 — оператор, соответствующий перестановке
— оператор, соответствующий перестановке  .)
.)
Итак, на парах базисных векторов мы можем действовать произвольно. Пока все использованные схемы имели размер  , так что построенные действия реализуются эффективно. Следующая часть неэффективна. Имеет место следующая лемма.
, так что построенные действия реализуются эффективно. Следующая часть неэффективна. Имеет место следующая лемма.
Лемма 7.1. Любая унитарная матрица 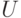 в пространстве
в пространстве 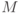 может быть представлена в виде произведения
может быть представлена в виде произведения 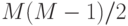 матриц вида
матриц вида
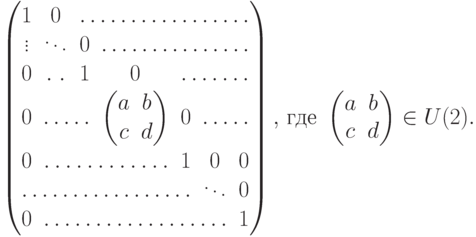
Заметим, что в нашем случае  , так что получаем представление в виде произведения экспоненциального большого числа базисных операторов.
, так что получаем представление в виде произведения экспоненциального большого числа базисных операторов.