Квантовый аналог NP: класс BQNP
Можно строить квантовые аналоги не только для класса P, но и для других классических сложностных классов. Мы разберем пример квантового аналога класса NP.
Модификация классических определений
Квантовое вычисление, как, впрочем, и вероятностное, наиболее естественно описывать, используя частично определенные функции. Ранее мы обходились без этого понятия, чтобы не усложнять изложение лишними деталями, но теперь оно нам потребуется.
Частично определенная булева функция — это функция

И еще одно замечание по поводу обозначений: мы использовали обозначение P и для класса полиномиально вычислимых функций, и для класса полиномиально разрешимых предикатов; теперь поступим аналогично, используя обозначения P, NP и т.п. для классов частично определенных функций.
P, естественно, обозначает класс полиномиально вычислимых частично определенных функций. Приведем модифицированное определение класса NP.
Определение 13.1. Функция  принадлежит классу NP, если есть частично определенная функция
принадлежит классу NP, если есть частично определенная функция  от двух переменных, такая что
от двух переменных, такая что
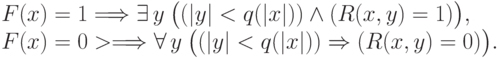
 — полином.
— полином.Что будет, если в определении 13.1 заменить условие  на условие
на условие 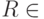 ? Получится другой, скорее всего, более широкий класс, который можно было бы обозначить BNP. Однако для этого класса есть другое, стандартное, обозначение — MA, указывающее на то, что он входит в иерархию классов, определяемых играми Артура - Мерлина. Об играх, которыми задаются сложностные классы, мы уже говорили в
"Иерархия сложностных классов"
; игры Артура - Мерлина отличаются тем, что Артур — вероятностная полиномиальная машина Тьюринга. Порядок букв в обозначении MA указывает на порядок ходов: вначале Мерлин сообщает
? Получится другой, скорее всего, более широкий класс, который можно было бы обозначить BNP. Однако для этого класса есть другое, стандартное, обозначение — MA, указывающее на то, что он входит в иерархию классов, определяемых играми Артура - Мерлина. Об играх, которыми задаются сложностные классы, мы уже говорили в
"Иерархия сложностных классов"
; игры Артура - Мерлина отличаются тем, что Артур — вероятностная полиномиальная машина Тьюринга. Порядок букв в обозначении MA указывает на порядок ходов: вначале Мерлин сообщает  , затем Артур проверяет выполнение предиката
, затем Артур проверяет выполнение предиката 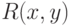 .
.
Квантовое определение по аналогии.
Определение 13.2. Функция 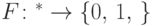 принадлежит классу
принадлежит классу  , если существует однородная последовательность квантовых схем полиномиального по
, если существует однородная последовательность квантовых схем полиномиального по  размера, реализующих такие операторы
размера, реализующих такие операторы  , что
, что
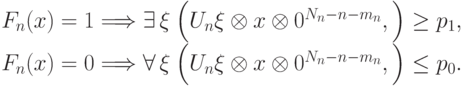
Здесь 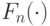 — ограничение
— ограничение  на слова длины
на слова длины  ,
,  ,
,  ,
,  , а для
, а для  и
и 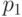 должно выполняться условие
должно выполняться условие  ,
,  .
.
Вектор 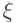 выполняет роль подсказки (
выполняет роль подсказки (  ) из предыдущего определения. Нам удобнее считать его первым аргументом оператора
) из предыдущего определения. Нам удобнее считать его первым аргументом оператора 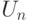 (чтобы можно было в любой момент положить
(чтобы можно было в любой момент положить  константой и исключить из обозначений).
константой и исключить из обозначений).
Замечание 13.1. В определении кванторы по 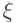 включают в себя только векторы единичной длины. Аналогичное соглашение будем использовать и далее в этом разделе, вынося нормировочные множители за знак
включают в себя только векторы единичной длины. Аналогичное соглашение будем использовать и далее в этом разделе, вынося нормировочные множители за знак  .
.
Если вместо чистых состояний 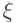 рассматривать смешанные, то получается эквивалентное определение: максимум вероятности все равно достигается на чистом состоянии.
рассматривать смешанные, то получается эквивалентное определение: максимум вероятности все равно достигается на чистом состоянии.
По сути происходит все та же игра Мерлина с Артуром, только теперь подчиняющаяся законам квантовой механики. Сообщение Мерлина (состояние 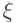 ) дает Артуру возможность убедиться в том, что
) дает Артуру возможность убедиться в том, что  с вероятностью
с вероятностью 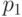 , если это так. А если
, если это так. А если 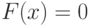 , то вероятность, что Мерлину удастся убедить Артура в обратном, не выше
, то вероятность, что Мерлину удастся убедить Артура в обратном, не выше  для любого сообщения Мерлина.
для любого сообщения Мерлина.
Обсудим теперь соотношения между пороговыми вероятностями. Из приведенного в определении 13.2 соотношения следует гораздо более сильное условие на  и
и 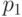 .
.
