НОУ ИНТУИТ | Классические и квантовые вычисления. Лекция 13: Квантовый аналог NP: класс BQNP

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Московский государственный университет имени М.В.Ломоносова

Опубликован: 15.03.2007 | Доступ: свободный | Студентов: 617 / 28 | Оценка: 5.00 / 4.50 | Длительность: 19:30:00

Тема: Алгоритмы и дискретные структуры

Специальности: Программист

|

Вам нравится? Нравится 11 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

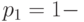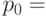Лемма 13.1 (усиление вероятностей). Если $F\in\BQNP$ , то она удовлетворяет также и такому варианту определения 13.2, где условие $p_1-p_0=\Omega(n^{-\alpha})$ заменено на $p_1=1-\eps$ , $p_0=\eps$ , $\eps=\exp(-O(n^\beta))$ , $\beta>0$ .

Доказательство. Общая идея усиления вероятностей остается прежней: рассмотрим большое, но ограниченное полиномом, количество копий схемы, реализующей оператор 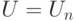U=U_n (индекс мы будем опускать). К результатам их работы применим функцию голосования с пороговым значением, разделяющим вероятности p_0 и p_1 :

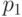$\begin{equation}\label{пороговая-функция} G(z_1,\dots,z_k) = \left\{\begin{array}{ll} 1, & \text{если}\ \sum\limits_{j=1}^{k} z_j \ge l \\[3pt] 0, & \text{если}\ \sum\limits_{j=1}^{k} z_j < l, \end{array}\right. \end{equation}$

( 13.1)

где

,

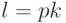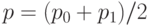. Но теперь появляется дополнительная трудность — Мерлин может пытаться обмануть Артура, сообщая ему неразложимую в тензорное произведение подсказку.

Пусть мы используем копий схемы . Предоставим Мерлину большую свободу, разрешив в качестве подсказки любую матрицу плотности $\rho\in\LL(\BB^{\otimes km})$ . Вероятность получения ответов $z_1,\dots,z_k$ при подсказке $\rho$ равна

$\begin{equation}\label{вер-послед} \PP(z_1,\dots,z_k|\,\rho)= \Tr(X^{(z_1)}\otimes\ldots\otimes X^{(z_k)}\rho), \end{equation}$

( 13.2)

где

$\begin{equation}\label{принимающий-оператор} X^{(a)}=\Tr_{[m+1,\dots,N]}\Bigl(U^\dagger\Pi^{(a)}_1 U \bigl(I_{\BB^{\otimes m}}\otimes\ket{x,0^{N-n-m}}\bra{x,0^{N-n-m}}\bigr)\Bigr). \end{equation}$

( 13.3)

Здесь 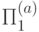$\Pi^{(a)}_1$ — проектор на подпространство состояний, имеющих в первом q-бите (т.е. $\CC(\ket{a})\otimes\BB^{\otimes (N-1)}$ ).

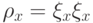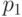Чтобы убедить Артура в правильности F(x)=1 , Мерлин может дать подсказку $\rho=\rho_x^{\otimes k}$ , где $\rho_x=\ket{\xi_x}\bra{\xi_x}$ — сообщение, которое убеждает Артура, действующего по схеме , с вероятностью p_1 . По общим свойствам квантовой вероятности, формула (13.2) преобразуется в

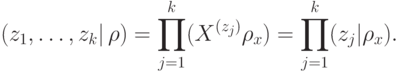
$\PP(z_1,\dots,z_k|\,\rho)=\prod_{j=1}^{k} \Tr(X^{(z_j)}\rho_x) =\prod_{j=1}^{k} \PP(z_j|\rho_x).$

Рассмотрим теперь случай, когда 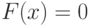F(x)=0 . Нам нужно оценить вероятность $\PP(z_1,\dots, z_k)$ для произвольного сообщения Мерлина $\rho$ . Выберем в пространстве $\BB^{\otimes m}$ ортонормированный базис, в котором диагонализуется оператор $X^{(1)}$ (этот оператор, очевидно, эрмитов). Оператор $X^{(0)}=I-X^{(1)}$ диагонален в том же базисе. 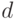Определим набор "условных вероятностей" $p(z|d)=\bra{d}X^{(z)}\ket{d}$ , где $\ket{d}$ — один из базисных векторов. (Очевидно, что $p(z|d)\ge 0$ и p(0|d)+p(1|d)=1 .) Тогда величина $\PP(z_1,\dots,z_k|\,\rho)$ приобретает вид

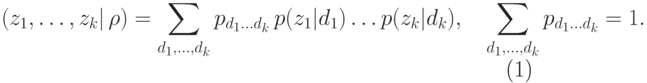$\begin{equation}\label{разл-вер-на подсказке} \PP(z_1,\dots,z_k|\,\rho)= \sum_{d_1,\dots,d_k}p_{d_1\dots d_k}\,p(z_1|d_1)\dots p(z_k|d_k), \quad \sum_{d_1,\dots,d_k}p_{d_1\dots d_k}=1. \end{equation}$

( 13.4)

Здесь $p_{d_1\dots d_k}=\bra{d_1\dots d_k}\rho\ket{d_1\dots d_k}$ .

Формула (13.4) имеет следующую интерпретацию. Рассмотрим набор вероятностей $\PP(z_1,\dots,z_k|\,\rho)$ для всех последовательностей $(z_1,\double\dots,z_k)$ как вектор в -мерном вещественном пространстве. Мы показали, что этот вектор на произвольной подсказке $\rho$ принадлежит выпуклой оболочке таких же векторов на разложимых подсказках $\ket{d_1,\dots,d_n}$ . Поэтому наибольшая вероятность события $G(z_1,\dots,z_k)=1$ (для любой функции ) достигается на подсказках такого вида.

В случае, когда — пороговая функция (13.1),

$\begin{equation}\label{наибольшая-вероятность-принятия} p_{\rm max}= \max_{\rho}\Prob\left[G(z_1,\dots,z_k)=1\big|\,\rho\right]= \sum_{j\ge l} \binom{k}{j} p_*^j(1-p_*)^{k-j}, \end{equation}$

( 13.5)

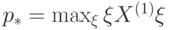где $p_*=\max_{\ket{\xi}}\bra{\xi}X^{(1)}\ket{\xi}$ . Согласно условию, $p_*\ge p_1$ , если F(x)=1

, и $p_*\le p_0$ , если F(x)=0

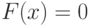. Оценим величину $p_{\rm max}$ в этих случаях, соответственно, снизу и сверху.

Будем использовать неравенство Чернова (см. [18]). Пусть

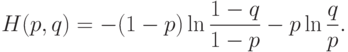
$H(p,q)=-(1-p)\ln\frac{1-q}{1-p}-p\ln\frac{q}{p}.$

Тогда при $p_*\ge p_1$ получаем

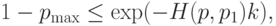
$1-p_{\rm max}\le\exp(-H(p,p_1)k),$

а при $p_*\le p_0$ —

$p_{\rm max}\le\exp(-H(p,p_0)k).$

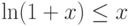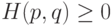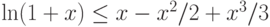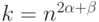Из неравенства $\ln(1+x)\le x$ следует, что $H(p,q)\ge 0$ . Используя более точное разложение $\ln(1+x)\le x-x^2/2+x^3/3$ , можно получить оценку $H(p,q)=\Omega((p-q)^2)$ . Так что при $k=n^{2\alpha+\beta}$ указанные в условии оценки на 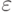$\eps$ выполнены.

Замечание 13.2. Важным моментом в изложенном доказательстве является тот факт, что $X^{(0)}$ и $X^{(1)}$ диагонализуются в одном и том же базисе. Вообще, усиление вероятностей для нетривиальных сложностных классов (как квантовых, так и классических) — вещь довольно тонкая.

Дальше >>

Авторизоваться

Классические и квантовые вычисления

Квантовый аналог NP: класс BQNP

Вопросы и ответы