Квантовый аналог NP: класс BQNP
Полные задачи.
В классе BQNP, как и в NP, есть полные задачи относительно той же самой полиномиальной сводимости, которую мы рассматривали раньше. Вот простейший пример.
Задача 0. Зададим функцию  следующим образом. Пусть
следующим образом. Пусть  — множество троек вида
— множество троек вида

 (
( 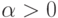 ,
,  — размер описания схемы). Тогда для
— размер описания схемы). Тогда для 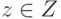
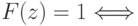 если существует вектор
если существует вектор 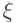 , при действии на который мы получим в первом бите 1 с вероятностью, большей
, при действии на который мы получим в первом бите 1 с вероятностью, большей 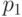 ;
;
 если для всех
если для всех 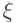 вероятность получить в первом бите 1 меньше
вероятность получить в первом бите 1 меньше  .
.
Полнота задачи 0 очевидна. Все, что требуется для построения сведения, содержится в определении 13.2. Вход  войдет в описание схемы
войдет в описание схемы  вместе со схемой
вместе со схемой 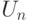 .
.
Рассмотрим более интересные примеры. Для начала дадим определение квантового аналога 3-КНФ — локального гамильтониана (локальность является аналогом ограниченности числа переменных, входящих в одну дизъюнкцию).
Определение 13.3. Оператор  называется k-локальным гамильтонианом, если он выражается в виде
называется k-локальным гамильтонианом, если он выражается в виде
![H=\sum_{j}^{} H_j[S_j],](/sites/default/files/tex_cache/b36059beeee11344e2fe0fced00e672e.png)
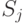 ,
,  , на остальных q-битах он действует тождественно.
, на остальных q-битах он действует тождественно.При этом выполнено условие нормировки 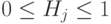 (другими словами, и
(другими словами, и 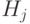 , и
, и 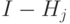 — положительно полуопределенные).
— положительно полуопределенные).
Задача 1: локальный гамильтониан. Пусть  — множество троек вида
— множество троек вида
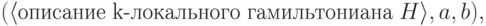
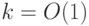 ,
, 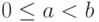 ,
, 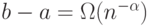 , (
, ( 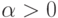 ). Тогда для
). Тогда для 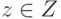
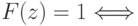 если у
если у  есть собственное число, не большее
есть собственное число, не большее  ,
,
 если все собственные числа
если все собственные числа  больше
больше  .
.
Утверждение 13.2. Задача локальный гамильтониан принадлежит BQNP.
Доказательство. Опишем вначале основную идею. Мы построим такую схему  , которая использует подсказку из пространства, в котором действует
, которая использует подсказку из пространства, в котором действует  , и выдает ответ "да" (значение 1) на подсказке
, и выдает ответ "да" (значение 1) на подсказке 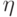 с вероятностью
с вероятностью  , где
, где  — число слагаемых в гамильтониане
— число слагаемых в гамильтониане  . Если
. Если 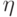 — собственный вектор, соответствующий собственному числу
— собственный вектор, соответствующий собственному числу  , то вероятность ответа "да" будет
, то вероятность ответа "да" будет
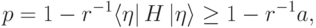
 больше
больше  , то
, то
Сперва построим такую схему для одного слагаемого. Пусть это будет  , действующий на множестве q-битов
, действующий на множестве q-битов 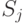 . Поскольку размерность пространства, на котором действует
. Поскольку размерность пространства, на котором действует 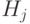 , ограничена константой, мы можем реализовать оператор
, ограничена константой, мы можем реализовать оператор

 , где
, где  обозначает q-бит, из которого берется результат работы схемы. На остальных q-битах подсказки
обозначает q-бит, из которого берется результат работы схемы. На остальных q-битах подсказки 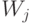 действует тождественно.
действует тождественно.Вычислим вероятность 1 в бите результата после применения 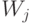 к состоянию
к состоянию 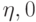 (бит результата установлен в 0 перед началом работы схемы). Пусть
(бит результата установлен в 0 перед началом работы схемы). Пусть  — разложение
— разложение 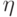 по ортогональной системе собственных векторов
по ортогональной системе собственных векторов 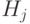 . Имеем, по определению вероятности,
. Имеем, по определению вероятности,
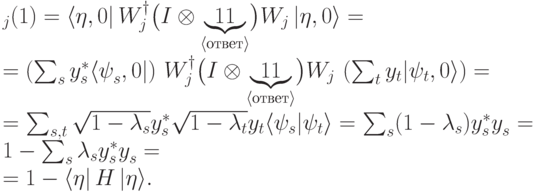 |
( 13.6) |
Общая схема  выбирает случайно и равновероятно номер
выбирает случайно и равновероятно номер  , после чего применяет оператор
, после чего применяет оператор 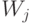 . Такое действие можно реализовать измеряющим оператором вида
. Такое действие можно реализовать измеряющим оператором вида 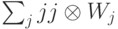 , примененным к вектору
, примененным к вектору
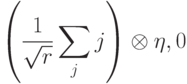
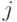 обозначает базисный вектор во вспомогательном
обозначает базисный вектор во вспомогательном  -мерном пространстве.) Проводя вычисления аналогично (13.6), получаем
-мерном пространстве.) Проводя вычисления аналогично (13.6), получаем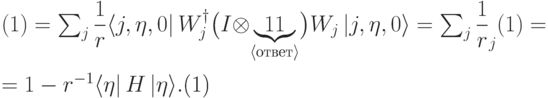 |
( 13.7) |
