Вероятностные алгоритмы и класс BPP. Проверка простоты числа
В вероятностных МТ (ВМТ), как и в недетерминированных, имеются состояния, из которых возможен переход в несколько (больше одного) состояний. Отличие состоит в том, что состояние, куда ВМТ делает переход, определяется результатом некоторого случайного процесса ("подбрасывания монеты"). Нужно оговорить, какие монеты допускаются. Например, если взять монету, вероятность выпадения герба для которой равна невычислимому числу, то возможности ВМТ, использующей подбрасывание такой монеты, будут больше, чем хотелось бы; она сможет вычислить и некоторые неразрешимые предикаты.
Обычно считают, что вероятности выпадения одинаковы для обеих сторон монеты, а результат подбрасывания отождествляется с числом 0 или 1.
Хотя для ВМТ нельзя сказать, какой в точности ответ она выдаст, можно определить вероятность того или иного ответа.
Определение 3.1. Предикат  принадлежит классу BPP, если существуют такие ВМТ
принадлежит классу BPP, если существуют такие ВМТ  и полином
и полином 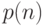 , что машина
, что машина  заведомо остановится за время, не превосходящее
заведомо остановится за время, не превосходящее 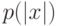 , причем
, причем


 с вероятностью большей
с вероятностью большей  дает ответ "да";
дает ответ "да";
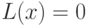

 с вероятностью большей
с вероятностью большей  дает ответ "нет".
дает ответ "нет".
Если в этом определении заменить число  на любое фиксированное число, большее
на любое фиксированное число, большее 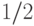 , класс BPP не изменится. Есть простой способ добиться вероятности, сколь угодно близкой к 1. Возьмем несколько одинаковых машин, запустим их все, а окончательным результатом будем считать мнение большинства. Если вероятность правильного ответа для каждого экземпляра машины равна
, класс BPP не изменится. Есть простой способ добиться вероятности, сколь угодно близкой к 1. Возьмем несколько одинаковых машин, запустим их все, а окончательным результатом будем считать мнение большинства. Если вероятность правильного ответа для каждого экземпляра машины равна 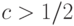 , то можно доказать, что
вероятность правильного ответа после голосования
, то можно доказать, что
вероятность правильного ответа после голосования  машин не меньше
машин не меньше  , где
, где 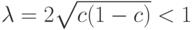 .
.
Замечание 3.1. Представить физическую реализацию НМТ очень трудно (вспомним, что нам придется поместить в нее всезнайку Мерлина). А вероятностные машины вполне могут мыслиться как реальные устройства. Поэтому предикаты из класса BPP вполне можно считать реально вычислимыми.
Класс BPP можно определить и с помощью предикатов от двух переменных, как это было сделано для класса NP.
Определение 3.2. Предикат  принадлежит классу BPP, если существуют такие полином
принадлежит классу BPP, если существуют такие полином  и предикат
и предикат 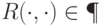 , что
, что

 доля слов
доля слов  длины
длины 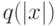 , для которых выполнено
, для которых выполнено 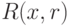 , больше
, больше  ;
;
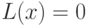
 доля слов
доля слов  длины
длины 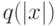 , для которых выполнено
, для которых выполнено 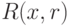 , меньше
, меньше 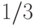 .
.
Теорема 3.1. Определения 3.1 и 3.2 эквивалентны.
Доказательство Опр. 3.1  Полагаем
Полагаем  (количество подбрасываний монеты не превосходит общего числа действий). Определим предикат
(количество подбрасываний монеты не превосходит общего числа действий). Определим предикат 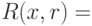 "машина
"машина  на входе
на входе  дает ответ "да" при указанной в
дает ответ "да" при указанной в  последовательности результатов подбрасываний монеты". Этот предикат по очевидным причинам удовлетворяет определению 3.2.
последовательности результатов подбрасываний монеты". Этот предикат по очевидным причинам удовлетворяет определению 3.2.
Опр. 3.2  опр. 3.1. Случайно выбираем слово
опр. 3.1. Случайно выбираем слово  длины
длины 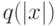 и подставляем в предикат, затем вычисляем значение предиката. Такая ВМТ удовлетворяет определению 3.1.
и подставляем в предикат, затем вычисляем значение предиката. Такая ВМТ удовлетворяет определению 3.1.
Определение 3.2 допускает следующее наглядное толкование. Отметим на плоскости  точки из множества
точки из множества  . Для
. Для  рассмотрим сечение
рассмотрим сечение  этого множества. Предикат
этого множества. Предикат 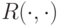 , участвующий в определении 3.2, обладает таким странным свойством, что мера этого сечения при любом
, участвующий в определении 3.2, обладает таким странным свойством, что мера этого сечения при любом  либо больше
либо больше  , либо меньше
, либо меньше 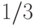 . Это разделяет значения
. Это разделяет значения  на две категории: одна соответствует истинности предиката
на две категории: одна соответствует истинности предиката  , другая — ложности.
, другая — ложности.
Классический пример задачи из BPP представляет проверка простоты числа: дано число  , требуется определить, простое ли оно. Для этой задачи существует вероятностный алгоритм, работающий за
полиномиальное время; он будет сейчас описан.
, требуется определить, простое ли оно. Для этой задачи существует вероятностный алгоритм, работающий за
полиномиальное время; он будет сейчас описан.
Необходимые сведения из теории чисел.
Подробное изложение элементарной теории чисел содержится в книге [2]. Мы лишь напомним две теоремы, которые будут важны при анализе работы алгоритма проверки простоты числа.
Малая теорема Ферма. Если  — простое и
— простое и 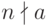 , то
, то  .
.
Китайская теорема об остатках. Пусть 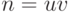 — разложение числа на взаимно простые множители. Тогда
— разложение числа на взаимно простые множители. Тогда 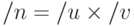 .
.
Другими словами, существует взаимно однозначное соответствие между остатками от деления на  и парами остатков от деления на
и парами остатков от деления на  и на
и на  . {И это соответствие уважает операции сложения и умножения.)
. {И это соответствие уважает операции сложения и умножения.)
Из малой теоремы Ферма следует, что  позволяет утверждать, что
позволяет утверждать, что  — составное (говорят, что
— составное (говорят, что  является свидетелем непростоты числа
является свидетелем непростоты числа  ). Это свидетельство косвенное — явного разложения
). Это свидетельство косвенное — явного разложения  на множители мы не получаем — и сильное: часто достаточно проверки при
на множители мы не получаем — и сильное: часто достаточно проверки при  !
!
Однако проверки малой теоремы Ферма даже при всех  может оказаться недостаточно. Алгоритм проверки будет использовать свидетелей еще одного типа: если
может оказаться недостаточно. Алгоритм проверки будет использовать свидетелей еще одного типа: если  , а
, а 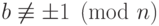 , то
, то  — составное;
— составное;  и
и  имеют общий делитель, больший 1. Поэтому свидетели такого вида (вообще говоря, гораздо более редко появляющиеся) позволяют сразу же указать разложение
имеют общий делитель, больший 1. Поэтому свидетели такого вида (вообще говоря, гораздо более редко появляющиеся) позволяют сразу же указать разложение  (против простоты которого они свидетельствуют) на два множителя за полиномиальное время (наибольший общий делитель
(против простоты которого они свидетельствуют) на два множителя за полиномиальное время (наибольший общий делитель  двух чисел
двух чисел  и
и  можно найти за полиномиальное время, см. ниже).
можно найти за полиномиальное время, см. ниже).
Необходимые сведения из алгоритмической теории чисел.
Арифметические операции над числами можно выполнять за полиномиальное время от длины их записи (число  записывается
записывается  знаками). Например, схема умножения чисел
знаками). Например, схема умножения чисел  ,
,  столбиком имеет размер
столбиком имеет размер 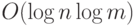 , растущий квадратично от длины входа. Хотя квадрат от длины входа уже достаточно мал, чтобы быть полиномиальным, заметим, что для умножения
, растущий квадратично от длины входа. Хотя квадрат от длины входа уже достаточно мал, чтобы быть полиномиальным, заметим, что для умножения  -значных чисел есть и более экономные схемы размера
-значных чисел есть и более экономные схемы размера 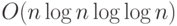 , см.[
"Что такое алгоритм?"
] или [7, т. 2, р.4.3.3].
, см.[
"Что такое алгоритм?"
] или [7, т. 2, р.4.3.3].
В модулярной арифметике (арифметике остатков по модулю заданного числа  ) можно вычислить
) можно вычислить 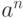 по модулю
по модулю  схемой полиномиального размера от длины входа
схемой полиномиального размера от длины входа 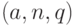 (в обычной арифметике даже результат возведения в степень может иметь экспоненциальный размер). Для этого нужно вычислить остатки от степеней
(в обычной арифметике даже результат возведения в степень может иметь экспоненциальный размер). Для этого нужно вычислить остатки от степеней  последовательным возведением в квадрат и затем перемножить те из полученных чисел, которым соответствуют 1 в двоичной записи числа
последовательным возведением в квадрат и затем перемножить те из полученных чисел, которым соответствуют 1 в двоичной записи числа  .
.
Наибольший общий делитель двух чисел можно найти, пользуясь алгоритмом Евклида, использующим рекурсивно равенство 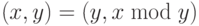 . Если делить большее число на меньшее, то за каждые два шага длина записи меньшего числа уменьшается на константу.
. Если делить большее число на меньшее, то за каждые два шага длина записи меньшего числа уменьшается на константу.
Существует также алгоритм проверки того, что из числа извлекается нацело корень  -й степени. Это можно сделать, найдя достаточно точно приближенное значение корня и возведя ближайшее к нему целое число в
-й степени. Это можно сделать, найдя достаточно точно приближенное значение корня и возведя ближайшее к нему целое число в  -ю степень. Найти приближенное значение
-ю степень. Найти приближенное значение ![\sqrt[k\mkern3mu]{x}](/sites/default/files/tex_cache/f290138b7cc2c7271844a66d6c7b0e6b.png) можно с помощью рекуррентной последовательности
можно с помощью рекуррентной последовательности

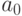 . Детали этого (полиномиального) алгоритма оставляются читателю для самостоятельного обдумывания.
. Детали этого (полиномиального) алгоритма оставляются читателю для самостоятельного обдумывания.Заметим, что все схемы, о которых шла речь выше, могут быть построены МТ за полиномиальное время. Так что все перечисленные задачи принадлежат классу P.

