Решения задач
1.19 а)  б). Граф, представляющий формулу, можно сделать деревом, если размножить входные переменные. Размер при этом увеличится не более, чем вдвое.
б). Граф, представляющий формулу, можно сделать деревом, если размножить входные переменные. Размер при этом увеличится не более, чем вдвое.
Для построения схемы глубины  , вычисляющей формулу
, вычисляющей формулу  размера
размера  , используем идею, примененную в решении задач 1.14 и 1.15.
, используем идею, примененную в решении задач 1.14 и 1.15.
Двигаясь от корня дерева, представляющего формулу, и выбирая каждый раз вершину, соответствующую подформуле большего размера, мы найдем рано или поздно подформулу  , размер которой лежит между
, размер которой лежит между 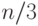 и
и 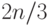 . Заменяя в формуле
. Заменяя в формуле  подформулу
подформулу  независимой переменной
независимой переменной  , получаем формулу
, получаем формулу  с такими же оценками на размер.
с такими же оценками на размер.
Пусть для  и
и  есть вычисляющие их схемы глубины не больше
есть вычисляющие их схемы глубины не больше  . Построим для всей формулы
. Построим для всей формулы  схему глубины не больше
схему глубины не больше  . Вычислим 3 переменные подсхемами глубины не больше
. Вычислим 3 переменные подсхемами глубины не больше  :
: 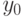 — значение формулы
— значение формулы  при
при 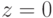 ,
, 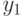 — значение формулы
— значение формулы  при
при 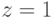 ,
,  — значение формулы
— значение формулы  . Значение
. Значение  всей формулы равно
всей формулы равно

Итак, для 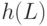 — минимальной глубины схемы, вычисляющей формулу размера
— минимальной глубины схемы, вычисляющей формулу размера  , выполнено рекуррентное соотношение:
, выполнено рекуррентное соотношение:

 .
.б)  а). Это совсем просто. Превратим граф схемы в дерево, размножая при необходимости вершины. Размер этого дерева не будет превышать количества ориентированных путей от выхода ко входам. А таких путей не более
а). Это совсем просто. Превратим граф схемы в дерево, размножая при необходимости вершины. Размер этого дерева не будет превышать количества ориентированных путей от выхода ко входам. А таких путей не более  .
.
1.20 Вспомним конструкцию неразрешимого предиката 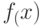 , принадлежащего P/poly, которая приведена в замечании 1.1.
, принадлежащего P/poly, которая приведена в замечании 1.1.
Сейчас мы будем строить такой предикат 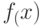 , чтобы он был разрешим, но не принадлежал P. Мы построим такую вычислимую функцию
, чтобы он был разрешим, но не принадлежал P. Мы построим такую вычислимую функцию  , что любой алгоритм ее вычисления работает дольше, чем
, что любой алгоритм ее вычисления работает дольше, чем  . Другими словами, есть алгоритм распознавания принадлежности языку
. Другими словами, есть алгоритм распознавания принадлежности языку  , состоящему из двоичных записей тех чисел
, состоящему из двоичных записей тех чисел  , для которых
, для которых 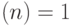 ; но время работы в наихудшем случае любого такого алгоритма на словах длины
; но время работы в наихудшем случае любого такого алгоритма на словах длины  растет быстрее, чем
растет быстрее, чем 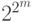 .
.
Докажем более общее утверждение. Пусть 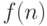 — вычислимая функция. Обозначим через
— вычислимая функция. Обозначим через 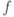 язык, состоящий из таких пар
язык, состоящий из таких пар ![([M],x)](/sites/default/files/tex_cache/fb63afa84f2a2290c3a9a384c64f1476.png) , что машина
, что машина  на входе
на входе  останавливается за время
останавливается за время 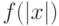 . Принадлежность этому языку разрешима (запустим универсальную машину Тьюринга со входом
. Принадлежность этому языку разрешима (запустим универсальную машину Тьюринга со входом ![([M],x)](/sites/default/files/tex_cache/fb63afa84f2a2290c3a9a384c64f1476.png) , отсчитаем
, отсчитаем 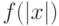 тактов работы
тактов работы  и посмотрим — остановилась ли
и посмотрим — остановилась ли  ). Но быстро проверить эту разрешимость нельзя, как показывает следующее рассуждение, почти дословно повторяющее решение задачи 1.3.
). Но быстро проверить эту разрешимость нельзя, как показывает следующее рассуждение, почти дословно повторяющее решение задачи 1.3.
Пусть машина  распознает принадлежность языку
распознает принадлежность языку 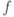 слов длины
слов длины  за время
за время 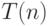 . Тогда есть и такая машина
. Тогда есть и такая машина 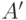 , которая на входе
, которая на входе  запускает
запускает  на входе
на входе  , после чего в случае ответа "да" переходит в состояние, в котором головка двигается вправо (и машина не останавливается), а в случае ответа "нет" останавливается. Смоделировать работу
, после чего в случае ответа "да" переходит в состояние, в котором головка двигается вправо (и машина не останавливается), а в случае ответа "нет" останавливается. Смоделировать работу  за время
за время 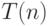 можно за время
можно за время 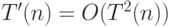 . Если
. Если 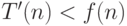 , то что скажет
, то что скажет  о слове
о слове ![([A'],[A'])](/sites/default/files/tex_cache/b84517d11178749b0e9c6600633da900.png) ? Если "да", то приходим к противоречию с определением машины
? Если "да", то приходим к противоречию с определением машины 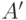 , если "нет" — тоже приходим к противоречию. Поэтому
, если "нет" — тоже приходим к противоречию. Поэтому 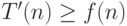 , а
, а 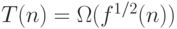 .
.
Итак, мы доказали, что время работы любого алгоритма, распознающего принадлежность слова языку 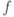 не меньше, чем
не меньше, чем 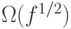 .
.
Взяв в качестве  функцию
функцию 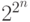 , получим решение задачи.
, получим решение задачи.
Из раздела 2
2.1 Напомним, что литералом называется переменная или ее отрицание. Литералы будем обозначать 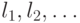 . Алгоритм решения задачи 2-КНФ будет работать в три этапа.
. Алгоритм решения задачи 2-КНФ будет работать в три этапа.
Этап 1. Перебираем все пары дизъюнкций. Если встречаем пару  ,
, 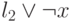 , то добавляем к КНФ дизъюнкцию
, то добавляем к КНФ дизъюнкцию  . Если все пары (включая добавленные дизъюнкции) просмотрены, то переходим к этапу 2.
. Если все пары (включая добавленные дизъюнкции) просмотрены, то переходим к этапу 2.
Этап 2. Проверяем для каждой пары переменных, сколько дизъюнкций использует эту пару. Если каждая пара используется не более одного раза, то выдаем ответ "да" (КНФ выполнима). Если нашлась пара переменных, используемая по крайней мере в двух дизъюнкциях, выполняем сокращение: делаем подстановку равенств, указанных в третьей строчке следующей таблицы, во все дизъюнкции и если получаем противоречие ( 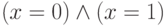 или
или 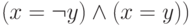 , то выдаем ответ "нет", в противном случае переходим к этапу 3.
, то выдаем ответ "нет", в противном случае переходим к этапу 3.
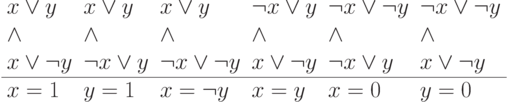
Этап 3. Решаем полученную на этапе 2 задачу с меньшим числом переменных и повторяем ее ответ.
Корректность такого алгоритма вытекает из следующих наблюдений. Во-первых, в силу логического тождества
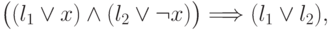
Наконец, докажем, что если на каждой паре переменных есть не более одной дизъюнкции, то КНФ, полученная ко второму этапу, выполнима. Присвоим значение переменной  произвольным образом, затем учтем все следствия этого присвоения. Первой из переменных, которой не присвоено значение, также присвоим значение произвольным образом и т.д. Когда мы не получим выполняющего набора значений переменных? Только в том случае, если для некоторой переменной из значений ранее определенных переменных будут следовать и 0, и 1. Рассмотрим самое раннее такое противоречие. Оно означает, что имеются дизъюнкции
произвольным образом, затем учтем все следствия этого присвоения. Первой из переменных, которой не присвоено значение, также присвоим значение произвольным образом и т.д. Когда мы не получим выполняющего набора значений переменных? Только в том случае, если для некоторой переменной из значений ранее определенных переменных будут следовать и 0, и 1. Рассмотрим самое раннее такое противоречие. Оно означает, что имеются дизъюнкции  и
и 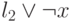 , а также, что
, а также, что 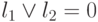 . Но это невозможно, так как в этом случае дизъюнкция
. Но это невозможно, так как в этом случае дизъюнкция  также входит в КНФ после этапа 1.
также входит в КНФ после этапа 1.
Теперь оценим время работы алгоритма в худшем случае. Обозначим его через 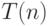 , где
, где  — число переменных (число переменных заведомо не превосходит длины входа). По построению имеем следующее рекуррентное соотношение
— число переменных (число переменных заведомо не превосходит длины входа). По построению имеем следующее рекуррентное соотношение

 .
.2.2 Степенью вершины в графе называется количество ребер, выходящих из этой вершины. Необходимым условием существования эйлерова пути является связность графа: должен существовать путь из любой вершины в любую. Чтобы выяснить, существует ли эйлеров путь в связном графе, достаточно подсчитать количество вершин нечетной степени в этом графе. Если оно не превосходит 2, то эйлеров путь есть, в противном случае — нет.
Вторая часть этого утверждения очевидна: если есть эйлеров путь, то все вершины графа имеют четную степень, кроме начальной и конечной вершин эйлерова пути (если начальная и конечная вершины совпадают, то степени всех вершин четны).
Доказательство существования эйлерова пути основано на таком простом наблюдении: если есть два замкнутых пути без общих ребер, но с общей вершиной, то их можно объединить в один путь (идем по первому пути до общей вершины, потом обходим второй путь и продолжаем движение по первому). Далее нужно применить индукцию по числу вершин и ребер в графе. Кратко изложим это индуктивное рассуждение (читателю рекомендуется восстановить опущенные детали самостоятельно).
Если все вершины графа  четной степени, то выберем в нем какой-нибудь замкнутый путь
четной степени, то выберем в нем какой-нибудь замкнутый путь  . Выбросив ребра
. Выбросив ребра  из графа
из графа  , получим некоторое количество связных графов
, получим некоторое количество связных графов 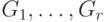 , у которых все степени вершин четные. Так что в каждом из этих графов есть эйлеров путь (по индукции). Каждый из таких графов имеет хотя бы одну вершину на
, у которых все степени вершин четные. Так что в каждом из этих графов есть эйлеров путь (по индукции). Каждый из таких графов имеет хотя бы одну вершину на  (иначе
(иначе  был бы несвязным). Поэтому можно применить изложенную выше конструкцию, чтобы построить из
был бы несвязным). Поэтому можно применить изложенную выше конструкцию, чтобы построить из  и эйлеровых путей в графах
и эйлеровых путей в графах  эйлеров путь в
эйлеров путь в  .
.
Если в графе  есть две1Если у вас получился граф, у которого ровно одна вершина нечетной степени, то проверьте вычисления и найдите ошибку.
вершины нечетной степени, то выберем связывающий их путь
есть две1Если у вас получился граф, у которого ровно одна вершина нечетной степени, то проверьте вычисления и найдите ошибку.
вершины нечетной степени, то выберем связывающий их путь  . Дальнейшее рассуждение остается прежним.
. Дальнейшее рассуждение остается прежним.
Осталось заметить, что и подсчет степени вершины, и проверка связности графа могут быть выполнены за полиномиальное время.
2.3. Рассмотрим предикат 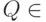 . По определению
. По определению
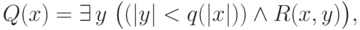
 — полином, а
— полином, а 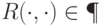 . В другой интерпретации слово
. В другой интерпретации слово  — это сообщение Мерлина, доказывающее истинность
— это сообщение Мерлина, доказывающее истинность 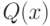 .
.Предположим, что Артур полностью доверяет Мерлину, а тот имеет право отвечать только одним битом (и всегда дает правильный ответ на поставленный вопрос). Тогда Артур может восстановить слово  , выясняя его биты от первого до последнего, следующим образом. Если уже известны первые
, выясняя его биты от первого до последнего, следующим образом. Если уже известны первые  битов, образующие слово
битов, образующие слово  , то Артур может поинтересоваться у Мерлина, существует ли слово
, то Артур может поинтересоваться у Мерлина, существует ли слово 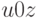 , такое что
, такое что 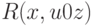 . При положительном ответе
. При положительном ответе 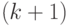 -й бит полагается равным 0, при отрицательном — 1.
-й бит полагается равным 0, при отрицательном — 1.
Если  , то Артур может имитировать Мерлина.
, то Артур может имитировать Мерлина.
2.4 Принадлежность задачи о паросочетаниях классу NP очевидна: Мерлину достаточно разбить мальчиков и девочек на пары, после чего Артур сможет убедиться, что пар ровно  и все выбранные пары согласны танцевать.
и все выбранные пары согласны танцевать.
Доказательство принадлежности P будем проводить, переформулировав задачу в терминах теории графов. Есть двудольный граф (ребра соединяют только вершины из разных долей), нужно проверить, существует ли совершенное паросочетание, т.е. такой набор ребер, что каждая вершина инцидентна ровно одному ребру из набора (если каждая вершина графа инцидентна не более чем одному ребру из набора, то такой набор называется паросочетанием, размер паросочетания — количество входящих в него ребер).
Мы рассмотрим алгоритм, последовательно увеличивающий текущее паросочетание, начиная с пустого. Построение завершается либо совершенным паросочетанием, либо доказательством максимальности размера текущего паросочетания (и тогда совершенного паросочетания в графе нет).
Алгоритм будет использовать для увеличения размера текущего паросочетания построение чередующего пути (это такой путь в графе, который начинается и заканчивается в вершинах, не инцидентных ребрам паросочетания, и проходит попеременно по ребрам, принадлежащим и не принадлежащим паросочетанию). Заменив в паросочетании ребра чередующего пути, стоящие на четных местах, на ребра, стоящие на нечетных местах, мы увеличим размер паросочетания.
Обозначим текущее паросочетание через  , а множество вершин, инцидентных ребрам из
, а множество вершин, инцидентных ребрам из  , — через
, — через 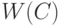 . Предположим, что в графе есть паросочетание
. Предположим, что в графе есть паросочетание  большего размера. Рассмотрим граф
большего размера. Рассмотрим граф  , образованный объединением ребер
, образованный объединением ребер  и
и  . Степени вершин в таком графе не превосходят 2, поэтому его компоненты связности — это пути (возможно, длины 1, т.е. ребра) и циклы (см. рис. 15.2, где сплошными линиями изображены ребра из
. Степени вершин в таком графе не превосходят 2, поэтому его компоненты связности — это пути (возможно, длины 1, т.е. ребра) и циклы (см. рис. 15.2, где сплошными линиями изображены ребра из  , а штриховыми — из
, а штриховыми — из  , на стрелки пока не нужно обращать внимание). Так как
, на стрелки пока не нужно обращать внимание). Так как  имеет больше ребер, чем
имеет больше ребер, чем  , то в
, то в  найдется компонента связности, содержащая больше ребер из
найдется компонента связности, содержащая больше ребер из  , чем из
, чем из  . Такая компонента является, как нетрудно видеть, чередующим путем.
. Такая компонента является, как нетрудно видеть, чередующим путем.
Итак, проверка максимальности заданного паросочетания  равносильна проверке существования чередующего пути. Последнюю можно сделать, например, так. Обозначим доли графа через
равносильна проверке существования чередующего пути. Последнюю можно сделать, например, так. Обозначим доли графа через  и
и  . Ориентируем ребра графа согласно следующему правилу: ребра, входящие в
. Ориентируем ребра графа согласно следующему правилу: ребра, входящие в  , направлены из
, направлены из  в
в  , а все остальные ребра направлены противоположно (эта ориентация также изображена на рис. 15.2). Тогда существование чередующего пути равносильно существованию такой пары вершин
, а все остальные ребра направлены противоположно (эта ориентация также изображена на рис. 15.2). Тогда существование чередующего пути равносильно существованию такой пары вершин 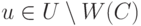 и
и 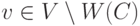 , что из
, что из  в
в  есть ориентированный путь. Существование ориентированного пути с началом и концом в заданных вершинах проверяется способом, описанным в решении задачи 1.17, который работает и в случае ориентированного графа (матрица смежности становится несимметричной, что никак не влияет на вычисления).
есть ориентированный путь. Существование ориентированного пути с началом и концом в заданных вершинах проверяется способом, описанным в решении задачи 1.17, который работает и в случае ориентированного графа (матрица смежности становится несимметричной, что никак не влияет на вычисления).
Итак, мы доказали, что задача о паросочетаниях принадлежит 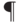 . Описанный выше алгоритм не оптимален, читателю предлагается подумать, как можно его ускорить.
. Описанный выше алгоритм не оптимален, читателю предлагается подумать, как можно его ускорить.
2.5 б) Удобнее описывать сведение 3-КНФ к задаче независимое множество. В этой задаче по графу  и числу
и числу  требуется определить, существует ли в графе
требуется определить, существует ли в графе  множество вершин мощности
множество вершин мощности  , никакая пара вершин которого не связана ребром ( независимое множество ).
, никакая пара вершин которого не связана ребром ( независимое множество ).
Очевидно, что задача клика для графа  эквивалентна задаче независимое множество для дополнительного графа
эквивалентна задаче независимое множество для дополнительного графа  (в дополнительном графе ребра и неребра меняются местами).
(в дополнительном графе ребра и неребра меняются местами).
Возьмем 3-КНФ из  дизъюнкций, в которые входят
дизъюнкций, в которые входят  переменных. Граф, который сопоставляется этой КНФ, имеет
переменных. Граф, который сопоставляется этой КНФ, имеет 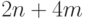 вершин. Каждой переменной
вершин. Каждой переменной  соответствуют две вершины, связанные ребром. Пометим их
соответствуют две вершины, связанные ребром. Пометим их  и
и  (см. рис. 15.3a). Каждой дизъюнкции соответствуют четыре вершины, попарно связанные ребрами между собой. Вершины, соответствующие переменным и дизъюнкциям, связаны между собой так, как показано на рис. 15.3б), (нарисован пример для дизъюнкции
(см. рис. 15.3a). Каждой дизъюнкции соответствуют четыре вершины, попарно связанные ребрами между собой. Вершины, соответствующие переменным и дизъюнкциям, связаны между собой так, как показано на рис. 15.3б), (нарисован пример для дизъюнкции 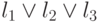 ).
).
Очевидно, что такой граф строится по 3-КНФ полиномиальным алгоритмом.
По построению графа ясно, что любое независимое множество его вершин содержит не более 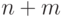 элементов. Докажем, что независимые множества размера
элементов. Докажем, что независимые множества размера 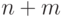 находятся во взаимно однозначном соответствии с выполняющими наборами значений для 3-КНФ, которое задается правилом: если из пары вершин, помеченных
находятся во взаимно однозначном соответствии с выполняющими наборами значений для 3-КНФ, которое задается правилом: если из пары вершин, помеченных  и
и  , в независимое множество входит вершина
, в независимое множество входит вершина  , то в соответствующем этому независимому множеству наборе значений
, то в соответствующем этому независимому множеству наборе значений 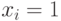 , в противном случае
, в противном случае 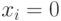 .
.
Из рис. 15.3б) легко усматривается корректность такого соответствия. В независимое множество размера 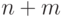 обязана входить хотя бы одна вершина из четверки, соответствующей дизъюнкции. Но это означает, что хотя бы одна из вершин, помеченных
обязана входить хотя бы одна вершина из четверки, соответствующей дизъюнкции. Но это означает, что хотя бы одна из вершин, помеченных  ,
, 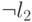 ,
, 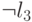 , в это множество не входит. И наоборот, если взять множество
, в это множество не входит. И наоборот, если взять множество  вершин, соответствующих выполняющему набору для 3-КНФ, то оно однозначно дополняется до независимого множества размера
вершин, соответствующих выполняющему набору для 3-КНФ, то оно однозначно дополняется до независимого множества размера 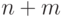 (проверьте по рис. рис. 15.3б), что для каждого набора значений
(проверьте по рис. рис. 15.3б), что для каждого набора значений 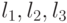 (кроме нулевого набора!) из четверки, соответствующей дизъюнкции, однозначно выбирается вершина, которую можно добавить к
(кроме нулевого набора!) из четверки, соответствующей дизъюнкции, однозначно выбирается вершина, которую можно добавить к  ).
).


