Решения задач
Из раздела 7
7.1 Из доказательства теоремы 7.1 следует, что достаточно научиться реализовывать все операторы вида  ,
, 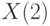 (управляемый двумя q-битами фазовый сдвиг на
(управляемый двумя q-битами фазовый сдвиг на 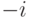 является частным случаем:
является частным случаем:  ). Для алгоритма построения схемы требуется также конструктивное доказательство леммы 7.1.
). Для алгоритма построения схемы требуется также конструктивное доказательство леммы 7.1.
Сперва реализуем управляемый фазовый сдвиг:
![\Lambda(P(\phi))[1,2]=E(\phi)[1], \quad \text{где } P(\phi)=\begin{pmatrix} e^{i\phi}&0\\ 0&e^{i\phi} \end{pmatrix},\quad E(\phi)=\begin{pmatrix} 1&0\\ 0&e^{i\phi} \end{pmatrix}.](/sites/default/files/tex_cache/6c799d1bf24455d9ddd7b5ae3c64b06c.png)
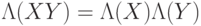 , то остается реализовать операторы
, то остается реализовать операторы  из
из 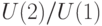 , где
, где 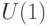 — подгруппа фазовых сдвигов. Можно считать, что
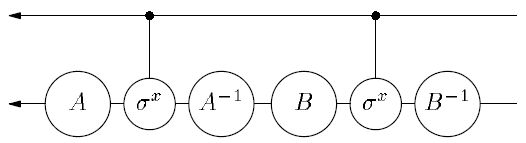
— подгруппа фазовых сдвигов. Можно считать, что  . Эта реализация изображена на рис. 15.5. Используемые в ней операторы
. Эта реализация изображена на рис. 15.5. Используемые в ней операторы  и
и  должны удовлетворять уравнению
должны удовлетворять уравнению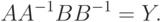 |
( *) |
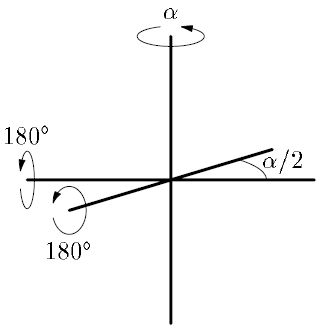
 эквивалентно такому утверждению: любое вращение трехмерного пространства есть композиция двух поворотов на угол
эквивалентно такому утверждению: любое вращение трехмерного пространства есть композиция двух поворотов на угол 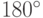 . Доказательство этого утверждения можно усмотреть из рис. 15.6.
. Доказательство этого утверждения можно усмотреть из рис. 15.6.Осталось доказать лемму 7.1 конструктивно. Для начала заметим, что для любых чисел  существует унитарная матрица
существует унитарная матрица  размера
размера  (эффективно вычислимая с любой заданной точностью
(эффективно вычислимая с любой заданной точностью  ), такая что
), такая что

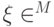 существует последовательность унитарных матриц
существует последовательность унитарных матриц 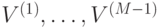 , такая что
, такая что 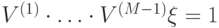 , где
, где 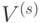 действует на подпространстве
действует на подпространстве  (как матрицы в условии леммы 7.1) и оставляет неизменными остальные базисные векторы.
(как матрицы в условии леммы 7.1) и оставляет неизменными остальные базисные векторы.Пусть теперь задана унитарная матрица  размера
размера  . Умножая
. Умножая 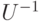 слева на подходящие матрицы
слева на подходящие матрицы 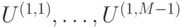 , можно перевести первый столбец в вектор
, можно перевести первый столбец в вектор 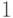 . При этом столбцы остаются ортогональными, поэтому первая строка переходит в
. При этом столбцы остаются ортогональными, поэтому первая строка переходит в 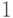 . Действуя таким же образом с остальными столбцами, получаем набор матриц
. Действуя таким же образом с остальными столбцами, получаем набор матриц  \, (
\, ( 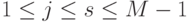 ) (где
) (где  действует на
действует на  и
и  ), удовлетворяющий условию
), удовлетворяющий условию
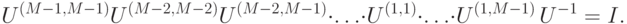
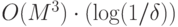 .
.7.2 Неравенство (7.6) следует из цепочки неравенств, справедливых для любого 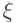 :
:
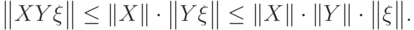
Для доказательства равенства (7.7) заметим, что собственные числа операторов 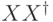 и
и 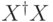 совпадают.
совпадают.