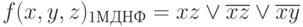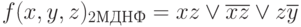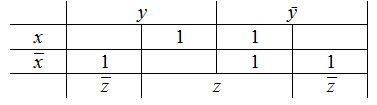Минимизация логических функций
Пример 3.5.
Получить методом диаграмм Вейча минимальную ДНФ следующей логической функции:
f(x,y,z)СДНФ= ?(0,1,2,5,7)
Решение
Этап 1.
Занести значение функции на диаграмму Вейча. В связи с тем что ФАЛ задана в виде сокращенной записи совершенной дизъюнктивной нормальной формы, для ее представления в виде диаграммы Вейча целесообразно использовать вид этой диаграммы, представленный на Рис. 3.1, а. При этом, так как по заданию предполагается получение лишь минимальной дизъюнктивной нормальной формы, для улучшения восприятия диаграммы можно отметить лишь те ячейки, которые соответствуют конституэнтам единицы, предполагая, что ячейки, оставшиеся незаполненными, соответствуют нулевым значениям ФАЛ:
Этап 2.
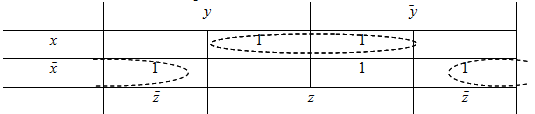
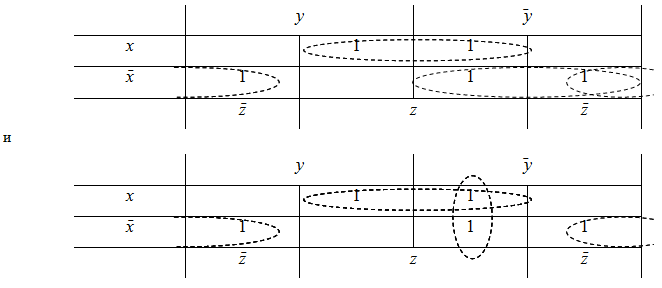
Отметить на диаграмме 1-клетки, входящие в единственныйm куб. При этом одна 1 клетка может входить в несколько m кубов одновременно. Разорванный овал соответствует покрытию соседних клеток при представлении диаграммы Вейча в виде цилиндра с соединенными левой и правой колонками:
Этап 3.
Не вошедшую ни в один из m-кубов 1-клетку можно включить в один из 2-кубов либо с 1 клеткой, стоящей справа от нее, либо с 1 клеткой, стоящей выше нее. Так как оба альтернативных m-куба имеют одинаковый размер, то в результате получим две минимальные дизъюнктивные нормальные формы:
Этап 4.
Представить полученные m-кубы в виде минимальных дизъюнктивных нормальных форм: