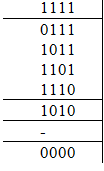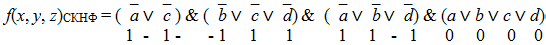Минимизация логических функций
Пример 3.3.
Минимизировать ФАЛ, заданную в виде совершенной конъюнктивной нормальной формы, методом Квайна – Мак-Класки:
f(a,b,c,d)СДНФ= ?(0,7,10,11,13,14,15)
Решение
Последовательность и содержание этапов, выполняемых при минимизации заданной в СКНФ логической функции, эквивалентны аналогичным этапам, выполнявшимся при минимизации логической функции, заданной в СДНФ (см. примеры 3.1 и 3.2).
Этап 1
Записать двоичное представление наборов, образующих СКНФ данной функции: (0000, 0111, 1010, 1011, 1101, 1110, 1111)
Этап 2
Разбить полученные коды на группы, содержащие одинаковое количество нулей в коде. ДляФАЛ, зависящих от n переменных, таких групп может быть n+1 (ни одного нуля в коде, один нуль, два нуля, ... , n нулей в коде). Расположить группы по возрастанию количества нулей. Если количество получившихся групп меньше n+1, то отсутствующие группы помечаются как пустые:
Этап 3
Сравнить каждый код из одной группы с каждым кодом из соседних групп. Если найдены два кода, отличающихся только в одном разряде (то есть они могут "склеиваться" между собой согласно (3.1.4)), то пометить их каким-либо особым символом, например, "*", и в новую группу поместить код, сохраняющий значение в совпадающих разрядах и имеющий какой-либо особый символ, например "-", на месте несовпадающего разряда. При этом образуется n-1 новая группа кодов.
Эта процедура повторяется для вновь образованных групп до тех пор, пока возможна процедура "склеивания" элементов соседних групп. Максимально возможное число шагов на этом этапе равно n. На всех шагах, начиная со второго, необходимо следить за тем, чтобы два "склеиваемых" кода представляли собой термы, зависящие от одних и тех же логических переменных, то есть знаки "-" у них должны находиться в одних и тех же позициях. При появлении в одной группе нескольких одинаковых термов для дальнейшего анализа следует оставить лишь один из них.
Результатом этого этапа является получение всех первичных имплицент функции и ее сокращенной конъюнктивной нормальной формы.
Этап 4
Составить имплицентную матрицу, представляющую собой таблицу, которая в качестве заголовков столбцов имеет все конституэнты нуля исходной функции, а в качестве заголовков строк – первичные имплиценты.
В ячейку таблицы ставится какой-либо отличительный символ, например "+", если первичная имплицента, стоящая в заголовке строки, является собственной частью конституэнты нуля, стоящей в заголовке столбца. В противном случае ячейка остается пустой:
Простейший контроль правильности заполнения таблицы может быть проведен аналогично примеру 3.1.
Этап 5
Найти существенные имплиценты.
Для этого в таблице отыскиваются столбцы, содержащие ровно одну помеченую ячейку. Имплиценты, содержащиеся в заголовке строк таких ячеек, являются существенными и подлежат обязательному включению в состав минимальной формы.
Из дальнейшего рассмотрения исключаются столбцы, содержащие пометки в строках, соответствующих существенным имплицентам.
Для рассматриваемой функции все содержащиеся в заголовках строк минтермы будут существенными, так как первичная имплицента 1-1- необходима для покрытия макстермов 1010, 1011, 1110 и 111 исходного набора, имплиценнта -111 – для покрытия макстерма 0111, имплиценнта 11-1 – для покрытия макстерма 1101, а имплицента 0000 необходима для покрытия такого же макстерма в исходном наборе.
Таким образом, получим единственный набор, покрывающий все макстермы, составляющие совершенную конъюнктивную нормальную форму заданной функции. В связи с этим отсутствует этап, аналогичный этапу 6 в примерах 3.1 и 3.2.
Полученная единственная минимальная конъюнктивная нормальная форма имеет следующий вид: