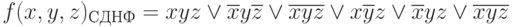Минимизация логических функций
Метод непосредственных преобразований логических функций заключается в том, что логическая функция подвергается упрощению непосредственно с помощью аксиом и теорем алгебры логики.
Некоторые из таких эквивалентностей мы рассматривали выше. Например, правила де Моргана, склеивания, поглощения. Первое из указанных правил, обычно используется для приведения функции к виду, удобному для последующих преобразований. Операции склеивания и поглощения в явном виде позволяют уменьшить количество символов в выражении.
Однако этот метод обладает существенными недостатками:
- как правило, такие преобразования требуют громоздких выкладок;
- процесс упрощения логической функции не является алгоритмическим; во многом он зависит от мастерства и опыта разработчика;
- и, самое главное, результат преобразования не гарантирует получения минимальной формы дизъюнктивной или конъюнктивной ФАЛ.
Отметим, что получение минимальной формы в своей основе содержит совершенную (дизъюнктивную или конъюнктивную) нормальную форму
Приведение дизъюнктивной (или конъюнктивной) формы записи ФАЛ к совершенному виду проходит на основе формул (1.1) и (1.2), только правые и левые их части целесообразно поменять местами (в этом случае данные формулы обычно называются операциями развертывания). Тогда ДНФ, в которой не все члены являются элементарными конъюнкциями, приводится к СДНФ следующим образом.
Пусть некоторая ДНФ имеет следующий вид:
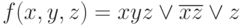
Так как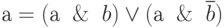 
, то исходную функцию можно представить как
Убирая повторяющиеся члены, чего требует запись функции в совершенном виде, на основе свойства дизъюнкции a V a V ... V a = a, получим:
