Минимизация логических функций
Пример 3.6. Минимизировать функцию, заданную в виде СКНФ:
f(a,b,c,d)СКНФ= ?(2,3,5,6,7,10,11,13,14)
Минимальная форма:
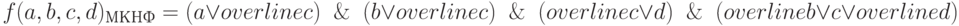
Пример 3.7. На этом примере хотелось бы продемонстрировать необходимость использования одного из основных принципов построения минимальных форм, а именно, поиск существенных импликант на первоначальном этапе анализа диаграммы.
Пусть необходимо найти минимальную дизъюнктивную нормальную форму для логической функции, заданной в виде СДНФ:
f(a,b,c,d)СДНФ= ?(0,2,3,7,9,10,11,14)
Решение
Этап 1.
Занести значение функции на диаграмму Вейча для четырех переменных:
Этап 2.
Сначалапокажем, что бросающееся в глаза решение, связанное с использованием одного 3-куба и четырех 2-кубов, не обеспечивает получения минимальномой ДНФ:
Решение на данном этапе должно проходить следующим образом.
Отметить на диаграмме 1-клетки, входящие в единственный m-куб:
На диаграмме они отмечены полужирным шрифтом и будут являться существенными импликантами.
Этап 3.
Так как все 1-клетки вошли в какой-либо из m-кубов, то осталось только записать минимальную ДНФ:
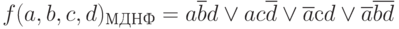
Необходимо обратить внимание на то, что, как указывалось выше, не следует начинать поиск покрытий с отыскания m-кубов максимально возможной площади. Так, в данном случае 1-клетки (2,3,10,11) можно было бы включить в 2-куб (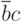 ). Однако при этом все равно сохранилась бы необходимость покрытия остальных 1 клеток 1-кубами. Поэтому данный 2 куб в окончательный вариант покрытия входить не должен.
). Однако при этом все равно сохранилась бы необходимость покрытия остальных 1 клеток 1-кубами. Поэтому данный 2 куб в окончательный вариант покрытия входить не должен.
Следует отметить, что метод минимизирующих карт дает быстрое и наглядное решение для функции от небольшого числа переменных (обычно, он используется для минимизации ФАЛ от трех либо четырех переменных, в очень редких случаях при достаточном опыте разработчика он может быть использован для минимизации функции от пяти переменных).
В то же время метод Квайна – Мак-Класки хорошо работает при минимизации логической функции от произвольного числа аргументов, но не обладает простотой и наглядностью метода минимизирующих карт.