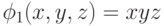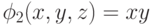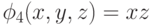Минимизация логических функций
Минимизация логических функций
Преобразование логических функций с целью упрощения их аналитического представления называются минимизацией.
Понятие "упрощение" требует определенных договоренностей, что под этим будет пониматься. Упрощение можно рассматривать с точки зрения числа переменных в получаемоq эквивалентной функции, уменьшения количества отрицаний в результирующем выражении, более простой схемотехнической реализации при переводе получающейся ФАЛ на уровень интегральных микросхем и так далее.
Мы будем считать, что дизъюнктивная или конъюнктивная нормальная форма являются минимальными, если они содержат наименьшее суммарное число переменных среди всех ДНФ или КНФ, эквивалентных ей. При этом количество отрицаний над переменными учитывать не будем.
Методы минимизации можно разделить на несколько типов:
- Метод непосредственных преобразований логических функций.
- Метод неопределенных коэффициентов.
-
Аналитические методы (метод Квайна11Квайн, Уиллард Ван Орман — американский философ, логик и математик, метод Квайна – Мак-Класки).
- Метод минимизирующих карт (карты Карно, диаграммы Вейча).
Рассмотрим их более подробно. Рассмотрение будем проводить на основе дизъюнктивных нормальных форм. Для КНФ теоретические рассуждения будут аналогичными.
В то же время, иллюстрировать соответствующие положения будем как на примерах дизъюнктивны, так и конъюнктивных форм.
Если некоторая логическая функция  равна нулю на тех же наборах, на которых равняется нулю другая функция f, то говорят, что функция
равна нулю на тех же наборах, на которых равняется нулю другая функция f, то говорят, что функция  входит в функцию f. Другими словами, функция
входит в функцию f. Другими словами, функция  входит в функцию f тогда, когда она накрывает нулями все нули функции f, а единицы функции f могут быть накрыты как нулями, так и единицами функции
входит в функцию f тогда, когда она накрывает нулями все нули функции f, а единицы функции f могут быть накрыты как нулями, так и единицами функции  .
.
Очевидно, что ФАЛ "Константа ноль" входит во все функции, а в ФАЛ "Константу единица" входят все функции.
Функцию  , входящую в данную функцию f, называют ее импликантой.
, входящую в данную функцию f, называют ее импликантой.
Простыми (первичными) импликантами (имплицентами для КНФ) логической функции f называют такие элементарные произведения или элементарные суммы (для имплицент), которые сами входят в данную функцию, но никакая собственная частьэтих произведений (сумм) не входит в функцию f.
Собственной частью называют произведение, полученное путем исключения из данного произведения одного или нескольких сомножителей.
Примеры этих определений показаны в Табл. 3.1.