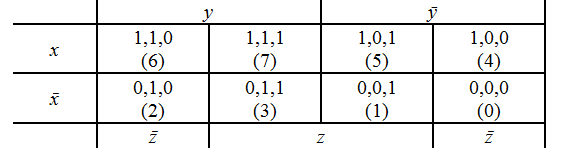Минимизация логических функций
Метод минимизирующих карт (карты Карно, диаграммыВейча)
Карты Карно (их разновидностью являются диаграммы Вейча) являются графическим представлением таблиц истинности. Поэтому они строятся или по таблице истинности анализируемой функции, или же по ее СДНФ.
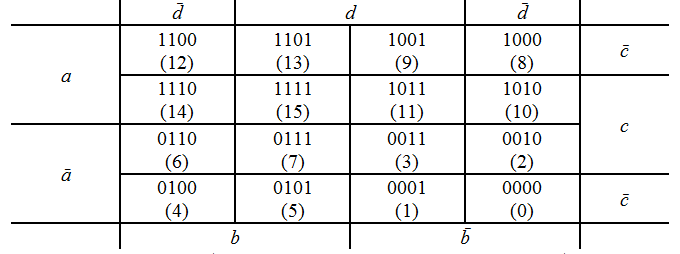
Диаграммы Вейча представляет собой прямоугольник, разбитый на ячейки, число которых равно общему числу наборов для данной функции n переменных, то есть оно равно 2n. Так, для функции 3-х переменных ячеек будет 8, для 4-х переменных – 16 и т.д.
Каждая ячейка соответствует определенному набору, или терму, причем наборы располагаются так, чтобы соседние наборы, или термы как по горизонтали, так и по вертикали, отличались бы только значением одной переменной: в одной ячейке она была бы в прямом виде, а в соседней – с инверсией. Причем надо учесть, что ячейки, расположенные на противоположных концах каждой строки или столбца, также являются соседними.
Функцию в СДНФ наносят на карту, отмечая, например, знаком "1" ячейки, соответствующие тем наборам, на которых ФАЛ равна единице, т.е. в СДНФ функции эта ячейка соответствует одному изееминтермов. Остальные ячейки отмечаются знаком "0".
Если данную таблицу рассматривать как цилиндр, образованный соединением первой и последней колонок, то тогда склеивающиеся между собой конституэнты единицы или нуля в диаграммах Вейча будут расположены в соседних клетках. При этом прямоугольники, покрывающие 2kсоседних клеток, описывают имликанту (имплиценту), имеющую ранг (n-k), где n – число переменных, от которых зависит функция.
Клетки, содержащие в диаграмме Вейча единицы, будем называть 1-клетками, а клетки, содержащие нули – 0-клетками.
Основное свойство диаграмм Вейча заключается в том, что любая первичная импликанта ранга (n-m) образует на ней прямоугольник и только прямоугольник 1-клеток площадью 2m, где n – количество переменных, от которых зависит функция. Такие прямоугольники называют m-кубами (m=0,1,…,n.; 0-кубу соответствует минтерм, а n-кубу – константа "единица"). Так любая пара единиц в соседних клетках диаграммы Вейча для логической функции трех переменных представляется импликантой второго ранга. Четыре единицы, образующие прямоугольник, выражаются одной переменной (с отрицанием или без него).
Чтобы записать первичную импликанту, представляющую собой некий m-куб на диаграмме Вейча, необходимо просто составить конъюнкцию тех переменных, которые в пределах данного m-куба сохраняют постоянные значения (только прямые или только инверсные).
Получение минимальной ДНФ с помощью диаграмм Вейча сводится к отысканию минимального числа m-кубов максимально-го размера, состоящих из 1-клеток, и составлению дизъюнкции импликант, соответствующих этим m-кубам (каждая 1-клетка должна войти хотя бы в один m-куб, любая 1-клетка может входить одновременно в несколько различных m-кубов).
При получении МДНФ с помощью диаграммы Вейча необходимо обратить внимание на следующее:
- m-кубу, покрывающему2m 1-клеток, соответствует первичная импликанта, не зависящая от m переменных, причем исключаются те m переменных, которые в прямоугольной области на диаграмме Вейча, состоящей из 1-клеток, имеют различное значение (прямое и инверсное);
- прямоугольные области на диаграмме Вейча, используемые при минимизации, могут состоять только из 2m соседних клеток, где m = 0,1,…,n;
- каждая клетка на диаграмме Вейча, вне зависимости от способа разметки этой диаграммы, имеет ровно n соседних клеток; в связи с этим диаграмма Вейча представляется нанесенной на поверхность соответствующего тела (цилиндра – для случая трех переменных, тора – для случая четырех переменных);
- поиск минимального покрытия 1-клеток следует начинать с выбора тех 1-клеток, которые могут войти в один и только один m-куб; если после этого на диаграмме остаются 1 клетки, не вошедшие ни в один из m-кубов, то следует рассмотреть несколько вариантов покрытий этих клеток; с целью минимизации результата оставшиеся 1-клетки покрываются, по возможности, m-кубами максимального размера.
Получение минимальной КНФ проводится аналогичным образом по отношению к 0 клеткам.