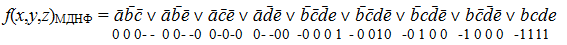Минимизация логических функций
Пример 3.5.
Минимизировать методом Квайна – Мак-Класки следующую логическую функцию:
f(a,b,c,d,e)СДНФ = ?(0,1,2,3,4,6,8,10,12,15,17,18,20,24,31)
Решение
Этап 1
Выписать двоичное представление наборов, образующих СДНФ данной функции: (00000, 00001, 00010, 00011, 00100, 00110, 01000, 01010, 01100, 01111, 10001, 10010, 10100, 11000, 11111).
Этапы 2 и 3.
Разбить полученные двоичные коды на группы, содержащие одинаковое количество единиц в коде. Расположить группы по возрастанию (или убыванию) количества единиц. Выполнить склейку кодов из соседних групп.
Для данной ФАЛ отсутствует элемент 3-группы, поэтому помечаем эту группу как пустую.
| 00000* |
0000-* 000-0* 00-00* 0-000* |
000 - - 000 - - 00 - - 0 00- - 0 0- - 00 0-0-0 0- -00 |
|
00001* 00010* 00100* 01000* |
000-1* 0001-* 00-10* 0-010* 001-0* 0-100* 010-0* 01-00* -0001 -0010 -0100 -1000 |
– |
|
00011* 00110* 01010* 01100* 10001* 10010* 10100* 11000* |
– | – |
| – | – | – |
| 01111* | -1111 | – |
| 11111* | – | – |
Этап 4
Составить импликантную матрицу:
| Первичные импликанты | Конституэты единицы | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 00000 | 00001 | 00010 | 00011 | 00100 | 01000 | 01010 | 01100 | 01111 | 10001 | 10010 | 10100 | 11000 | 11111 | ||
| 000-- | + | + | + | + | |||||||||||
| 00--0 | + | + | + | + | |||||||||||
| 0-0-0 | + | + | + | + | |||||||||||
| 0--00 | + | + | + | + | |||||||||||
| -0001 | + | + | |||||||||||||
| -0010 | + | + | |||||||||||||
| -0100 | + | + | |||||||||||||
| -1000 | + | + | |||||||||||||
| -1111 | + | + | |||||||||||||
Этапы 5 и 6
Анализ импликантной матрицы показывает, что все полученные первичные импликанты являются существенными и, следовательно, рассматриваемая ФАЛ имеет единственную минимальную дизъюнктивную нормальную форму:
Таким образом, использование метода Квайна – Мак-Класки позволяет проводить минимизацию логических функций от произвольного количества аргументов.