Минимизация логических функций

Минимизация неполностью определенных ФАЛ

Неполностью определенной ФАЛ от n переменных называется функция, заданная на множестве наборов входных переменных, меньше чем 2ⁿ.

Такая ситуация в вычислительной технике встречается в двух случаях:

• какие-либо из наборов переменных никогда не могут появиться, и поэтому значение функции на этих наборах определять не имеет смысла. Например, в качестве входных переменных выступают показания часов. Тогда наборы от 12 до 15 (при 4-разрядном представлении) никогда в реальности не встретятся;
• выход элемента, реализующего какую либо логическую функцию, поступает на вход элемента, выполняющего операцию конъюнкции. На второй вход этого элемента поступает значение, о котором известно, что оно на каких-либо наборах принимает значение "0". В этом случае состояние выхода первого элемента на данных наборах значения иметь не будет, так как на выходе конъюктора всё равно будет состояние логического нуля.

Пусть функция f(x₁, x₂,..., x_n) не определена на p наборах аргументов. Тогда не полностью определенную функцию 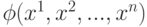будем считать эквивалентной функции 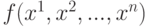, если ее значения на тех наборах, на которых функция 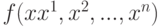определена, совпадают.

Очевидно, существует 2^р различных функций, эквивалентных исходной. Задача минимизации состоит в выборе такой эквивалентной 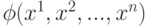, которая имеет простейшую форму.Проведем такую минимизацию по методу диаграмм Вейча.

Каждая ячейка на диаграмме Вейча соответствует определенному значению логической функции для того или иного набора аргументов. Если известно, что в некоторых случаях какой-то набор аргументов появиться не может или же если он появится, то значение функции на этом наборе по тем или иным причинам, не существенно для работы всего устройства, то для таких случаев нет необходимости определять значение функции по таблице истинности. В таких случаях говорят о неполностью определенных ФАЛ.

На диаграмме Вейча неопределенное условие, как правило, обозначается прочерком или каким-либо другим знаком, отличным от "0" и "1" в соответствующей ячейке. Такие ячейки могут произвольным образом включаться как в группу единичных, так и в группу нулевых ячеек, или же вообще никуда не включаться.