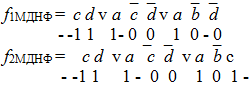Минимизация логических функций
Минимизация логических функций методом Квайна – Мак-Класки
Как вы,надеюсь, заметили (особенно если не просто читали данный материал, а пытались прорабатывать его самостоятельно на различных примерах), метод, основанный на теореме Квайна, имеет два существенных недостатка.
Во-первых, на первоначальном этапе минимизации при получении сокращенной дизъюнктивной или конъюнктивной формы ФАЛ приходится каждый член исходного представления функции, а затем и результаты неполного склеивания постоянно сравнивать со всеми другими импликантами, составляющими функцию, которых становится все больше и больше. И лишь на стадии поглощения количество импликант в общем случае сокращается.
Ко второму недостатку следует отнести сложность получения тупиковых форм по импликантной матрице в том случае, если после выделения существенных импликант остаются непокрытыми несколько столбцов, соответствующих минтермам исходной совершенной нормальной формы логической функции.
В 1956 году Эдвард Мак-Класки22Уиллард Ван Орман Куайн (англ. Willard Van Orman Quine) — американский философ, логик и математик. Родился 25 июня 1908 года в Акроне, штат Огайо. Умер 25 декабря 2000 года в Бостоне, штат Массачусетс, в возрасте 92 лет.доработал данный метод. Он предложил ряд модификаций, который существенно сократили количество необходимых сравнений при получении сокращенной нормальной формы и максимально адаптировали его для компьютерной минимизации логических функций.
Суть этих предложений (применительно к ФАЛ, представленным в виде дизъюнктивных нормальных форм) заключается в следующем.
- Каждая элементарная конъюнкция в СДНФ упорядочивается по какому-либо принципу, например, по алфавиту, и представляется своим двоичным набором, где переменной, входящей в произведение в прямом виде ставится в соответствие единица ("1"), в инверсном – нуль ("0").
- Вся совокупность номеров наборов разбивается на группы в зависимости от числа единиц, имеющихся в номерах наборов (0-группа, 1-группа, 2-группа и т.д.). Если в исходной совокупности отсутствуют наборы с определённым числом единиц (например, с одной единицей), то соответствующая группа (в данном случае, 1-группа) все равно создается, но с нулевым количеством элементов.
- Сравниваются элементы двух соседних группы, отличающиеся на одну единицу.При этом устанавливается возможность склейки двух наборов из этих групп, для этих наборов делается необходимая пометка и пишется результат склейки.
- Процесс продолжается до тех пор, пока возможны склейки.
- Все несклееные наборы, а также конечные результаты склейки дают представление ФАЛ в виде сокращенной нормальной формы.
Замена символьного представления ФАЛ на двоичное облегчает ее компьютерную обработку, а разбиение элементарных конъюнкций в СДНФ на группы существенно сокращает перебор вариантов для обнаружения наборов, которые потенциально могут склеиться друг с другом.
Это связано с тем, что склеиться могут лишь те набору, которые зависят от одних и тех же переменных и отличаются лишь в одной из них. Поэтому целесообразно рассматривать лишь наборы, которые отличаются ровно на одну единицу или ноль, то есть наборы соседних групп. Из этого вытекает и необходимость введения "пустых" групп, а также то свойство, что элемент 0-группы "склеится" со всеми элементами 1-группы, а элемент группы из всех единиц "склеиться" со всеми элементами предшествующей группы.
Пример 3.2.
Минимизировать методом Квайна – Мак-Класки следующую логическую функцию:
f(a,b,c,d)СДНФ = ?(3,7,8,10,11,12,15)
Решение
Этап 1
Выписать двоичное представление наборов, образующих СДНФ данной функции: (0011, 0111, 1000, 1010, 1011, 1100, 1111)
Этап 2.
Разбить полученные двоичные коды на группы, содержащие одинаковое количество единиц в коде. Для ФАЛ, зависящих от n переменных, таких групп может быть n+1 (ни одной единицы в коде, одна единица, две единицы, ... , n единиц в коде). Расположить группы по возрастанию (или убыванию) количества единиц.
Для данной ФАЛ отсутствует элемент 0-группы, поэтому помечаем эту группу как пустую:
Этап 3
Сравнить каждый код из одной группы с каждым кодом из соседних групп. Если найдены два кода, отличающиеся только в одном разряде (то есть они могут "склеиваться"), то пометить эти коды каким-либо особым символом, например "*", и в новую группу поместить код, сохраняющий значение в совпадающих разрядах и имеющий какой-либо особый символ, например "-", на месте несовпадающего разряда. При этом образуется n-1 новая группа кодов. Если код попадает в несколько "склеек", то он символом * может помечаться только один раз.
Эта процедура повторяется для вновь образованных групп до тех пор, пока возможна процедура "склеивания" элементов соседних групп. Максимальное возможное число шагов на этом этапе равно n. На всех шагах, начиная со второго, необходимо следить за тем, чтобы два "склеиваемых" кода представляли собой термы одного ранга изависили от одних и тех же логических переменных, то есть знаки "-" у них должны находиться в одних и тех же позициях. При появлении в одной группе нескольких одинаковых импликант для дальнейшего анализа следует оставить лишь одну из них (x V x = x).
Последовательность выполнения шагов этапа 3:
Таким образом, сокращенной дизъюнктивной нормальной формой исходной функции будет конъюнкция набора (--11) из последнего столбца преобразований, а также наборов (10-0), (1-00), (101) из предыдущих столбцов, которые не имеют пометок и, следовательно, не попали в "склейки" на последующих этапах.
Собственно, на этом модификация, предложенная Мак-Класки, завершена: мы получили сокращенную дизъюнктивную нормальную форму логической функции. Дальнейшие действия по получению тупиковой и минимальной нормальной формы ФАЛ можно проводить как представив полученную СкНФ в символьном виде, так и продолжая работать с ее двоичным представления, а перейдя к символьному представлению функции лишь в самом конце. Поступим в этом примереименно так.
Этап 4
Составить импликантную матрицу.
| Первичные импликанты | Конституэты единицы | ||||||
|---|---|---|---|---|---|---|---|
| 0011 | 0111 | 1000 | 1010 | 1011 | 1100 | 1111 | |
| --11 | + | + | + | + | |||
| 10-0 | + | + | |||||
| 1-00 | + | + | |||||
| 101- | + | + | |||||
| -111 | + | + | |||||
Этап 5
Найти существенные импликанты функции.
Для рассматриваемой функции существенными импликантами будут - -11 и 1-00, так как только первичная импликанта --11 позволяет покрыть минтерм 0011 исходного набора, а первичная импликанта 1-00 необходима для покрытия минтерма 1100.
| Первичные импликанты | Конституэты единицы | ||||||
|---|---|---|---|---|---|---|---|
| 0011 | 0111 | 1000 | 1010 | 1011 | 1100 | 1111 | |
| --11 | + | + | + | + | |||
| 10-0 | + | + | |||||
| 1-00 | + | + | |||||
| 101- | + | + | |||||
| -111 | + | + | |||||
Этап 6
Найти тупиковые дизъюнктивные нормальные формы и выбрать из них минимальные ДНФ.
Рассматриваемая функция имеет две различные тупиковые, они же минимальные дизъюнктивные формы:
Обе тупиковые формы содержат одинаковое количество символов. Поэтому по нашему критерию их обе можно считать минимальными дизъюнктивными нормальными формами исходной функции.
Как вы, наверное, заметили, в примерах 3.1 и 3.2 мы минимизировали одну и ту же логическую функцию, но в примере 3.2 этот процесс прошел гораздо быстрее.