|
Добрый день можно поинтересоваться где брать литературу предложенную в курсе ?Большинство книг я не могу найти в известных источниках |
Оценка эффективности генетических алгоритмов поиска масок
В генетическом алгоритме в первой серии экспериментов была использована фитнес-функция (29.7). Результаты экспериментов, касающиеся динамики нахождения решения задачи минимизации каждой из индивидуальных масок для схем из набора ISCAS'89, приведены в табл. 30.6.
| Схема |  |
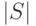 |
Объем полной ДИ | Результат после 40 поколений | Результат после 60 поколений | Результат после 80 поколений | |||
|---|---|---|---|---|---|---|---|---|---|
| Объем маски | 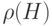 |
Объем маски | 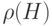 |
Объем маски | 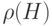 |
||||
| S400 | 195 | 13284 | 2590380 | 586 | 1,492 | 693 | 1,226 | 950 | 1,000 |
| S820 | 713 | 21185 | 15104905 | 4055 | 1,547 | 5788 | 1,250 | 7152 | 1,000 |
| S832 | 720 | 21603 | 15554160 | 4483 | 1,547 | 5787 | 1,267 | 7535 | 1,000 |
| S1488 | 1360 | 22230 | 30232800 | 7497 | 1,618 | 9062 | 1,309 | 11539 | 1,000 |
| S1494 | 1361 | 23655 | 32194455 | 8520 | 1,641 | 9965 | 1,309 | 12491 | 1,000 |
Данные из этой таблицы получены с применением выбора линейным ранжированием и однородного кроссовера, при которых генетический алгоритм показал наилучшие результаты.
Вторая серия экспериментов ставилась для задачи минимизации объема совокупности индивидуальных масок генетическим алгоритмом с фитнес-функцией (29.8). Так же как и в предыдущей серии экспериментов, наилучшие результаты были получены при отборе линейным ранжированием и использовании однородного кроссовера. Результаты этой серии экспериментов представлены в табл. 30.7.
| Схема |  |
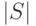 |
Объем полной ДИ | Результат после 40 поколений | Результат после 60 поколений | Результат после 80 поколений | |||
|---|---|---|---|---|---|---|---|---|---|
| Объем маски | 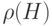 |
Объем маски | 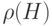 |
Объем маски | 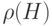 |
||||
| S400 | 195 | 13284 | 2590380 | 795 | 1,667 | 917 | 1,308 | 1149 | 1,000 |
| S820 | 713 | 21185 | 15104905 | 7673 | 1,976 | 11069 | 1,443 | 12915 | 1,000 |
| S832 | 720 | 21603 | 15554160 | 7061 | 2,008 | 11031 | 1,447 | 13817 | 1,000 |
| S1488 | 1360 | 22230 | 30232800 | 13587 | 1,956 | 17396 | 1,479 | 21074 | 1,000 |
| S1494 | 1361 | 23655 | 32194455 | 13507 | 1,989 | 18419 | 1,481 | 22520 | 1,000 |
Эксперименты с ДИ для реальных устройств показали, что оптимальная численность популяции для предложенных ПГА - 100 особей, а для получения приемлемого решения достаточно 70 поколений.
На следующем этапе были проведены исследования для оценки ускорения ГА при использовании многопроцессорных ЭВМ. Наиболее трудоемким этапом в ПГА для поиска маски является получение значения фитнес-функции для каждой хромосомы. В следующих экспериментах была сделана попытка достичь простого ускорения этого этапа, производя вычисления фитнес-функции одновременно для нескольких хромосом. Результаты, приведенные в табл. 30.9, были получены на ЭВМ с ЦП Intel Core2Duo 2,33ГГц, 2 Гб ОЗУ. Эксперименты проводились для ДИ полученной для ДУ из каталога ISCAS'85 [4] и ISCAS'89 [2] при моделировании одиночных неисправностей с помощью тестовых последовательностей HITEC [3]. Характеристики диагностической информации для этих ДУ приведены в табл. 30.8. Была взята численность популяции - 900 особей, а процесс эволюции прерывался при достижении 300 поколений.
| Схема | 
|
 |
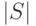 |
 |
 |
Объем ДИ, бит |
|---|---|---|---|---|---|---|
| С499 | 41 | 32 | 985 | 184 | 5888 | 5799680 |
| С1355 | 41 | 32 | 2027 | 198 | 6336 | 12843072 |
| С2670 | 233 | 140 | 4111 | 102 | 14280 | 58705080 |
| S298 | 3 | 6 | 178 | 322 | 1932 | 343896 |
| S344 | 9 | 11 | 241 | 127 | 1397 | 336677 |
| S526 | 3 | 6 | 139 | 2258 | 13548 | 1883172 |
| S1488 | 8 | 19 | 1360 | 1170 | 22230 | 30232800 |
| S2081 | 10 | 1 | 56 | 100 | 100 | 5600 |
| Схема | Время работы алгоритма с использованием одного процессора | Время работы алгоритма с использованием двух процессоров |
|---|---|---|
| S2081 | 14 с | 9 с |
| S298 | 7 мин 16 с | 4 мин 03 с |
| S344 | 17 мин 11 с | 9 мин 44 с |
| S526 | 23 мин 30 с | 14 мин 03 с |
Из приведенных в этой таблице данных следует, что при распараллеливании ГА в системе, имеющей два процессора, время работы алгоритма сокращается практически вдвое.
Также были поставлены эксперименты по поиску масок с помощью ГА на многомашинных системах. В экспериментах использовались 4 базовых ЭВМ со следующими характеристиками: ЦП Intel Pentium D 2.8 ГГц (2 ядра), 1 ГБ ОЗУ, которые были объединены в локальную вычислительную сеть с пропускной способностью 100 Мбит/сек. Результаты этих экспериментов приведены в табл. 30.10.
| Схема | Время работы алгоритма с использованием одной двухпроцессорной машины | Время работы алгоритма с на четырех двухпроцессорных машинах | Ускорение |
|---|---|---|---|
| S1488 | 4 час 10 мин | 1 час 14 мин 57 с | 3,33 |
| С499 | 53 мин 17 с | 17 мин 41 с | 3,01 |
| С1355 | 5 час 15 мин 50 с | 1 час 21 мин 42 с | 3,86 |
| С2670 | 13 час 57 мин | 3 час 43 мин 15 с | 3,74 |
Данные из этих таблиц были получены при количестве этапов эволюции - 300 поколений и численности популяции: для схемы С2670 - 100 особей, для всех остальных ДУ - 500 особей.
Эксперименты показали, что практический смысл использования многомашинных систем имеют только вычисления со значительным объемом ДИ. В этом случае временные затраты на передачу данных по сети и синхронизацию становятся незначительными по сравнению с затратами на сами вычисления. В ходе экспериментов было установлено, что запуск на многомашинных системах ГА для поиска маски ДИ объема, не превышающего 10 мегабит, не дает преимущества во времени работы алгоритма по сравнению с запусками на одномашинной системе.
Ключевые термины:
Оценка эффективности ГА - получение совокупности показателей, характеризующих качественно и/или количественно требуемый объем памяти и быстродействие генетического алгоритма.
Вычислительная сложность поиска маски- емкостные и временные оценки ГА в терминах размерности популяций, обрабатываемых ГА, и количества битов, необходимых для хранения информации об одной особи популяции.
Экспериментальные данные - совокупность результатов численных экспериментов с различными цифровыми схемами, связанных с применением ГА для поиска масок с целью сокращения объема полной ДИ упомянутых схем.
Краткие итоги:
В лекции приведены многочисленные статистические данные, подтвердающие высокую эффективность описанных в предыдущей лекции генетических алгоритмов поиска различных разновидностей масок.
Вопросы и упражнения
- Приведите теоретические оценки временной и емкостной алгоритмической сложности одного запуска ГА.
- Проанализируйте результаты ГА для минимизации ДИ на случайных данных (табл. 30.1). Зависит ли доля сокращаемой ДИ от ее объема?
- Выполните задание, аналогичное сформулированному в упражнении 2, для задачи оптимизации ДИ.
- Проанализируйте динамику нахождения решения задачи минимизации ДИ для набора схем из каталога ISCAS-89. Какие выводы можно сделать о числе поколений в процессе эволюции начальной популяции для достижения решения высокого качества?
- Задание, аналогичное предыдущему, выполните для задачи оптимизации ДИ, результаты решения которой представлены в табл. 30.5.
