|
Добрый день можно поинтересоваться где брать литературу предложенную в курсе ?Большинство книг я не могу найти в известных источниках |
Выполнимость булевых функций и бинарные диаграммы в построении тестов
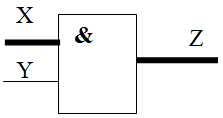
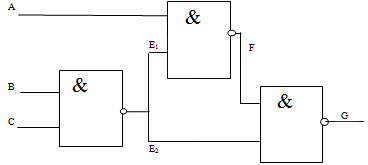
Как отмечалось в предыдущей лекции, где представлен метод SOCRATES, на этапе препроцессорной обработки можно найти нелокальные импликации, которые позволяют сократить число откатов в процессе поиска и тем самым его ускорить. Напомним, что для схемы рис. 19.9 имеет место нелокальная импликация: если 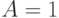 , то отсюда следует
, то отсюда следует 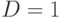 , и наоборот, равенство
, и наоборот, равенство 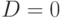 имплицирует
имплицирует  . В соответствии с этим, в КНФ схемы можно явным образом добавить дизъюнкт
. В соответствии с этим, в КНФ схемы можно явным образом добавить дизъюнкт 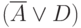 , что в результате дает для схемы следующую КНФ
, что в результате дает для схемы следующую КНФ
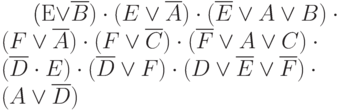
Таким образом, можно дополнительно ввести нелокальные импликации. Однако, на практике они обычно вводятся в случае неудачи с использованием основной КНФ поскольку требуют дополнительных ресурсов.
Кроме этого, можно дополнительно ввести информацию об активизированных путях в схеме, которая используется в структурных методах. Если неисправность обнаружима, то существует, по крайней мере, один активизированный путь между неисправной линией и выходом схемы. Таких путей может быть несколько, но мы выбираем только один активный путь. Каждую линию этого пути назовем активной линией. Для определения активного пути мы для каждого элемента (входящего в путь) дополнительно вводим дизъюнкты, которые для каждой линии этого пути используют вспомогательные переменные. При этом для переменной  вводится активная переменная
вводится активная переменная 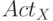 .
Для каждого вентиля с входом
.
Для каждого вентиля с входом  и выходом
и выходом  (входящими в активный путь) мы добавляем дизъюнкт
(входящими в активный путь) мы добавляем дизъюнкт 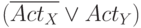 , который показывает, что если активно
, который показывает, что если активно  , то активно
, то активно  . Для элемента, имеющего несколько выходов (например, разветвление) со входом
. Для элемента, имеющего несколько выходов (например, разветвление) со входом  и выходами
и выходами  ,
,  добавляем дизъюнкт
добавляем дизъюнкт 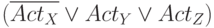 (если активно
(если активно  , то активно
, то активно  или
или  ). На рис. 21.2, 21.3 представлены примеры таких дизъюнктов.
). На рис. 21.2, 21.3 представлены примеры таких дизъюнктов.
Если активно  , то должно быть активно
, то должно быть активно 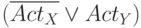 .
.
Если активно  , то должно быть активно
, то должно быть активно 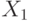 или
или  :
:
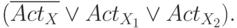
Введение таких дизъюнктов может существенно повысить эффективность системы генерации тестов.
Если вентиль входит в активный путь, то его входы должны иметь неконтролирующие значения, которые позволяют распространять влияние неисправности. Например для вентиля И ни один из неактивных входов не должен иметь значение 0, которое блокирует активизацию. С другой стороны, неактивный вход вентиля И, входящего в активный путь, может также иметь различные сигналы для исправной и неисправной схемы. При этом значения сигналов могут быть согласованы инее согласованы. Эта ситуация показана на рис. 21.4 и рис. 21.5.
На этом основании мы можем добавить дизъюнкты , требующие неконтролирующих значений. Например, для вентиля ИЛИ с активным входом  и неактивным
и неактивным  можно вести дизъюнкт
можно вести дизъюнкт 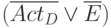 (если
(если  активно, то и
активно, то и  должно быть активно).
Отметим, что учет требования неконтролирующих значений для входов активных элементов в структурных методах имеет очень большое значение, в данном методе это не так, но они позволяют сузить пространство поиска решений.
должно быть активно).
Отметим, что учет требования неконтролирующих значений для входов активных элементов в структурных методах имеет очень большое значение, в данном методе это не так, но они позволяют сузить пространство поиска решений.
Кроме этого, на этапе препроцессорной обработки можно идентифицировать линии уникальной активизации для каждой неисправности и добавить в КНФ активные дизъюнкты для каждого вентиля. Например, для схемы рис. 19.9 аналогично дополнительному дизъюнкту 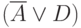 можно генерировать дизъюнкт
можно генерировать дизъюнкт 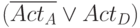 , который показывает, что если
, который показывает, что если  активно, то
активно, то  также должно быть активно.
также должно быть активно.
В некоторых случаях в КНФ можно удалить отдельные переменные, если это не вредит окончательному решению. Будем говорить, что переменная  определяет переменную
определяет переменную  , если присваивание
, если присваивание  значения 0 или 1 ведет к тому, что переменная
значения 0 или 1 ведет к тому, что переменная  везде входит в формулу либо с отрицанием, либо без него.
В этом случае мы можем удалить из формулы все дизъюнкты, содержащие
везде входит в формулу либо с отрицанием, либо без него.
В этом случае мы можем удалить из формулы все дизъюнкты, содержащие  , и отложить присваивание переменной
, и отложить присваивание переменной  до тех пор, пока не будет определено окончательное значение для
до тех пор, пока не будет определено окончательное значение для  . Например, все дизъюнкты, содержащие
. Например, все дизъюнкты, содержащие  ,
, ,
, могут быть удалены из КНФ схемы рис. 21.6.
могут быть удалены из КНФ схемы рис. 21.6.
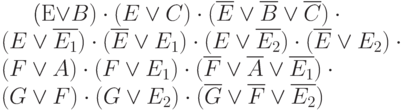
В заключение, отметим, что порядок рассмотрения переменных в процессе решения влияет на его скорость. Поэтому, иногда предварительно определяется порядок рассмотрения переменных, что также способствует улучшению характеристик алгоритма.