Специальные методы сортировки

Параллельная сортировка-слияние

Как сделать так, чтобы несколько независимых процессоров работали совместно над одной задачей сортировки? Управляют ли процессоры внешними запоминающими устройствами или являются самостоятельными вычислительными системами, этот вопрос лежит в основе разработки алгоритмов для высокопроизводительных вычислительных систем. Тема параллельных вычислений в последнее время широко изучается. Разработано множество типов компьютеров с параллельными процессорами, и предложены разнообразные модели параллельных вычислений. Во всех этих случаях задача сортировки выступает как средство проверки эффективности и того, и другого.

Мы уже рассматривали вопросы параллельной обработки данных низкого уровня при изучении сортирующих сетей в разделе 11.2, когда говорили о возможности одновременного выполнения нескольких операций сравнения-обмена. Сейчас мы рассмотрим модель параллельных вычислений высокого уровня с использованием большого количества независимых универсальных процессоров (а не просто компараторов), имеющих доступ к одним и тем же данным. В этом случае мы также игнорируем многие практические аспекты, зато в данном контексте можно исследовать алгоритмические вопросы.

Абстрактная модель, которую мы будем использовать для представления параллельной обработки данных, основана на предположении, что сортируемые файлы распределяются между P независимыми процессорами. Мы полагаем, что имеются

• N записей, подлежащих сортировке;
• P процессоров, способных содержать (N/P) записей.

Присвоим этим процессорам метки 0, 1, ..., P - 1 и будем полагать, что входной файл находится в локальной памяти процессоров (то есть каждый процессор содержит N/P записей). Цель сортировки заключается в переупорядочении записей таким образом, чтобы N/P наименьших записей находились в памяти процессора 0, N/P следующих наименьших записей находились в памяти процессора 1 и так далее, по возрастанию. Как мы увидим далее, существует зависимость между P и общим временем выполнения - и хотелось бы получить количественную оценку этой зависимости, чтобы иметь возможность сравнивать различные стратегии.

Предложенная модель - одна из многих возможных моделей параллельной обработки данных, и для нее так же характерны многие упрощения относительно практического применения, как и для модели внешней сортировки (раздел 11.3). Например, эта модель не учитывает один из наиболее важных вопросов параллельной обработки данных: ограничения на обмен данными между процессорами.

Будем полагать, что стоимость этого обмена данными гораздо выше, чем стоимость обращения к локальной памяти, и что такой обмен наиболее эффективен, если он выполняется последовательно, большими блоками данных. В этом смысле каждый процессор рассматривает память других процессоров как внешние запоминающие устройства. Опять-таки, эта высокоуровневая абстрактная модель может быть неудовлетворительной с практической точки зрения ввиду ее чрезмерной упрощенности; ее также можно считать неудовлетворительной и с теоретической точки зрения, поскольку ей не хватает полноты определения. Но все же она представляет собой основу для разработки полезных алгоритмов.

Данная задача (с учетом сделанных предположений) представляет собой пример мощи абстрактного подхода, поскольку для ее решения можно воспользоваться сортирующими сетями, рассмотренными в разделе 11.2 - нужно лишь внести соответствующие изменения в абстракцию сортировки-слияния, которые сделают ее пригодной для работы с большими блоками данных.

Эту операцию нетрудно реализовать: достаточно слить два входных файла и передать на выход первую и вторую половину полученного файла.

Будем называть метод, описываемый в свойстве 11.7, поблочной сортировкой (block sorting). Прежде чем использовать этот метод на конкретной машине с параллельными процессорами, необходимо рассмотреть значения некоторых параметров. Нам будет интересна следующая характеристика производительности этого метода:

Рис. 11.18. Пример поблочной сортировки

На этом рисунке показано, как можно воспользоваться сетью, представленной на рис. 11.4, для сортировки блоков данных. Компараторы выводят меньшие элементы из двух входных линий на верхнюю линию, а большие элементы - на нижнюю линию. Достаточно трех параллельных шагов.

Для реализации сливающего компаратора на двух процессорах нужно, чтобы они могли обмениваться копиями их блоков данных, выполнять слияние (параллельно), и хранить половины наборов ключей: с меньшими значениями и с большими значениями. Если пересылка блоков происходит медленно по сравнению с быстродействием самих процессоров, то общее время, необходимое для сортировки, можно оценить, умножив время пересылки одного блока на (lgP)2/ 2. Эта оценка предполагает большое число допущений - например, предполагается, что пересылки блоков данных могут производиться параллельно без дополнительных затрат, что редко наблюдается в реальных компьютерах с параллельными процессорами. И все же она представляет собой отправную точку для понимания того, чего можно ожидать от практической реализации.

Если стоимость пересылки блока данных сравнима с быстродействием отдельного процессора (еще одна идеальная цель, к которой реальные машины лишь приближаются), то тогда нужно принимать в расчет время на начальную сортировку. Каждый процессор для начальной сортировки N/P блоков выполняет (N/P) lg (N/P) сравнений (параллельно), и затем примерно P2(lg P) / 2 этапов слияния N/P-и-N/P. Если стоимость сравнения равна , а стоимость слияния на одну запись равна 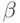, то общее время выполнения приблизительно равно .

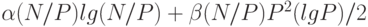Для очень больших N и малых P эта производительность является лучшей из того, на что можно рассчитывать, если использовать метод параллельной сортировки, основанной на сравнениях, поскольку в этом случае затраты равны приблизительно 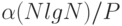, то есть оптимальны: любая сортировка требует N lg N сравнений и лучшее, что можно сделать в этом случае - выполнять P сравнений одновременно. В случае больших значений P преобладает второе слагаемое, и затраты приблизительно равны 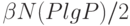, что субоптимально, но вполне конкурентоспособно. Например, при сортировке 1 миллиарда элементов на 64 процессорах вклад второго слагаемого составляет 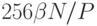, а вклад первого слагаемого - .

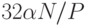При больших значениях P на некоторых машинах могут возникнуть узкие места при передаче данных. В таких случаях для уменьшения издержек может быть использовано идеальное тасование, подобное представленному на рис. 11.8. Именно по этим причинам в некоторых машинах имеются встроенные схемы низкоуровневых соединений, позволяющие эффективно реализовать операции тасования.

Этот пример показывает, что при некоторых условиях можно обеспечить эффективную работу процессоров при сортировке очень больших файлов. Чтобы найти наилучший способ, неизбежно потребуется проанализировать множество различных алгоритмов для данного типа параллельной машины, изучить ее многие другие характеристики и рассмотреть различные модификации. Более того, может потребоваться совершенно другой подход к вопросу параллельной обработки данных. Тем не менее, тот факт, что увеличение количества процессоров приводит к увеличению стоимости обмена данными между ними, является незыблемым для параллельных вычислений, а сети Бэтчера представляют собой эффективное средство управления этими затратами - в этом мы убедились как на низком уровне в разделе 11.2, так и на высоком уровне в настоящем разделе.

Методы сортировки, описанные в этом разделе и в других местах данной главы, отличаются от методов, которые мы изучали в главах 6-10, поскольку здесь приходится учитывать ограничения, которые не рассматриваются в обычном программировании. В главах 6-10 достаточно было простых предположений относительно используемых данных, чтобы можно было сравнивать большое число различных методов решения одной и той же базовой задачи. В противоположность этому в данной главе было сформулировано много различных задач, но для каждой из них было рассмотрено лишь несколько решений. Эти примеры показывают, что изменения ограничений, налагаемых внешней средой, предоставляют возможности для появления новых решений; наиболее важная часть этого процесса состоит в разработке полезных абстрактных формулировок рассматриваемых задач.

Сортировка играет исключительно важную роль во многих практических приложениях, и разработка эффективных методов сортировки часто является одной из первых задач, решаемых на новых компьютерных архитектурах и в новых средах программирования. Учитывая то, что новые разработки строятся на старом опыте, важно иметь представление о наборе технических средств, рассмотренных в главах 6-10; а учитывая то, что появляются совершенно новые подходы, тот способ абстрактного мышления, который был здесь рассмотрен, может пригодиться при разработке быстродействующих процедур сортировки для новых машин.

Упражнения

11.61. Докажите лемму 11.7, воспользовавшись принципом нулей и единиц (лемма 11.1).

11.62. Реализуйте последовательную версию поблочной сортировки с нечетно-четным слиянием Бэтчера: (1) для сортировки блоков данных используйте стандартную сортировку слиянием (программы 8.3 и 8.2), (2) для реализации сливающих компараторов используйте стандартное абстрактное обменное слияние (программа 8.2), а (3) для реализации поблочной сортировки используйте восходящее нечетно-четное слияние Бэтчера (программа 11.3).

11.63. Оцените время выполнения программы, описанной в упражнении 11.62, как функции от N и M, для больших N.

11.64. Выполните упражнения 11.62 и 11.63, но в обоих случаях замените восходящее нечетно-четное слияние Бэтчера (программа 11.3) на программу 8.2.

11.65. Приведите значения P, для которых (N/P) lg N = NP lgP, для N = 10³, 10⁶, 10⁹ и 10¹² .

11.66. Приведите приближенные выражения вида для количества сравнений элементов данных, используемых параллельной поблочной сортировкой Бэтчера для P = 1, 4, 16, 64 и 256.

11.67. Сколько параллельных шагов потребуется для сортировки 10¹⁵ записей, распределенных на 1000 дисках, с помощью 100 процессоров?