Орграфы и DAG-графы

Если учитывать порядок, в котором задаются две вершины каждого ребра графа, получится совершенно другой комбинаторный объект — ориентированный граф (directed graph), или орграф (digraph). Пример орграфа приведен на рис. 19.1. В орграфах обозначение s-t описывает ребро, ведущее из вершины s в вершину t, но оно не дает никакой информации о том, существует ли ребро, ведущее из t в s. Любые две вершины орграфа могут быть связаны одним из четырех видов отношений: ребер между ними нет; имеется ребро s-t, ведущее из s в t; имеется ребро t-s, ведущее из t в s; и имеются два ребра s-t и t-s, которые означают связь в обоих направлениях. Требование однонаправленности естественно для многих приложений, оно легко реализуется и на вид вполне безобидно. Однако оно означает неявное наличие дополнительной комбинаторной структуры, которая существенно влияет на наши алгоритмы и делает работу с орграфами весьма непохожей на работу с неориентированными графами. Обработка орграфов похожа на езду по городу, в котором все улицы имеют одностороннее движение, а направление движения не задается каким-то общим принципом. Можно себе представить, с какими трудностями можно столкнуться в таком городе, если понадобится проехать из одной его точки в другую.

Рис. 19.1.

Ориентированный граф (орграф)

Орграф определяется списком узлов и ребер (внизу), где каждое ребро направлено из первой вершины во вторую. На чертежах орграфа для изображения ориенти-рованныхребер используются стрелки (вверху).

Направления ребер в графе можно интерпретировать различными способами. Например, в графе телефонных вызовов ребро может быть направлено от вызывающего абонента к вызываемому. В бухгалтерских транзакциях ребро может представлять собой денежные суммы, товары или информацию, передаваемые из одного места в другое.

Более современный пример для этой классической модели — интернет, где вершины представляют веб-страницы, а ребра — ссылки между страницами. В разделе 19.4 мы рассмотрим другие примеры для более абстрактных ситуаций.

Довольно часто направление ребер выражает отношение предшествования. Например, орграф может моделировать производственную линию: вершины обозначают этапы выполняемой работы, а ребро из вершины s в вершину t означает, что этап, соответствующий вершине s, должен быть выполнен до выполнения этапа, соответствующего вершине t. Другой способ моделирования той же ситуации заключается в использовании диаграммы PERT (Project Evaluation and Review Technique — сетевое планирование и управление): здесь уже ребра представляют этапы работы, а вершины неявно задают отношение предшествования (все работы, сходящиеся в конкретной вершине, должны быть завершены до начала работ, исходящих из этой вершины). Как узнать, когда нужно приступать к выполнению каждого из этих этапов, чтобы не нарушить ни одно из отношений предшествования? Это так называемая задача составления расписания (scheduling problem). Она не имеет смысла, если в орграфе имеется цикл, и в таких ситуациях мы работаем с DAG-графами (directed acyclic graph — ориентированный ациклический граф). В разделах 19.5—19.7 мы рассмотрим основные свойства DAG-графов и алгоритмы решения простой задачи составления расписания — топологической сортировки (topological sorting). На практике в задачах составления расписаний обычно учитываются веса вершин или ребер, которые моделируют время или стоимость выполнения каждого этапа. Такие задачи будут изучаться в "Кратчайшие пути" и "Потоки в сетях" .

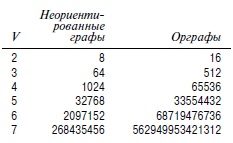
Число возможных орграфов поистине огромно. Каждое из возможных V² ориентированных ребер (считая и петли) может присутствовать или отсутствовать — таким образом, общее количество разных орграфов равно 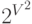. С увеличением количества вершин это число стремительно возрастает (см. рис. 19.2) уже при небольших значениях V, даже по сравнению с количеством различных неориентированных графов. Как и в случае неориентированных графов, количество изоморфных друг другу графов (вершины одного из изоморфных графов можно переименовать таким образом, чтобы получить другой) намного меньше, однако воспользоваться этим сокращением невозможно, т.к. нам неизвестен эффективный алгоритм выявления изоморфизма графов.

Рис. 19.2. Подсчет количества графов

Количество различных неориентированных графов с Vвершинами огромно, даже при малых значениях V, но количество различных орграфов с Vвершинами гораздо больше. Количество неориентированных определяется формулой 2^V(V+1)/2, а количество орграфов — формулой 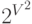2v2.

Разумеется, любая программа обрабатывает лишь мизерную часть возможных орграфов; эти числа так велики, что практически наверняка ни один конкретный орграф не окажется в числе обработанных любой заданной программой. В общем случае трудно как-то охарактеризовать орграфы, с которыми приходится сталкиваться на практике, поэтому приходится разрабатывать алгоритмы так, чтобы они могли справиться с любым заданным орграфом. С одной стороны, мы уже сталкивались с подобными ситуациями (например, ни одна программа сортировки не обрабатывала все 1000! перестановок 1000 элементов). С другой стороны, совсем не воодушевляет тот факт, что, например, даже если все электроны вселенной были бы суперкомпьютерами, способными обрабатывать 10¹⁰ графов за секунду в течение всей жизни Вселенной, то эти суперкомпьютеры не просмотрят и 10^-100 процента орграфов, состоящих из 10 вершин (см. упражнение 19.9).

Это небольшое отступление про подсчет графов выделяет несколько моментов, которым мы уделяем особое внимание, когда проводим анализ алгоритмов, и показывает их непосредственное отношение к изучению орграфов. Стоит ли разрабатывать алгоритмы так, чтобы они хорошо работали в худшем случае, если встретить такой орграф практически невозможно? Есть ли смысл выбирать алгоритмы на основе анализа работы в среднем, или все это чисто математические выкрутасы? Если нам нужно получить программную реализацию, которая эффективно работает на реально встречающихся орграфах, то тогда возникает проблема описания таких орграфов. Разработка математических моделей, достаточно точно описывающих реальные орграфы, является еще более трудным делом, чем для неориентированных графов.

В этой главе мы еще раз рассмотрим подмножество фундаментальных задач обработки графов, которые были исследованы в "Виды графов и их свойства" , но уже в контексте орграфов, а также несколько задач, характерных только для орграфов. А именно, мы рассмотрим поиск в глубину и его применения: обнаружение циклов (является ли данный граф DAG-графом), задача топологической сортировки (например, для решения задачи составления расписаний для DAG-графов), а также вычисление транзитивных замыканий и сильных компонентов (которые решают фундаментальную задачу поиска ориентированного пути между двумя заданными вершинами). Как и в других областях обработки графов, сложность этих алгоритмов может быть любой — от тривиальных до исключительно хитроумных. Они основываются на сложных комбинаторных структурах орграфов и одновременно помогают изучать эти структуры.

Упражнения

19.1. Найдите в интернете пример крупного орграфа — возможно, графа транзакций в какой-то онлайновой системе или орграфа, определяемого ссылками веб-страниц.

19.2. Найдите в интернете пример крупного DAG-графа — возможно, графа определения функций в крупной программной системе или ссылок в каталоге крупной файловой системы.

19.3. Постройте таблицу, аналогичную представленной на рис. 19.2, но без учета графов и орграфов с петлями.

19.4. Каково количество орграфов, содержащих V вершин и E ребер?

19.5. Сколько орграфов соответствует каждому неориентированному графу, содержащему V вершин и E ребер?

19.6. Сколько цифр содержит десятичное число, равное количеству орграфов с V вершинами и E ребрами?

19.7. Начертите неизоморфные орграфы, содержащие три вершины.

19.8. Каково количество различных орграфов, содержащих V вершин и E ребер, если считать орграфы различными только если они не изоморфны.

19.9. Вычислите верхнюю границу процентного отношения орграфов, содержащих 10 вершин, которые могут быть просмотрены каким-либо компьютером в условиях, описанных в тексте, и с учетом того, что во вселенной имеется менее 10⁸⁰ электронов, а возраст Вселенной не превышает 10²⁰ лет.

Глоссарий и правила игры

Наши определения орграфов (как и некоторые используемые нами алгоритмы и программы) почти идентичны определениям неориентированных графов из "Виды графов и их свойства" , однако мы все же приведем их полностью. Небольшие различия в формулировках, касающиеся направлений ребер, влекут появление структурных свойств, которые и будут исследоваться в данной главе.

Как и в случае неориентированных графов, в этом определении исключается наличие одинаковых ребер, но мы будем допускать их в различных приложениях и реализациях, если так будет удобнее. Мы явно разрешаем присутствие петель в орграфах (и обычно допускаем, что такая петля имеется у каждой вершины), поскольку они играют важную роль в фундаментальных алгоритмах.

Мы считаем, что каждая вершина достижима сама из себя, и обычно реализуем это свойство, включая в представление орграфов петли.

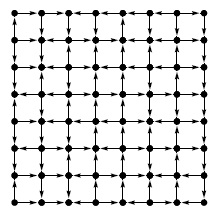
Для понимания многих алгоритмов, описываемых в данной главе, требуется понимание свойств связности орграфов и влияния этих свойств на базовый процесс перемещения от одной вершины к другой по ребрам графа. Достичь такого понимания для орграфов сложнее, чем для неориентированных графов. Например, иногда с первого взгляда видно, является ли небольшой неориентированный граф связным или содержит ли он циклы, однако в орграфах эти свойства не так очевидны, что демонстрирует типичный пример на рис. 19.3.

Конечно, подобные примеры подчеркивают различия, однако важно помнить, что задача, трудная для человека, может быть, а может и не быть трудной для программы — к примеру, написание класса DFS, предназначенного для поиска циклов в орграфе, не труднее задачи поиска циклов в неориентированном графе. И все же орграфы и неориентированные графы во многом существенно различаются. Например, то, что в каком-то орграфе вершина t достижима из вершины s, ничего не говорит о том, достижима ли s из t. Это различие очевидно, но, как мы увидим, весьма существенно.

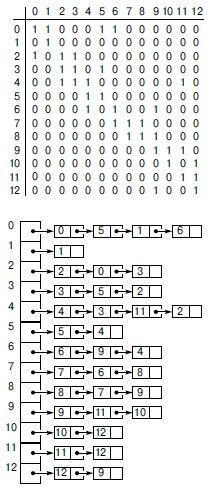
Как было сказано в "Виды графов и их свойства" , представления, используемые для орграфов, по существу те же, что и представления, используемые для неориентированных графов. Вообще-то они даже более наглядны, поскольку каждое ребро в них представлено только один раз — см. рис. 19.4. В представлении списками смежности ребро s-t представляется узлом, содержащим t в связном списке, который соответствует вершине s.

Рис. 19.3. Решетчатый орграф

Этот небольшой орграф похож на крупную решетчатую сеть, которая была рассмотрена в "Введение" — только теперь на каждой линии сетки имеется ориентированное ребро случайно выбранного направления. Даже для такого графа с небольшим количеством вершин его свойства связности совсем не очевидны. Существует ли ориентированный путь из верхнего левого угла в нижний правый?

В представлении матрицей смежности приходится использовать полную матрицу размером V х V, и ребро представляется в ней единицей на пересечении строки s и столбца t. Единицы на пересечении строки t и столбца s нет, если в графе нет ребра t-s. В общем случае матрица смежности для орграфа не симметрична относительно главной диагонали.

В этих представлениях нет различий между неориентированными графами и ориентированными графами с петлей в каждой вершине и двумя ориентированными ребрами для каждого ребра, соединяющего разные вершины неориентированного графа (по одному в каждом направлении). Поэтому алгоритмы, которые мы разработаем в этой главе для орграфов, можно использовать и для обработки неориентированных графов — естественно, при соответствующей интерпретации результатов. Кроме того, в качестве основы для программ обработки орграфов мы будем использовать некоторые программы из "Виды графов и их свойства" : программы 17.7—17.10, реализующие классы DenseGRAPH и SparseMultiGRAPH, строят орграфы, если конструктору передается во втором аргументе значение true.

Рис. 19.4. Представления орграфа

В представлениях орграфа матрицей смежности и списками смежности каждое ребро фигурирует только один раз, как видно из представления орграфа, показанного на рис. 19.1, в виде матрицы смежности (сверху) и в виде списков смежности (внизу). Оба эти представления содержат в каждой вершине петли, которые обычно используются при обработке орграфов.

Степень захода (indegree) вершины орграфа есть количество ориентированных ребер, которые ведут в эту вершину. Степень выхода (outdegree) вершины орграфа есть количество ориентированных ребер, которые ведут из этой вершины. Никакая вершина орграфа не достижима из вершины со степенью выхода 0 — такая вершина называется сток (sink); вершина со степенью захода 0 называется исток (source), она не достижима ни из какой вершины орграфа. Орграф, в котором разрешены петли, и степень выхода каждой вершины равна 1, называется отображением (map) (функция из множества целых чисел от 0 доV— 1 на это же множество). Используя векторы, индексированные именами вершин, можно подсчитать степени захода и выхода для каждой вершины и найти истоки и стоки, потратив на это линейное время и объем памяти, пропорциональный V (см. упражнение 19.19).

Обращение (reverse) орграфа — это орграф, который получается при изменении направлений всех ребер орграфа на обратные. На рис. 19.5 показано обращение орграфа с рис. 19.1 и его представления. Обращения орграфов используются в алгоритмах тогда, когда нужно знать, откуда исходят ребра, поскольку стандартные представления показывают нам только куда они идут. При обращении орграфа степени выхода и захода меняются местами.

В случае представления матрицей смежности обращение можно вычислить, создав копию матрицы и транспонировав ее (поменяв местами строки и столбцы).

Рис. 19.5. Обращение орграфа

Изменение направлений ребер орграфа на обратные соответствует транспонированию матрицы смежности, но требует перестроения списков смежности (см. рис. 19.1 и рис. 19.4).

Если известно, что граф в дальнейшем не будет изменяться, то можно использовать его обращение без каких-либо дополнительных вычислений — просто переставляя вершины в обращениях к ребрам при работе с обращенным графом. Например, ребро s-t орграфа G задано значением 1 в элементе adj[s][t]. Значит, если бы мы вычислили обращение R орграфа G, оно содержало бы 1 в элементе adj[t][s]. Но ведь это можно и не делать: если в реализации клиента выполняется проверка ребра edge(s,t), то для работы с обращением достаточно заменить каждую такую ссылку на edge(t,s). Несмотря на очевидность, этой возможностью часто пренебрегают. Однако в случае представления списками смежности обращение представляет собой совершенно другую структуру данных, и, как видно из программы 19.1, для ее построения нужно время, пропорциональное количеству ребер орграфа.

Еще один способ, который будет применяться в "Потоки в сетях" — использование двух представлений каждого ребра, как в случае неориентированных графов (см. "Виды графов и их свойства" ), но с дополнительным битом, указывающим направление ребра. Например, в представлении орграфа списками смежности ребро s-t будет представлено узлом t в списке смежности вершины s (бит направления указывает прямой проход по ребру из s в t) и узлом s в списке смежности вершины t (бит направления указывает обратный проход по ребру из t в s). Такое представление поддерживает алгоритмы, где необходимы проходы по ребрам орграфа в обоих направлениях. В таких случаях обычно удобно добавлять указатели, соединяющие оба представления ребра. Мы отложим подробное исследование такого представления до "Потоки в сетях" , где оно играет существенную роль.