Слияние и сортировка слиянием

Семейство алгоритмов быстрой сортировки, рассмотренное в "Быстрая сортировка" , основано на операции выборки, т.е. на нахождении k-го минимального элемента в файле. Мы убедились в том, что выполнение операции выборки аналогично делению файла на две части: часть, содержащую к меньших элементов, и часть, содержащую N- k больших элементов. В этой главе мы рассмотрим семейство алгоритмов сортировки, основанных на противоположном процессе, слиянии, т.е. объединении двух отсортированных файлов в один файл большего размера. На слиянии основан простой алгоритм сортировки вида "разделяй и властвуй" (см. "Рекурсия и деревья" ), а также его двойник - алгоритм восходящей сортировки слиянием, при этом оба алгоритма достаточно просто реализуются.

Выборка и слияние - противоположные операции в том смысле, что выборка разбивает файл на два независимых файла, а слияние объединяет два независимых файла в один. Контраст между этими двумя операциями становится очевидным при применении принципа " разделяй и властвуй " для создания конкретных методов сортировки. Можно переупорядочить файл таким образом, что если отсортировать обе части файла, становится упорядоченным и весь файл; и наоборот, можно разбить файл на две части, отсортировать их, а затем объединить упорядоченные части и получить весь файл в упорядоченном виде. Мы уже видели, что получается в первом случае: это быстрая сортировка, состоящая из процедуры выборки, за которой следуют два рекурсивных вызова. В этой главе мы рассмотрим сортировку слиянием (mergesort), которая является противоположностью быстрой сортировки, поскольку состоит из двух рекурсивных вызовов с последующей процедурой слияния.

Одним из наиболее привлекательных свойств сортировки слиянием является тот факт, что она сортирует файл, состоящий из N элементов, за время, пропорциональное N logN, независимо от характера входных данных. В "Очереди с приоритетами и пирамидальная сортировка" мы познакомимся с еще одним алгоритмом, время выполнения которого гарантированно пропорционально NlogN; этот алгоритм носит название пирамидальной сортировки (heapsort). Основной недостаток сортировки слиянием заключается в том, что простые реализации этого алгоритма требуют объема дополнительной памяти, пропорционального N. Это препятствие можно преодолеть, однако способы сделать это настолько сложны, что практически неприменимы, особенно если учесть, что можно воспользоваться пирамидальной сортировкой. Кодирование сортировки слиянием не труднее кодирования пирамидальной сортировки, а длина ее внутреннего цикла находится между аналогичными показателями быстрой сортировки и пирамидальной сортировки; так что сортировка методом слияния достойна внимания, если важно быстродействие, недопустимо ухудшение производительности на " неудобных " входных данных и доступна дополнительная память.

Гарантированное время выполнения, пропорциональное NlogN, может быть и недостатком. Например, в "Элементарные методы сортировки" были описаны методы, которые могут быть адаптированы таким образом, что в некоторых особых ситуациях время их выполнения может быть линейным - например, при достаточно высокой упорядоченности файла либо при наличии лишь нескольких различных ключей. В противоположность этому время выполнения сортировки слиянием зависит главным образом от числа ключей входного файла и практически не чувствительно к их упорядоченности.

Сортировка слиянием является устойчивой, и это склоняет чашу весов в ее пользу в тех приложениях, в которых устойчивость важна. Конкурирующие с ней методы, такие как быстрая сортировка или пирамидальная сортировка, не относятся к числу устойчивых. Различные приемы, обеспечивающие устойчивость этих методов, обычно требуют дополнительной памяти; поэтому если на первый план выдвигается устойчивость, то требование дополнительной памяти для сортировки слиянием становится менее важным.

У сортировки слиянием есть еще одно, иногда очень важное, свойство: она обычно реализуется таким образом, что обращается к данным в основном последовательно (один элемент за другим). Поэтому сортировка слиянием удобна для упорядочения связных списков, для которых применим только метод последовательного доступа. По тем же причинам, как мы увидим в "Специальные методы сортировки" , на слиянии часто основываются методы сортировки для специализированных и высокопроизводительных машин, поскольку в таких вычислительных средах последовательный доступ к данным является самым быстрым.

Двухпутевое слияние

При наличии двух упорядоченных входных файлов их можно объединить в один упорядоченный выходной файл, просто повторяя цикл, в котором меньший из двух элементов, наименьших в своих файлах, переносится в выходной файл; и так до исчерпания обоих входных файлов. В этом и следующем разделах будут рассмотрены несколько реализаций этой базовой абстрактной операции. Время выполнения линейно зависит от количества элементов в выходном файле, если на каждую операцию поиска следующего наименьшего элемента в любом входном файле затрачивается постоянное время, а это верно, если отсортированные файлы представлены структурой данных, поддерживающей последовательный доступ за постоянное время, наподобие связного списка или массива. Эта процедура представляет собой двухпутевое слияние (two-way merging); в "Специальные методы сортировки" мы подробно изучим многопутевое слияние, в котором принимают участие более двух файлов. Наиболее важным приложением многопутевого слияния является внешняя сортировка, которая подробно рассматривается там же.

Для начала предположим, что имеются два отдельных упорядоченных массива целых чисел a[0], ..., a[N-1] и b[0], ..., b[M-1], которые нужно объединить в третий массив c[0], ..., c[N+M-1]. Легко реализуемая очевидная стратегия заключается в том, чтобы последовательно выбирать в с наименьший элемент из оставшихся в a и b, как показано в программе 8.1. Эта простая реализация обладает двумя важными характеристиками, которые мы сейчас рассмотрим.

Во-первых, в данной реализации предполагается, что массивы не пересекаются. В частности, если a и b - большие массивы, то для размещения выходных данных необходим третий, тоже большой, массив c. Было бы хорошо не задействовать дополнительную память, пропорциональную размеру выходного файла, а применить такой метод,

Программа 8.1. Слияние

Чтобы объединить два упорядоченных массива a и b в упорядоченный массив c, используется цикл for, который на каждой итерации помещает в массив c очередной элемент. Если массив a исчерпан, элемент берется из b; если исчерпан b, то элемент берется из a; если же элементы есть и в том, и в другом массиве, то в c переносится наименьший из оставшихся элементов в a и b. Предполагается, что оба входных массива упорядочены, и что массив c не пересекается (т.е. не перекрывает и не использует совместную память) с массивами a и b.

template <class Item>
void mergeAB(Item c[], Item a[], int N, Item b[], int M )
  { for (int i = 0, j = 0, k = 0; k < N+M; k++)
     {
       if (i == N) { c[k] = b[j++]; continue; }
       if (j == M) { c[k] = a[i++]; continue; }
       c[k] = (a[i] < b[j]) ? a[i++] : b[j + +];
    }
  }
        

который объединяет два упорядоченных файла a[1], ..., a[m] и a[m+1], ..., a[r] в один упорядоченный файл, просто перемещая элементы a[1], ..., a[r] без использования существенного объема дополнительной памяти. Здесь стоит остановиться и подумать о том, как это можно сделать. На первый взгляд кажется, что эту задачу решить просто, однако на самом деле все известные до сих пор решения достаточно сложны, особенно по сравнению с программой 8.1. Оказывается, довольно трудно разработать алгоритм обменного (т.е. на том же месте) слияния, который обошел бы по производительности альтернативные обменные сортировки. Мы еще вернемся к этому вопросу в разделе 8.2.

Слияние, как операция, имеет свою собственную область применения. Например, в типичной среде обработки данных может оказаться нужным использовать большой (упорядоченный) файл данных, в который регулярно добавляются новые элементы. Один из подходов заключается в пакетном добавлении новых элементов в главный (намного больший) файл и последующей сортировке всего файла. Однако эта ситуация как будто специально создана для слияния: гораздо эффективнее отсортировать (небольшой) пакет новых элементов и потом слить полученный небольшой файл с большим главным файлом. Слияние используется во многих аналогичных приложениях, так что изучать его, несомненно, стоит. Поэтому основное внимание в данное главе будет уделяться методам сортировки, в основу которых положено слияние.

Упражнения

8.1. Предположим, что упорядоченный файл размером N нужно объединить с неупорядоченным файлом размером M, причем M намного меньше N. Допустим, что у нас имеется программа сортировки, которая упорядочивает файл размером N за с₁ NlgN секунд, и программа слияния, которая может слить файл размером N с файлом размером M за c₂(N + M) секунд, при 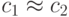. Во сколько раз быстрее, чем сортировка заново, работает предложенный метод, основанный на слиянии, если его рассматривать как функцию от M, при N = 10³, 10⁶ и 10⁹ ?

8.2. Сравните сортировку всего файла методом вставок и два метода, представленные в упражнении 8.1. Считайте, что меньший файл упорядочен случайным образом, так что каждая вставка проходит примерно полпути в большом файле, а время выполнения сортировки имеет порядок c₃ M N/ 2 , при этом константа с₃ примерно равна другим константам.

8.3. Опишите, что произойдет, если попробовать воспользоваться программой 8.1 для обменного слияния с помощью вызова merge(a, a, N/2, a+N/2, N-N/2) для ключей A E Q S U Y E I N O S T.

8.4. Верно ли, что программа 8.1, вызванная так, как описано в упражнении 8.3, дает правильный результат тогда и только тогда, когда оба входных подмассива отсортированы? Обоснуйте свой ответ или приведите контрпример.