Специальные методы сортировки

Методы сортировки являются критическими компонентами многих прикладных систем. Довольно часто предпринимаются специальные меры, чтобы сортировка работала максимально быстро или могла обрабатывать очень большие файлы. Нередко появляются усовершенствования вычислительных систем, или специальные аппаратные средства, повышающие производительность сортировки, или просто новые компьютерные системы, основанные на новых архитектурных решениях. В таких случаях представления об относительной стоимости операций, выполняемых над сортируемыми данными, могут оказаться неверными. В данной главе мы рассмотрим примеры методов сортировки, разработанных для эффективного применения на различных типах машин. Мы рассмотрим некоторые виды ограничений, налагаемых высокопроизводительными аппаратными средствами, а также несколько методов, которые могут оказаться полезными для практической реализации высокоэффективных видов сортировки.

Проблема поддержки эффективных методов сортировки рано или поздно встает перед любой новой компьютерной архитектурой. В самом деле, исторически сложилось так, что сортировка служит своеобразным испытательным полигоном при разработке новой архитектуры, поскольку она и практически важна, и легка для понимания. Хочется знать не только то, какой из известных алгоритмов и в силу каких причин выполняется на новой машине лучше других, но также и то, можно ли при разработке нового алгоритма воспользоваться конструктивными особенностями конкретной машины. Чтобы разработать новый алгоритм, мы определяем некоторую абстрактную машину, инкапсулирующую основные свойства реальной машины, разрабатываем и анализируем алгоритмы для этой абстрактной машины, затем реализуем, тестируем и усовершенствуем как сами алгоритмы, так и модель машины. Конечно, при этом мы опираемся на предыдущий опыт, в том числе и множество методов для машин общего назначения, изложенных в главах 6-10, но ограничения абстрактных машин помогают учесть реальные затраты и убедиться в том, что для разных машин годятся различные алгоритмы.

На одном конце спектра находятся модели низкого уровня, в которых разрешается выполнение только операции сравнения-обмена. На другом конце спектра находятся модели высокого уровня, в которых можно выполнять считывание и запись больших блоков данных на медленные внешние носители или распределять вычисления между независимыми параллельными процессорами.

Сначала мы рассмотрим версию сортировки слиянием, известную как нечетно-четная сортировка слиянием Бэтчера. В ее основу положен алгоритм слияния " разделяй и властвуй " , использующий для перемещения данных только операции сравнения-обмена и операции идеального тасования и идеального обратного тасования. Эти операции представляют интерес и сами по себе, и применяются для решения задач, отличных от сортировки. Далее мы рассмотрим метод Бэтчера в виде сортирующей сети. Сортирующая сеть представляет собой простую абстракцию для аппаратных средств сортировки. Такие сети состоят из соединенных друг с другом компараторов - модулей, способные выполнять операции сравнения-обмена.

Другой важной задачей абстрактной сортировки является задача внешней сортировки - когда сортируемый файл слишком велик, чтобы поместиться в оперативной памяти. Стоимость доступа к отдельным записям может оказаться слишком высокой, поэтому используется абстрактная модель, в которой записи передаются на внешние устройства и обратно в виде блоков больших размеров. Мы рассмотрим два алгоритма внешней сортировки и воспользуемся соответствующей моделью для их сравнения.

И в заключение мы рассмотрим параллельную сортировку, когда сортируемый файл распределяется между независимыми параллельными процессорами. Мы дадим определение простой модели параллельной машины, а затем выясним, при каких условиях метод Бэтчера обеспечит эффективное решение этой задачи. Использование одного и того же базового алгоритма для решения задачи как высокого, так и низкого уровня служит наглядной иллюстрацией мощи применения абстракций.

Различные абстрактные машины, приведенные в этой главе, достаточно просты, однако они заслуживают рассмотрения, поскольку демонстрируют конкретные ограничения, которые могут оказаться критичными для некоторых приложений сортировки. Аппаратные средства сортировки низкого уровня должны состоять из простых компонентов; внешняя сортировка очень больших файлов обычно требует доступа к блокам данных, а параллельная сортировка накладывает ограничения на межпроцессорные связи. С одной стороны, невозможно оценить алгоритм, пользуясь подробной моделью машины, которая не соответствует какой-либо реальной машине; с другой стороны, рассматриваемые нами абстракции приводят не только к теоретическим формулировкам, содержащим информацию о существенных ограничениях, но и к интересным алгоритмам, которые можно использовать непосредственно на практике.

Нечетно-четная сортировка слиянием Бэтчера

Для начала мы рассмотрим метод сортировки, основанный на всего лишь двух абстрактных операциях: операции сравнения-обмена (compare-exchange) и операции идеального тасования (perfect shuffle) вместе с ее антиподом, операцией идеального обратного тасования (perfect unshuffle). Алгоритм, разработанный Бэтчером в 1968 г., известен как нечетно-четная сортировка слиянием Бэтчера (Batcher’s odd-even mergesort). Реализовать алгоритм, используя операции тасования, сравнения-обмена и двойной рекурсии, несложно; гораздо труднее понять, почему алгоритм работает, и распутать все перетасовки и рекурсии, чтобы понять, как он работает на нижнем уровне.

Мы уже мельком встречались с операцией сравнения-обмена в "Элементарные методы сортировки" , где отметили, что некоторые рассматриваемые там элементарные методы сортировки можно более четко выразить в терминах этой абстрактной операции. Теперь же нас интересуют методы, сравнивающие данные исключительно с помощью операций сравнения-обмена. Стандартные операции сравнения исключаются: операции сравнения-обмена не возвращают результат, поэтому у программы нет возможности выполнять те или иные действия в зависимости от значений данных.

В этом разделе мы допускаем использование операций, которые выполняют часть переупорядочивания данных, такие как операции обмена и тасования, но, как мы увидим в разделе 11.2, без этих операций можно обойтись. Неадаптивные методы эквивалентны линейным (straight-line) программам сортировки: они могут быть записаны в виде простого списка выполняемых операций сравнения-обмена. Например, последовательность вызовов

  compexch(a[0], a[1])
  compexch(a[1], a[2])
  compexch(a[0], a[1])
   

является линейной программой сортировки трех элементов. Для удобства и компактной записи алгоритма используются циклы, тасования и другие операции высокого уровня, однако основная цель при разработке алгоритма состоит в том, чтобы для каждого N определить фиксированную последовательность операций compexch, которая способна выполнить сортировку любого набора из N ключей. Без потери общности можно предположить, что ключи принимают целочисленные значения от 1 до N (см. упражнение 11.4). Чтобы убедиться в том, что линейная программа работает правильно, необходимо доказать, что она сортирует каждую из возможных перестановок этих значений (см., например, упражнение 11.5).

Рис. 11.1. Идеальное тасование и идеальное обратное тасование

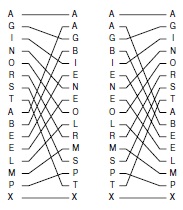
Для выполнения идеального тасования (слева) берется первый элемент файла, затем первый элемент из второй половины файла, затем второй элемент файла, второй элемент из второй половины файла и т.д. Если перенумеровать элементы сверху вниз, начиная с 0, то элементы из первой половины попадут в четные позиции, а элементы из второй половины - в нечетные позиции. Для выполнения идеального обратного тасования (справа) выполняется обратная процедура: элементы из четных позиций попадают в первую половину файла, а элементы из нечетных позиций - во вторую половину.

Лишь немногие из алгоритмов, рассмотренных в главах 6-10, являются неадаптивными: все они используют операцию <, либо как-то по-другому анализируют ключи, после чего выполняют действия в зависимости от значений ключей. Одним из исключений является пузырьковая сортировка (см. "Элементарные методы сортировки" ), использующая только операции сравнения-обмена. Еще одним примером неадаптивного метода сортировки служит версия Пратта сортировки Шелла (см. "Элементарные методы сортировки" ).

В программе 11.1 приведена реализация других абстрактных операций, которыми мы будем пользоваться в дальнейшем - операции идеального тасования и операции идеального обратного тасования, а на рис. 11.1 приведены примеры каждой из них. Идеальное тасование переупорядочивает массив так, как тасует колоду карт опытный картежник: колода делится точно пополам, затем карты по одной берутся из каждой половины колоды. Первая карта всегда берется из верхней половины колоды. Если число карт в колоде четное, в обеих половинах содержится одинаковое их число, если число карт нечетное, то лишняя карта будет последней в верхней половине колоды.

Программа 11.1. Идеальное тасование и идеальное обратное тасование

Функция shuffle переупорядочивает подмассив a[l], ..., a[r] с помощью деления этого подмассива пополам и чередования элементов из каждой половины массива: элементы из первой половины заносятся в четные позиции результирующего массива, а элементы из второй половины - в нечетные позиции. Функция unshuffle выполняет обратное действие: элементы из четных позиций заносятся в первую половину результирующего массива, а элементы из нечетных позиций - во вторую половину. Мы будем применять эти функции только к подмассивам, содержащим четное число элементов.

  template <class Item>
  void shuffle(Item a[], int l, int r)
 { int i, j, m = (l+r)/2;
   static Item aux[maxN];
   for (i = l, j = 0; i <= r; i += 2, j++)
  { aux[i] = a[l+j]; aux[i+1] = a[m+1+j]; }
   for (i = l; i <= r; i++) a[i] = aux[i];
 }
  template <class Item>
  void unshuffle(Item a[], int l, int r)
 { int i, j, m = (l+r)/2;
   static Item aux[maxN];
   for (i = l, j = 0; i <= r; i += 2, j++)
  { aux[l+j] = a[i]; aux[m+1+j] = a[i+1]; }
   for (i = l; i <= r; i++) a[i] = aux[i];
 }
   

Идеальное обратное тасование выполняет обратную процедуру: карты попеременно откладываются в верхнюю и нижнюю половину колоды.

Сортировка Бэтчера почти точно совпадает с нисходящей сортировкой слиянием из "Слияние и сортировка слиянием" ; различие состоит лишь в том, что вместо одной из адаптивных реализаций слияния из "Слияние и сортировка слиянием" она использует нечетно-четное слияние Бэтчера - неадаптивное нисходящее рекурсивное слияние. Программа 8.3 сама по себе вообще не обращается к данным, а поскольку используется неадаптивное слияние, то и сама сортировка будет неадаптивной.

На протяжении этого раздела и раздела 11.2 неявно предполагается, что количество сортируемых элементов является степенью 2. Поэтому всегда можно использовать выражение " N/2 " , не опасаясь того, что N - нечетное. Конечно, это предположение практически нереально: рассматриваемые нами программы и примеры работают с файлами любых размеров, однако оно существенно упрощает рассуждения. Мы еще вернемся к этому вопросу в конце раздела 11.2.

Слияние Бэтчера само по себе является рекурсивным методом " разделяй и властвуй " . Для выполнения слияния 1-и-1 нужна только одна операция сравнения-обмена. Во всех прочих случаях, для выполнения слияния N-и-N эта задача сводится обратным тасованием к двум задачам слияния N/2-и-N/2, после рекурсивного решения которых получаются два отсортированных файла. Тасованием этих файлов получается почти отсортированный файл; все, что теперь нужно - это один проход для выполнения N/2 - 1 независимых операций сравнения-обмена между элементами 2i и 2i + 1, для i от 1 до N/2 - 1. Соответствующий пример показан на рис. 11.2. Из этого описания непосредственно следует программа 11.2.