|
Здравствуйте прошла курсы на тему Алгоритмы С++. Но не пришел сертификат и не доступен.Где и как можно его скаачат? |
Специальные методы сортировки
На рис. 11.9 показана еще одна интерпретация рассматриваемого метода, которая вскрывает его базовую структуру.
Начав с двух отсортированных файлов в первом ряду, мы сливаем их с помощью повторения следующей операции:разбиваем каждый ряд на две равные части, чередуем полученные половины (слева) и выполняем операции сравнения-обмена над смежными по вертикали элементами из разных рядов (справа). Сначала было 16 столбцов и 1 ряд, затем 8 столбцов и 2 ряда, 4 столбца и 4 ряда, 2 столбца и 8 рядов и, наконец, 16 рядов и один столбец, который к этому моменту отсортирован.
Сначала мы записываем один файл под другим, далее сравниваем смежные по вертикали элементы и при необходимости выполняем их обмен так, чтобы меньший элемент находился выше большего. Затем мы делим каждый ряд на две равные части и чередуем половины этих рядов, после чего выполняем те же операции сравнения-обмена над данными во второй и третьей строках. В сравнении других пар рядов нет необходимости, поскольку они уже были отсортированы. Операция разбиения-чередования сохраняет упорядочение как рядов, так и столбцов. Эта операция сохраняет упорядоченность и всего файла: каждый шаг удваивает число рядов, сокращает наполовину число столбцов и сохраняет упорядоченность рядов, и в конечном итоге получается один полностью отсортированный столбец из N рядов. Связь между таблицей, представленной на рис. 11.9, и сетью, изображенной в нижней части рис. 11.8, заключается в том, что если развернуть таблицы по столбцам (за элементами первого столбца следуют элементы второго столбца и т.д.) то мы увидим, что преобразование, необходимое для перехода с одного шага на другой, и есть идеальное тасование.
Теперь с помощью абстрактной параллельной машины со встроенными соединениями идеального тасования (см. рис. 11.10) можно непосредственно реализовать сеть, подобную показанной в нижней части рис. 11.8. Такая машина на каждом шаге выполняет, как предписано алгоритмом, операции сравнения-обмена для некоторых пар смежных процессоров, после чего осуществляет идеальное тасование данных. Программирование этой машины сводится к определению, какие пары процессоров должны выполнять операции сравнения-обмена на каждом цикле.
На рис. 11.11 показаны динамические характеристики как восходящего метода, так и версии нечетно-четного слияния Бэтчера с полным тасованием.
Тасование - это важная абстракция, описывающая движение данных в алгоритмах " разделяй и властвуй " , и она возникает в различных задачах, не связанных с сортировкой. Например, если квадратная матрица размером 2n х 2n хранится в памяти по строкам, то n идеальных тасований транспонируют эту матрицу (преобразуют в упорядоченную по столбцам). Более важные примеры - быстрые преобразования Фурье и вычисление полиномов (см. часть 8). Каждая из этих задач может быть решена при помощи циклической машины идеального тасования, подобной показанной на рис. 11.10, но с более мощными процессорами. Можно даже обдумать вариант с использованием универсальных процессоров, способных выполнять прямое и обратное тасование (некоторые из машин этого типа были даже реально построены); к таким параллельным машинам мы еще вернемся в разделе 11.5.
Изображенная на этом рисунке машина с пересекающимися линиями способна эффективно выполнять алгоритм Бэтчера (и множество других). Подобные связи используются в некоторых параллельных компьютерах.
Восходящая версия нечетно-четного слияния (слева) использует последовательность каскадов, которые выполняют операцию сравнения-обмена большой половины одного отсортированного подфайла с меньшей половиной следующего. При добавлении полного тасования (справа) алгоритм выглядит совсем по-другому.
Упражнения
11.16. Приведите примеры сортирующих сетей для четырех (см. упражнение 11.6), пяти и шести элементов, используя минимально возможное количество компараторов.
11.17. Напишите программу для подсчета количества параллельных шагов, необходимых для выполнения любой линейной программы. Совет: Воспользуйтесь следующей стратегией присвоения меток. Пометьте входные линии как принадлежащие к каскаду 0, затем для каждого компаратора выполните следующие действия: пометьте обе выходные линии как входные для каскада i + 1, если метка одной из входных линий равна i, а метка другой линии не больше чем i.
11.18. Сравните время выполнения программы 11.4 с временем выполнения программы 8.3 для случайно упорядоченных ключей при N = 103, 104, 105 и 106.
11.19. Начертите сеть Бэтчера для выполнения слияния 10-и-11.
11.20. Докажите существование зависимости между рекурсивным тасованием и обратным тасованием (см. рис. 11.8).
11.21. Из изложенного в тексте следует, что на рис. 11.7 неявно представлено 11 сетей для упорядочения 21 элемента. Начертите ту из них, которая содержит минимальное количество компараторов.
11.22. Приведите количество компараторов в нечетно-четных сортирующих сетях Бэтчера для  , если при N, не равном степени 2, сети строятся из первых N линий сети, построенной для наименьшей степени 2, большей N.
, если при N, не равном степени 2, сети строятся из первых N линий сети, построенной для наименьшей степени 2, большей N.
11.23. Выведите точное выражение для количества компараторов, используемых в нечетно-четных сетях сортировки Бэтчера при N = 2n . Совет: Сверьте свой ответ с рис. 11.7, на котором показано, что для N, равного 2, 4, 8, 16 и 32, в сетях имеется, соответственно, 1, 3, 9, 25 и 65 компараторов.
11.24. Постройте сортирующую сеть для упорядочения 21 элемента, используя нисходящий рекурсивный стиль, когда сеть размером N строится как композиция сетей размерами 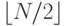 и
и 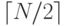 , за которыми следует сливающая сеть. (Для завершающей части сети воспользуйтесь решением упражнения 11.19.)
, за которыми следует сливающая сеть. (Для завершающей части сети воспользуйтесь решением упражнения 11.19.)
11.25. С помощью рекуррентных соотношений подсчитайте количество компараторов в сортирующих сетях, построенных, как описано в упражнении 11.24, для  . Сравните полученные результаты с результатами из упражнения 11.22.
. Сравните полученные результаты с результатами из упражнения 11.22.
11.26. Найдите 16-линейную сортирующую сеть, которая использует меньшее число компараторов, чем сеть Бэтчера.
11.27. Используя схему, описанную в упражнении 11.14, начертите сливающие сети для битонических последовательностей, которые соответствуют рис. 11.8.
11.28. Начертите сортирующие сети, соответствующие сортировке Шелла с последовательностью шагов Пратта ( "Элементарные методы сортировки" ) для N = 32.
11.29. Приведите таблицу, содержащую количество компараторов в сетях, описанных в упражнении 11.28, и количество компараторов в сетях Бэтчера для N = 16, 32, 64, 128 и 256.
11.30. Создайте сортирующие сети, способные выполнять сортировку 3-упорядочен-ных и 4-упорядоченных файлов из N элементов.
11.31. Воспользуйтесь сетями из упражнения 11.30 для разработки схемы, подобной алгоритму Пратта, с использованием множителей 3 и 4. Начертите полученную сеть для N = 32 и решите упражнение 11.29 применительно к этой сети.
11.32. Начертите версию нечетно-четной сортирующей сети Бэтчера для N = 16, в которой между каскадами независимых компараторов, соединяющих смежные линии, выполняются идеальные тасования (четырьмя последними каскадами этой сети должны быть каскады из сети слияния в нижней части рис.11.8).
11.33. Напишите программу слияния для машины, которая изображена на
рис.
11.10, соблюдая следующие соглашения. Каждая инструкция является последовательностью из 15 битов, где i-й бит, при  , показывает (если он равен 1), что процессор i и процессор i - 1 должны выполнить операцию сравнения-обмена. Программа представляет собой последовательность инструкций; между каждыми двумя инструкциями машина выполняет идеальное тасование.
, показывает (если он равен 1), что процессор i и процессор i - 1 должны выполнить операцию сравнения-обмена. Программа представляет собой последовательность инструкций; между каждыми двумя инструкциями машина выполняет идеальное тасование.
11.34. Напишите программу сортировки для машины, изображенной на рис. 11.10, пользуясь соглашениями из упражнения 11.33.



