Поразрядная сортировка

Во многих приложениях сортировки ключи, используемые для упорядочения записей в файлах, могут быть весьма сложными. Представьте, например, насколько сложны ключи, используемые в телефонной книге или в библиотечном каталоге. Чтобы отделить все эти сложности от наиболее важных свойств изучаемых методов сортировки, в главах 6—9 мы почти везде ограничивались использованием только базовых операций сравнения двух ключей и обмена двух записей (скрыв в этих функциях все детали работы с ключами) как абстрактным интерфейсом между методами сортировки и приложениями. В данной главе мы рассмотрим другую абстракцию для ключей сортировки. Например, часто нет необходимости в полной обработке ключей на каждом этапе: при поиске в телефонном справочнике, чтобы найти страницу с номером какого-либо абонента, достаточно проверить лишь несколько первых букв его фамилии. Чтобы добиться такой же эффективности алгоритмов сортировки, мы перейдем от абстрактной операции сравнения ключей к абстракции, в которой ключи разбиваются на последовательность частей фиксированного размера — байтов. Двоичные числа представляют собой последовательности битов, строки — последовательности символов, десятичные числа — последовательности цифр, аналогично могут рассматриваться и многие другие (хотя и не все) типы ключей. Методы сортировки, основанные на обработке ключей по частям, называются поразрядными методами сортировки (radix sort). Эти методы не просто сравнивают ключи, а обрабатывают и сравнивают части ключей.

Алгоритмы поразрядной сортировки интерпретируют ключи как числа, представленные в системе счисления с основанием R, при различных значениях R (основание системы счисления — radix), и работают с отдельными цифрами этих чисел. Например, когда почтово-сортировочная машина обрабатывает пачку конвертов, каждый из которых помечен 5-значным десятичным числом, она распределяет эту пачку на десять отдельных пачек: в одной находятся пакеты, номера которых начинаются с 0, в другой находятся пакеты с номерами, начинающимися с 1, в третьей — с 2 и т.д. Каждая пачка может быть обработана отдельно с помощью того же метода, по следующей цифре, или более простым способом, если в пачке всего лишь несколько пакетов. Если теперь собрать пакеты из пачек в порядке от 0 до 9 и в таком же порядке внутри каждой пачки, то они окажутся упорядоченными. Эта процедура представляет собой поразрядную сортировку с R = 10, и такой метод удобен в приложениях, использующих сортировку, где ключами являются десятичные числа, содержащие от 5 до 10 цифр — наподобие почтовых кодов, телефонных номеров или идентификационных номеров. Этот метод будет подробно рассмотрен в разделе 10.3.

Для различных приложений лучше подходят различные основания системы счисления R. В этой главе мы будем рассматривать в основном ключи, представленные в виде целых чисел или строк, для которых широко применяются методы поразрядной сортировки. Для целых чисел, представляемых в компьютерах в виде двоичных чисел, мы чаще будем работать с R = 2 или с одной из степеней 2, поскольку это позволяет разбивать ключи на независимые части. Для ключей, содержащих строки символов, мы используем R = 128 или R = 256, чтобы согласовать основание системы счисления с размером байта. Вообще-то, помимо таких прямых применений, в виде двоичных чисел можно рассматривать практически все, что записано в компьютере. Это позволяет переориентировать многие приложения сортировки, которые используют другие типы ключей, на использование поразрядной сортировки, которая упорядочивает ключи, представленные в виде двоичных чисел.

Алгоритмы поразрядной сортировки основаны на абстрактной операции " извлечь i-ю цифру ключа " . К счастью, в С++ есть низкоуровневые операции, позволяющие реализовать такие действия просто и эффективно. Это очень важно, поскольку некоторые языки программирования (например, Pascal), поощряя машинно-независимое программирование, намеренно затрудняют написание программ, зависящих от способа представления чисел в конкретной машине. В таких языках трудно реализовать многие виды битовых операций, удобные для выполнения на большинстве компьютеров. В частности, жертвой этой " прогрессивной " философии стала и поразрядная сортировка. Однако создатели С и С++ поняли, что прямые операции с битами часто бывают весьма полезны, и при реализации поразрядной сортировки мы сможем воспользоваться низкоуровневыми языковыми средствами.

Нужна и хорошая аппаратная поддержка; нельзя считать ее само собой разумеющимся фактом. В некоторых машинах имеются эффективные способы доступа к малым порциям данных, но некоторые другие типы машин существенно снижают быстродействие на этих операциях. Поскольку алгоритмы поразрядной сортировки достаточно просто выражаются через операции извлечения разряда числа, задача достижения максимальной производительности алгоритма поразрядной сортировки может оказаться увлекательным введением в аппаратное и программное обеспечение.

Рис. 10.1. Поразрядная сортировка

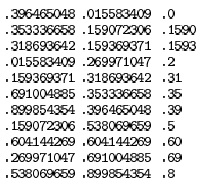
Хотя в данном списке находятся 11 чисел от 0 до 1 (слева), содержащих в совокупности 99 цифр, их можно упорядочить (в центре), проанализировав лишь 22 цифры (справа).

Существуют два принципиально различных базовых подхода к поразрядной сортировке. Первый класс методов составляют алгоритмы, анализирующие цифры в ключах в направлении слева направо, при этом первыми обрабатываются наиболее значащие цифры. Все эти методы вместе называются MSD-сортировками (most significant digit radix sort — поразрядная сортировка сначала по старшей цифре). MSD-сортировки привлекательны тем, что они анализируют минимальный объем информации, необходимый для выполнения сортировки ( рис. 10.1). Методы MSD-сортировки являются обобщением быстрой сортировки, поскольку они разбивают сортируемый файл в соответствии со старшими цифрами ключей, а затем рекурсивно применяют тот же метод к полученным подфайлам. В самом деле, при основании системы счисления, равном 2, реализация MSD-сортировки похожа на быструю сортировку. Во втором классе методов поразрядной сортировки используется другой принцип: они анализируют цифры ключей в направлении справа налево, работая сначала с наименее значащими цифрами. Все эти методы вместе называются LSD-сортировками (least significant digit radix sort — поразрядная сортировка сначала по младшей цифре). LSD-сортировка в какой-то степени противоречит интуиции, поскольку часть процессорного времени затрачивается на обработку цифр, которые не могут повлиять на результат, однако данная проблема легко решается, и этот почтенный метод годится для работы во многих приложениях сортировки.

Биты, байты и слова

Ключом для понимания поразрядной сортировки является осознание того, что (1) компьютеры обычно предназначены для обработки групп битов, называемых машинными словами, которые в свою очередь часто разбиваются на меньшие фрагменты, называемые байтами; (2) ключи сортировки обычно также образуют последовательности байтов; (3) короткие последовательности байтов могут также выступать в качестве индексов массивов или машинных адресов. Поэтому нам будет удобно работать со следующими абстракциями.

В зависимости от контекста ключом в поразрядной сортировке может быть слово или строка. Некоторые из алгоритмов, рассматриваемых в настоящей главе, используют то, что длина ключей фиксирована (слова), другие приспособлены к ситуации, когда ключи имеют переменную длину (строки).

У типичной машины могут быть 8-разрядные байты и 32- и 64-разрядные слова (конкретные значения приведены в заголовочном файле <limits.h>), однако бывает удобно рассматривать и некоторые другие размеры байтов и слов (обычно небольшие кратные или части встроенных машинных размеров). Итак, в качестве числа разрядов в слове и числа разрядов в байте будут использоваться зависящие от архитектуры машины и свойств приложения константы, например:

  const int bitsword = 32;
  const int bitsbyte = 8;
  const int bytesword = bitsword/bitsbyte;
  const int R = 1 << bitsbyte;
      

Для последующего использования, когда мы начнем рассматривать поразрядные сортировки, в эти определения включена также константа R, равная количеству различных значений байта. При использовании таких определений обычно предполагается, что константа bitsword кратна bitsbyte, что число битов в машинном слове не меньше (обычно равно) bitsword, и что каждый байт имеет индивидуальный адрес. В различных компьютерах приняты различные соглашения по обращениям к битам и байтам. Для наших целей мы будем считать, что биты в слове пронумерованы слева направо от 0 до bitsword-1, а байты в слове пронумерованы слева направо от 0 до bytesword-1. В обоих случаях мы полагаем, что нумерация выполняется от наиболее значащих элементов к наименее значащим.

В большинстве компьютеров имеются битовые операции И и сдвиг, которые позволяют извлекать из слов отдельные байты (и биты тоже — прим. перев.).

В C++ можно прямо написать операцию извлечения B-го байта из двоичного слова A следующим образом:

  inline int digit(long A, int B)
    { return (A >> bitsbyte*(bytesword-B-1) & (R-1); }
      

Эта макрокоманда может, например, извлечь байт 2 (третий байт) 32-разрядного числа, сдвинув его вправо на 32 — 3 • 8 = 8 позиций и наложив маску 00000000000000000000000011111111

для обнуления всех разрядов, кроме требуемого байта, который занимает 8 правых разрядов.

Во многих машинах основание системы счисления согласовано с размером байта, что позволяет быстро получить правые биты числа. Эта операция непосредственно поддерживается в С++ для строк в стиле С:

  inline int digit(char* A, int B)
    { return A[B]; }
      

При использовании структуры-оболочки, наподобие рассмотренной в разделе 6.8 "Элементарные методы сортировки" , можно записать:

  inline int digit(Item& A, int B)
    { return A.str[B]; }
      

Этот подход годится и для чисел, хотя различия в представлении чисел могут ограничить переносимость такого кода. В любом случае следует помнить, что в некоторых вычислительных средах подобные операции доступа к отдельным байтам могут быть реализованы с помощью операций сдвига и маскирования, как в предыдущем абзаце.

На несколько другом уровне абстракции можно рассматривать ключи как числа, а байты как цифры. Если дано число (т.е. ключ в виде числа), то для реализации поразрядной сортировки необходима базовая операция извлечения цифры из этого числа. Если в качестве основания системы счисления выбрана степень 2, то цифрами являются группы битов, к которым легко обратиться непосредственно одним из рассмотренных выше методов. Основной причиной использования степени 2 в качестве основания системы счисления как раз и является легкость доступа к группам битов. В некоторых вычислительных средах можно выбирать и другие основания систем счисления. Например, если а — положительное целое число, то b-я цифра числа а в системе счисления R есть .

На машинах, предназначенных для высокопроизводительных численных расчетов, это вычисление может выполняться для произвольного значения R так же быстро, как и для R = 2.

Еще одна точка зрения — рассматривать ключи как числа в диапазоне от 0 до 1, с неявной десятичной точкой слева, как показано на рис. 10.1. В этом случае b-ой цифрой числа a будет .

На машине, эффективно выполняющей эти операции, они позволяют построить поразрядную сортировку. Эта модель применима и в случае ключей переменной длины (строк).

Поэтому в оставшейся части главы мы будем считать ключи числами в системе счисления с основанием R (без указания конкретного значения R) и употреблять абстрактную операцию digit для доступа к отдельным цифрам ключей, считая, что для конкретного компьютера можно разработать быструю реализацию операции digit.

В свете только что рассмотренных примеров вполне можно считать, что эту абстракцию можно эффективно реализовать для многих приложений на большинстве компьютеров — хотя следует соблюдать осторожность, ибо каждая реализация эффективна только в рамках конкретной аппаратной и программной среды.

Мы предполагаем, что ключи достаточно длинные, так что операция извлечения из них битов имеет смысл. Если же ключи короткие, то можно воспользоваться методом распределяющего подсчета из "Элементарные методы сортировки" . Напомним, что этот метод позволяет отсортировать N ключей, представляющие собой целые числа в диапазоне от 0 до R — 1, за линейное время, используя для этой цели одну вспомогательную таблицу размером R для подсчета и другую таблицу, размером N, для переупорядочения записей. Значит, если есть возможность использовать таблицу размером 2w, то сортировку w-разрядных ключей легко выполнить за линейное время. На самом деле метод распределяющего подсчета лежит в основе базовых методов MSD- и LSD-сортировок. Поразрядная сортировка нужна лишь тогда, когда ключи настолько длинны (скажем, w = 64), что использование таблицы размером 2w невозможно.

Упражнения

10.1. Сколько цифр нужно для представления 32-разрядного числа в системе счисления с основанием 256? Опишите, как можно извлечь каждую цифру этого числа. Ответьте на этот же вопрос, если основанием системы счисления будет число 2¹⁶.

10.2. Для N = 10³, 10⁶ и 10⁹ приведите наименьший размер байта, позволяющий представить любое число в диапазоне от 0 до N в виде 4-байтового слова.

10.3. Напишите перегруженную операцию <, используя абстракцию digit (например, чтобы выполнять эмпирические сравнения алгоритмов из глав 6 и 9 с методами, описанными в данной главе, для одних и тех же данных).

10.4. Спроектируйте и проведите эксперимент по сравнению затрат ресурсов на извлечение цифр с помощью операций сдвига и с помощью арифметических операций, реализованных на вашей машине. Сколько цифр вы можете извлечь за секунду, используя каждый из двух этих методов? Примечание: осторожно, ваш компилятор может преобразовать арифметические операции в битовые или наоборот!

10.5. Напишите программу, которая для заданного набора случайных десятичных чисел (R = 10), равномерно распределенных на интервале от 0 до 1, будет вычислять количество операций сравнения цифр, необходимых для их сортировки в смысле рис. 10.1. Выполните эту программу для N = 10³, 10⁴, 10⁵ и 10⁶ .

10.6. Выполните упражнение 10.5 для R = 2, используя случайные 32-разрядные числа.

10.7. Выполните упражнение 10.5 для нормально распределенных чисел (распределение Гаусса).