Минимальные остовные деревья
Модели графов, в которых с каждым ребром связаны веса (weight) или стоимости (cost), используются во многих приложениях. В картах авиалиний, в которых ребрами отмечены авиарейсы, такие веса означают расстояния или стоимости билетов. В электронных схемах, где ребра представляют проводники, веса могут означать длину проводника, его стоимость или время прохода сигнала. В задачах календарного планирования веса могут представлять время или трудоемкость либо выполнения задачи, либо ожидания ее завершения.
В таких ситуациях естественно возникают вопросы, касающиеся минимизации затрат. Мы рассмотрим алгоритмы для двух таких задач: (1) поиск пути наименьшей стоимости, соединяющего все точки, и (2) поиск пути наименьшей стоимости, соединяющего две заданных точки. Первый алгоритм применяется для решения задач на неориентированных графах, которые представляют такие объекты как электрические цепи, и находит минимальное остовное дерево; это дерево является основной темой данной главы. Второй алгоритм применяется для решения задач на орграфах, которые представляют такие объекты, как карты авиарейсов, и определяет кратчайшие пути — он будет темой "Кратчайшие пути" . Эти алгоритмы находят широкое применение не только в приложениях, связанных с электрическими схемами и картами, но и при решении задач на взвешенных графах.
Когда мы изучаем алгоритмы обработки взвешенных графов, то часто интуитивно отождествляем веса с расстояниями, употребляя выражения наподобие " вершина, ближайшая к x ". И термин " кратчайший путь " поддерживает этот способ мышления. Однако, несмотря на многочисленные приложения, которые действительно работают с расстояниями, и несмотря на все преимущества геометрической наглядности для понимания базовых алгоритмов, важно помнить, что веса не обязательно должны быть пропорциональны расстоянию: они могут представлять время, затраты или какую-то другую величину. А в "Кратчайшие пути" мы увидим, что веса в задачах поиска кратчайшего пути могут быть даже отрицательными.
Используя интуитивное понимание при описании алгоритмов и примеров, но все-таки не теряя общности, мы будем использовать неоднозначную терминологию, говоря то о длинах, то о весах. " Короткое " ребро будет означать ребро с низким весом и т.д. В большей части примеров этой главы мы будем использовать веса, пропорциональные расстояниям между вершинами, как на рис. 20.1. Такие графы удобнее в качестве примеров, поскольку в них можно не указывать метки ребер, и все-таки сразу видеть, что более длинные ребра имеют большие веса по сравнению с короткими ребрами.
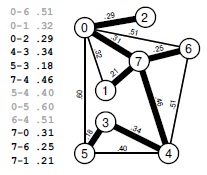
Взвешенный неориентированный граф представляет собой множество взвешенных ребер. MST-дерево есть множество ребер минимального общего веса, которые соединяют все вершины (в списке ребер выделены черным, утолщенные ребра на чертеже). В рассматриваемом графе веса пропорциональны расстояниям между вершинами, однако базовые алгоритмы, которые мы будем изучать, предназначены для обработки графов общего вида и не используют никаких предположений о весах (см. рис. 20.2).
Когда веса представляют расстояния, алгоритмы можно рассматривать c учетом геометрических свойств графов (разделы 20.7 и 21.5). Но вообще-то алгоритмы, которые мы будем изучать, просто обрабатывают ребра, никак не используя неявную геометрическую информацию (см. рис. 20.2).
Задача поиска минимального остовного дерева в произвольном взвешенном неориентированном графе применяется во многих важных ситуациях, и алгоритмы ее решения известны по меньшей мере с двадцатых годов прошлого столетия. Однако эффективности ее реализаций существенно различаются, а исследователи до сих пор пытаются найти более совершенные методы. В этом разделе мы рассмотрим три классических алгоритма, которые легко понять на концептуальном уровне; в разделах 20.3—20.5 мы подробно изучим их реализации, а в разделе 20.6 сравним эти фундаментальные подходы и их основные усовершенствования.
Определение 20.1. Минимальное остовное дерево (minimal spanning tree — MST, другие варианты перевода — минимальный остов, минимальный каркас, минимальный скелет) взвешенного графа есть остовное дерево, вес которого (сумма весов его ребер) не превосходит вес любого другого остовного дерева.
Если все веса положительны, достаточно определить MST-дерево как множество ребер с минимальным общим весом, которые соединяют все вершины, поскольку такое множество как раз образует остовное дерево. Однако условие остовного дерева в определении допускает применение и к графам, в которых ребра могут иметь отрицательные веса (см. упражнение 20.2 и 20.3).
Если ребра могут иметь равные веса, минимальное остовное дерево может не быть единственным. Например, на рис. 20.2 показан граф, который имеет два различных MST-дерева. Возможность равных весов усложняет описание и доказательство правильности некоторых наших алгоритмов. Следует внимательно рассматривать случаи с равными ребрами, т.к. они довольно часто встречаются на практике, а нужно, чтобы наши алгоритмы работали правильно и в таких случаях.
Проблема не только в существовании сразу нескольких MST: это название не отражает достаточно четко то, что минимизируется вес, а не само дерево. Поэтому многие авторы употребляют термин остовное дерево с минимальным весом. Но аббревиатура MST широко распространена и довольно четко отражает базовое понятие.
Однако во избежание путаницы при описании алгоритмов на сетях, в которых могут быть ребра с равными весами, следует аккуратно относиться к терминологии: слово " минимальный " будет обозначать " ребро минимального веса " (среди всех ребер некоторого множества), а " максимальный " — " ребро максимального веса " . То есть если ребра различны, то минимальным ребром является (единственное) самое короткое ребро; но если существует несколько ребер минимального веса, то минимальным может быть любое из них.
В данной главе мы будем работать исключительно с неориентированными графами. Задача поиска ориентированного остового дерева с минимальным весом для орграфов — другая, более трудная задача.
Для решения задачи MST были разработаны несколько классических алгоритмов — как старые и широко известные, так и современные алгоритмы, которые вместе с современными структурами данных позволяют получать компактные и эффективные программные реализации. Такие реализации представляют собой убедительные примеры эффективности тщательного проектирования АТД и правильного выбора фундаментальных структур данных АТД и реализаций алгоритмов для решения все более сложных алгоритмических задач.
В этом примере веса ребер выбраны произвольно и не имеют никакого отношения к геометрии изображенного здесь представления графа. Этот пример также демонстрирует, что MST-дерево не обязательно уникально, если веса ребер могут быть равными: мы получаем одно MST, используя ребро 3-4 (показано на рисунке), и другое MST, используя вместо него 0-5 (хотяребро 7-6 с тем же весом не присутствует ни в одном MST).
Упражнения
20.1. Предположим, что веса в графе положительны. Докажите, что можно изменить их вес, добавив к каждому из них константу или умножив на константу, и при этом MST-деревья не изменятся, если все полученные веса останутся положительными.
20.2. Покажите, что если веса ребер положительны, то множество ребер, соединяющих все вершины, суммарный вес которых не больше суммы весов любого другого множества ребер, соединяющих все эти вершины, составляет MST-дерево.
20.3. Покажите, что свойство, сформулированное в упражнении 20.2, справедливо и для графов с отрицательными весами, в которых нет циклов, все ребра которых имеют неположительные веса.
20.4. Как найти максимальное остовное дерево взвешенного графа?
20.5. Покажите, что если все ребра графа имеют различные веса, то MST-дерево уникально.
20.6. Проанализируйте утверждение, что граф обладает уникальным MST-деревом, только когда веса его ребер различны. Докажите его или приведите контрпример.
20.7. Предположим, что граф имеет t < Vребер с равными весами, а веса всех других ребер различны. Приведите верхнюю и нижнюю границы количества различных MST-деревьев, которые могут быть у графа.