|
Здравствуйте прошла курсы на тему Алгоритмы С++. Но не пришел сертификат и не доступен.Где и как можно его скаачат? |
Минимальные остовные деревья
Сравнения и усовершенствования
Значения времени выполнения рассмотренных базовых алгоритмов вычисления MST приведены в таблице 20.1, а в таблице 20.2 собраны результаты эмпирического сравнения этих алгоритмов. Эти данные показывают, что реализация алгоритма Прима для матрицы смежности лучше подходит для насыщенных графов, что все другие методы отличаются по производительности от наилучшего результата лишь небольшими постоянными множителями (время на извлечение ребер) для графов средней насыщенности, и что метод Крускала сводит задачу к сортировке для разреженных графов.
В общем, для практических целей задачу вычисления MST можно считать " решенной " . Для большинства графов трудоемкость нахождения MST-дерева лишь ненамного превышает затраты на извлечение ребер графа. Это правило не распространяется на крупные очень разреженные графы, но даже и в этом случае производительность может быть повышена примерно в 10 раз по сравнению с лучшими из других известных алгоритмов. Результаты, приведенные в таблице 20.2, зависят от модели, использованной для генерирования графов, хотя они характерны и для многих других моделей (см., например, упражнение 20.80). Однако теоретические результаты не отрицают существования алгоритмов с гарантированным линейным временем выполнения на всех графах. Здесь мы просто ознакомимся с обширными исследованиями по совершенствованию реализаций этих методов.
Здесь приведены значения трудоемкости (в худшем случае) различных алгоритмов вычисления MST-дерева для алгоритмов, рассмотренных в данной главе. Все формулы выведены в предположении, что MST существует (то есть E > V— 1), и имеются Xребер, длина которых не больше длины самого длинного ребра в MST (см. лемму 20.10). Эти граничные значения для худшего случая могут оказаться слишком осторожными для прогнозирования трудоемкости обработки реальных графов. В большом количестве реальных ситуаций время выполнения алгоритмов почти линейно.
| Алгоритм | Затраты в худшем случае | Примечание |
|---|---|---|
| Прима (стандартный) | V2 | Оптимален для насыщенных графов. |
| Прима (PFS, пирамидальное дерево) | E lgV | Осторожная верхняя граница. |
| Прима (PFS, пирамидальное d-дерево) |

|
Линейное время выполнения на всех графах, кроме очень разреженных. |
| Крускала | E lgE | Превалируют затраты на сортировку. |
| Крускала (частичная сортировка) | E + X lgV | Затраты зависят от веса самого длинного ребра. |
| Борувки | E lgE | Осторожная верхняя граница. |
Прежде всего, обширные исследования привели к разработке более совершенных реализаций очереди с приоритетами. Расширение биномиальной очереди — пирамидальное дерево Фибоначчи (Fibonacci heap) — достигает теоретически оптимальной производительности, выполняя операции уменьшить ключ за постоянное время и операции извлечь минимальное за логарифмическое время, что, в соответствие с леммой 20.8, приводит к выполнению алгоритма Прима за время, пропорциональное E + VlgV Пирамидальные деревья Фибоначчи более сложны, чем биномиальные очереди, и не совсем удобны для работы, а некоторые из простых реализации очередей с приоритетами имеют похожие характеристики производительности (см. раздел ссылок).
Один из эффективных подходов — применение поразрядных методов в реализации очереди с приоритетами. По производительности такие методы обычно эквивалентны методу Крускала с поразрядной сортировкой или даже применению поразрядной быстрой сортировки для метода с частичным упорядочением, который был рассмотрен в разделе 20.4.
Одним из наиболее эффективных является другой давно известный простой подход, предложенный Д. Джонсоном (D. Jonhson) в 1977 г.: реализация очереди с приоритетами для алгоритма Прима с помощью d-арных пирамидальных деревьев, а не стандартных бинарных пирамидальных деревьев (см. рис. 20.17).
Здесь приведены относительные значения времени выполнения различных алгоритмов вычисления MST для случайных взвешенных графов разной насыщенности. При малых плотностях лучше работает алгоритм Крускала, поскольку в нем задействована быстрая сортировка. При большой насыщенности лучшей является классическая реализация алгоритма Прима, поскольку в ней нет обработки списков. Для графов средней плотности реализация алгоритма Прима с поиском по приоритету выполняется за время, необходимое для проверки каждого ребра графа, с небольшим постоянным коэффициентом.
| E | V | C | H | J | P | K | K* | e/E | B | e/E |
|---|---|---|---|---|---|---|---|---|---|---|
| Насыщенность 2 | ||||||||||
| 20000 | 10000 | 2 | 22 | 27 | 9 | 11 | 1,00 | 14 | 3,3 | |
| 50000 | 25000 | 8 | 69 | 84 | 24 | 31 | 1,00 | 38 | 3,3 | |
| 100000 | 50000 | 15 | 169 | 203 | 49 | 66 | 1,00 | 89 | 3,8 | |
| 200000 | 100000 | 30 | 389 | 478 | 108 | 142 | 1,00 | 189 | 3,6 | |
| Насыщенность 20 | ||||||||||
| 20000 | 1000 | 2 | 5 | 4 | 20 | 6 | 5 | 0,20 | 9 | 4,2 |
| 50000 | 2500 | 12 | 12 | 13 | 130 | 16 | 15 | 0,28 | 25 | 4,6 |
| 100000 | 5000 | 14 | 27 | 28 | 34 | 31 | 0,30 | 55 | 4,6 | |
| 200000 | 10000 | 29 | 61 | 61 | 73 | 68 | 0,35 | 123 | 5,0 | |
| Насыщенность 100 | ||||||||||
| 100000 | 1000 | 14 | 17 | 17 | 24 | 30 | 19 | 0,06 | 51 | 4,6 |
| 250000 | 2500 | 36 | 44 | 44 | 130 | 81 | 53 | 0,05 | 143 | 5,2 |
| 500000 | 5000 | 73 | 93 | 93 | 181 | 113 | 0,06 | 312 | 5,5 | |
| 1000000 | 10000 | 151 | 204 | 198 | 377 | 218 | 0,06 | 658 | 5,6 | |
| Насыщенность V/2,5 | ||||||||||
| 400000 | 1000 | 61 | 60 | 59 | 20 | 137 | 78 | 0,02 | 188 | 4,5 |
| 2500000 | 2500 | 597 | 409 | 400 | 128 | 1056 | 687 | 0,01 | 1472 | 5,5 |
| Обозначения: | |
| C | Извлекается всего ребер. |
| H | Алгоритм Прима (списки смежности и индексированное пирамидальное дерево). |
| J | Версия Джонсона алгоритма Прима (очередь с приоритетами на основе а-арного пирамидального дерева. |
| P | Алгоритм Прима (представление матрицей смежности). |
| K | Алгоритм Крускала. |
| K* | Версия алгоритма Крускала с частичной сортировкой. |
| B | Алгоритм Борувки. |
| e | Просмотренные ребра (операции объединить). |
Программа 20.10 представляет собой полную реализацию используемого нами интерфейса очереди с приоритетами, которая основана на этом методе. При такой реализации очереди с приоритетами операция уменьшить ключ выполняется менее чем за logdV шагов, а операция извлечь минимальное — за время, пропорциональное  . Тогда, согласно лемме 20.8, время выполнения алгоритма Прима будет пропорционально
. Тогда, согласно лемме 20.8, время выполнения алгоритма Прима будет пропорционально 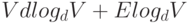 , т.е. линейно для не разреженных графов.
, т.е. линейно для не разреженных графов.
Лемма 20.12. Пусть задан граф с V вершинами и E ребрами, а d означает его насыщенность E/ V. Если d < 2, то время выполнения алгоритма Прима пропорционально VlgV. Иначе можно уменьшить время выполнения в худшем случае в lg(E/V) раз, используя очередь с приоритетами на основе  -арного пирамидального дерева.
-арного пирамидального дерева.
Доказательство. Продолжая рассуждения из предыдущего абзаца, получим, что количество шагов равно 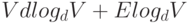 , поэтому время выполнения не более чем пропорционально
, поэтому время выполнения не более чем пропорционально 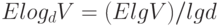 .
. 
Если E пропорционально 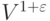 , то из леммы 20.12 следует, что время выполнения в худшем случае пропорционально
, то из леммы 20.12 следует, что время выполнения в худшем случае пропорционально  , а это значение линейно при любом значении константы
, а это значение линейно при любом значении константы 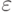 . Например, если количество ребер пропорционально V3/2, то затраты меньше 2E; если количество ребер пропорционально V4/3, то затраты меньше 3E; а если количество ребер пропорционально V5/4, то затраты не превышают 4E. Для графа с одним миллионом вершин и насыщенностью не более 10 затраты меньше 6E.
. Например, если количество ребер пропорционально V3/2, то затраты меньше 2E; если количество ребер пропорционально V4/3, то затраты меньше 3E; а если количество ребер пропорционально V5/4, то затраты не превышают 4E. Для графа с одним миллионом вершин и насыщенностью не более 10 затраты меньше 6E.
Соблазн минимизировать таким способом граничное значение времени выполнения в худшем случае упирается в понимание, что часть  никуда девать не удастся (для операции извлечь минимальное необходимо просмотреть d потомков при спуске по пирамидальному дереву), хотя часть
никуда девать не удастся (для операции извлечь минимальное необходимо просмотреть d потомков при спуске по пирамидальному дереву), хотя часть  вряд ли будет достижима (т.к. большая часть ребер не требует обновления очереди с приоритетами, как было показано при обсуждении вслед за леммой 20.8).
вряд ли будет достижима (т.к. большая часть ребер не требует обновления очереди с приоритетами, как было показано при обсуждении вслед за леммой 20.8).
Для типичных графов, наподобие задействованных в экспериментах для таблицы 20.2, уменьшение d не влияет на время выполнения, а использование больших значений d может слегка замедлить реализацию. Однако элементарная защита от худшей производительности делает целесообразной реализацию этого метода в силу ее простоты. В принципе, можно настроить реализацию так, чтобы можно было выбирать оптимальное значение d для некоторых видов графов (выбирайте наибольшее значение, которое не замедляет алгоритм), но вполне подойдет и небольшое фиксированное значение (например, 3, 4 или 5), за исключением, разве что, отдельных крупных классов графов с нетипичными характеристиками.
Если хранить стандартное бинарное пирамидально упорядоченное полное дерево в массиве (вверху), то для перехода из узла i вниз по дереву в его дочерние узлы 2i и 2i + 1 и вверх по дереву к его предку i/2 используются неявные ссылки. В 3-арном пирамидальном дереве (в центре) неявными ссылками узла i являются ссылки на дочерние узлы 3i — 1, 3i и 3i + 1 и на родительский узел  . Наконец, в 4- арном пирамид-лальном дереве (внизу) неявными ссылками узла i являются ссылки на дочерние узлы 4i — 2, 4i — 1, 4i и 4 i + 1 и на родительский узел
. Наконец, в 4- арном пирамид-лальном дереве (внизу) неявными ссылками узла i являются ссылки на дочерние узлы 4i — 2, 4i — 1, 4i и 4 i + 1 и на родительский узел  . Увеличение коэффициента ветвления в реализации неявного пирамидального дерева может оказаться полезным в приложениях, подобных алгоритму Прима, где требуется выполнение большого количества операций уменьшить ключ.
. Увеличение коэффициента ветвления в реализации неявного пирамидального дерева может оказаться полезным в приложениях, подобных алгоритму Прима, где требуется выполнение большого количества операций уменьшить ключ.
Программа 20.10. Реализация очереди с приоритетами на основе многопутевого пирамидального дерева
Этот класс использует многопутевые пирамидальные деревья для реализации косвенного интерфейса очереди с приоритетами, который используется в данной книге. В его основе лежат следующие изменения, внесенные в программу 9.12: конструктор принимает ссылку на вектор приоритетов, вместо delmax и change реализованы функции getmin и lower, и обобщены функции fixUp и fixDown, чтобы они могли поддерживать пирамидальное d-дерево. В силу последнего изменения операция извлечь минимальное выполняется за время, пропорциональное  , но операция уменьшить ключ выполняется менее чем за
, но операция уменьшить ключ выполняется менее чем за 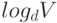 шагов.
шагов.
template <class keyType>
class PQi
{ int d, N;
vector<int> pq, qp;
const vector<keyType> &a;
void exch(int i, int j)
{ int t = pq[i]; pq[i] = pq[j]; pq[j] = t;
qp[pq[i]] = i; qp[pq[j]] = j;
}
void fixUp(int k)
{ while (k > 1 && a[pq[(k+d-2)/d]] > a[pq[k]])
{ exch(k, (k+d-2)/d); k = (k+d-2)/d; }
}
void fixDown(int k, int N)
{ int j;
while ((j = d*(k-1)+2) <= N)
{ for (int i = j+1; i < j+d && i <= N; i++)
if (a[pq[j]] > a[pq[i]]) j = i;
if (!(a[pq[k]] > a[pq[j]])) break;
exch(k, j); k = j;
}
}
public:
PQi(int N, const vector<keyType> &a, int d = 3) :
a(a), pq(N+1, 0), qp(N+1, 0), N(0), d(d) { }
int empty() const { return N == 0; }
void insert(int v)
{ pq[ + +N] = v; qp[v] = N; fixUp(N); }
int getmin()
{ exch(1, N); fixDown(1, N-1); return pq[N--]; }
void lower(int k)
{ fixUp(qp[k]); }
};
Использование пирамидальных d-деревьев неэффективно для разреженных графов, поскольку d должно быть целым числом, большим или равным 2, из чего следует, что мы не можем получить асимптотическое время выполнения меньше VlgV. Если плотность графа принимает небольшое постоянное значение, то линейный по времени алгоритм вычисления MST будет выполняться за время, пропорциональное V.
Цель разработки практических алгоритмов вычисления MST для разреженных графов за линейное время все еще не достигнута. Интенсивно изучались различные варианты алгоритма Борувки как основы для алгоритмов вычисления MST для сильно разреженных графов за почти линейное время (см. раздел ссылок). Такие исследования позволяют надеяться на получение в будущем линейного по времени алгоритма, пригодного для практических целей; было даже доказано существование рандомизированного линейного по времени алгоритма. Такие алгоритмы обычно довольно сложны, но упрощенные версии некоторых из них могут оказаться вполне работоспособными. А пока в большинстве практических ситуаций мы можем использовать рассмотренные здесь базовые алгоритмы для вычисления MST-дерева за линейное время — возможно, с дополнительным множителем lgV для некоторых разреженных графов.
Упражнения
20.71.[ В. Высоцкий] Разработайте реализацию алгоритма, описанного в разделе 20.2, который строит MST, добавляя в него ребра по одному за раз и удаляя самые длинные ребра из образующихся циклов (см. упражнение 20.33). Воспользуйтесь представлением леса MST-поддеревьев в виде родительских ссылок. Указание. При обходе путей в деревьях меняйте направления указателей на обратные.
20.72. Эмпирически сравните время выполнения реализации из упражнения 20.71 и времени выполнения алгоритма Крускала для различных видов взвешенных графах (см. упражнения 20.9—20.14). Проверьте, влияет ли на результаты рандомизация порядка просмотра ребер.
20.73. Опишите, как можно найти MST для такого большого графа, что в памяти одновременно могут находиться лишь V ребер.
20.74. Разработайте реализацию очереди с приоритетами, в которой операции извлечь минимальное и найти минимальное выполняются за постоянное время, а время выполнения операции уменьшить ключ пропорционально логарифму размера очереди с приоритетами. Сравните полученную реализацию с пирамидальными 4-деревьями, когда для вычисления MST-дерева разреженных графов используется алгоритм Прима, для различных видов взвешенных графов (см. упражнения 20.9—20.14).
20.75. Эмпирически сравните производительность различных реализаций очереди с приоритетами при использовании алгоритма Прима для различных видов взвешенных графов (см. упражнения 20.9—20.14). Рассмотрите пирамидальные d-деревья для различных значений d, биномиальные очереди, контейнер priority_queue из библиотеки STL, сбалансированные деревья и любые другие структуры данных, которые вы сочтете эффективными.
20.75. Разработайте реализацию, которая позволяет использовать в алгоритме Борувки обобщенную очередь, содержащую лес MST-поддеревьев. (Применение программы 20.9 соответствует использованию очереди FIFO.) Поэкспериментируйте с другими реализациями обобщенных очередей для различных видов взвешенных графов (см. упражнения 20.9—20.14).
20.77. Разработайте генератор случайных связных кубических графов (каждая вершина которого имеет степень 3) с ребрами случайных весов. Подстройте рассмотренные нами алгоритмы вычисления MST для этого случая, а затем определите, какой из них работает быстрее.
20.78. Для V = 106 начертите график зависимости отношения верхней границы трудоемкости алгоритма Прима с пирамидальным d-деревом к E от насыщенности d, для а из диапазона от 1 до 100.
20.79. Из таблицы 20.2 следует, что стандартная реализация алгоритма Крускала работает значительно быстрее, чем реализация с частичным упорядочением, для графов малой плотности. Объясните это явление.
20.80. Эмпирически определите в стиле таблицы 20.2 результаты для случайных полных графов с нормально распределенными весами (см. упражнение 20.18).

