Минимальные остовные деревья

Основные принципы алгоритмов построения MST -дерева

Построение MST-дерева — одна из наиболее изученных задач среди описанных в этой книге. Основные принципы ее решения были известны задолго до разработки современных структур данных и современных технологий анализа производительности алгоритмов, еще в те времена, когда поиск MST для графа, скажем, с тысячей ребер, представлял собой крайне сложную задачу. Как мы увидим, некоторые новые алгоритмы построения MST отличаются от старых главным образом способами использования и реализации алгоритмов и структур данных для основных задач, которые (наряду с мощью современных компьютеров) позволяют вычислять MST-деревья с миллионами и даже миллиардами ребер.

Одно из определяющих свойств дерева (см. "Рекурсия и деревья" ) заключается в том, что добавление в дерево любого ребра порождает уникальный цикл. Это свойство лежит в основе доказательства двух фундаментальных теорем об MST-деревьях, которые мы сейчас рассмотрим. Все описанные ниже алгоритмы основаны на этих теоремах или хотя бы одной из них.

Первая из этих теорем, которую мы далее будем называть свойством сечения, относится к идентификации ребер, которые должны входить в MST-дерево заданного графа. Однако для краткой формулировки этого свойства нам понадобятся несколько основных терминов из теории графов.

Иногда мы описываем сечение графа, просто задав множество вершин графа, при этом неявно подразумевается, что сечение содержит это множество и его дополнение. Обычно мы будем использовать такие сечения графа, когда оба множества не пусты — иначе перекрестных ребер не будет.

Если веса ребер графа различны, его MST уникально, а свойство сечения утверждает, что кратчайшее перекрестное ребро для каждого сечения должно входить в MST-дерево. При наличии равных весов может оказаться несколько минимальных секущих ребер. По крайней мере одно из них входит в состав любого заданного MST-дерева, остальные же могут входить, а могут и не входить.

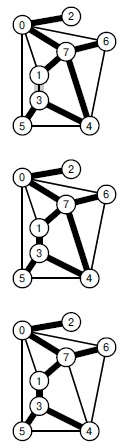
На рис. 20.5 представлены несколько примеров свойства сечения. Учтите, что минимальное ребро не обязательно должно быть единственным ребром MST, которое соединяет два множества; в случае обычных сечений существует несколько ребер, соединяющих вершину одного множества с вершиной другого. Если бы существовало лишь одно такое ребро, можно было бы разработать алгоритмы " разделяй и властвуй " на основе походящего выбора множеств, однако это не так.

Рис. 20.5. Свойство сечения

Эти четыре примера служат иллюстрацией леммы 20.1. Если вершины одного множества закрасить серым цветом, а для другого — белым, то самое короткое ребро, соединяющее серую вершину с белой, принадлежит MST-дереву.

На свойстве сечения основаны алгоритмы вычисления MST-деревьев; кроме того, оно может служить условием оптимальности, которое характеризует MST-деревья. В частности, из него следует, что каждое ребро MST-дерева есть минимальное перекрестное ребро, которое определяется вершинами двух поддеревьев, соединенных этим ребром.

Вторая теорема — свойство цикличности — применяется для выявления ребер, которые не должны входить в MST графа. То есть игнорирование этих ребер не помешает отыскать MST.

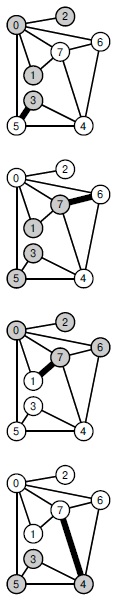
Иллюстрация свойства цикла приведена на рис. 20.6. Если взять произвольное остовное дерево, добавить в него ребро, образующее цикл, а затем удалить из этого цикла максимальное ребро, то получится остовное дерево, вес которого меньше или равен весу исходного остовного дерева. Вес нового дерева будем меньше веса исходного в том и только том случае, когда добавляемое ребро короче одного из ребер цикла.

Рис. 20.6. Свойство цикла

После добавления ребра 1-3 в граф с рис. 20.1 его MST перестает быть деревом (вверху). Чтобы найти MST нового графа, мы добавляем в MST старого графа новое ребро, которое порождает цикл (в центре). После удаления из цикла самого длинного ребра (4-7) получается MST нового графа (внизу). Один из способов проверить минимальность остовного дерева заключается в проверке, что каждое ребро, не входящее в это MST, имеет наибольший вес в цикле, который оно образует с ребрами дерева. Например, на нижней диаграмме ребро 4-6 имеет максимальный вес в цикле 4-6-7-1-3-4.

Свойство цикла лежит в основе условия оптимальности, которое характерно для MST-деревьев: из него следует, что каждое ребро любого графа, не входящее в заданное MST, является максимальным ребром цикла, который оно образует с ребрами MST.

На свойствах сечения и цикла основаны классические алгоритмы поиска MST-дерева, которые мы будем рассматривать. Мы рассматриваем ребра по одному, проверяя с помощью свойства сечения их пригодность для MST-дерева или с помощью свойства цикла — возможность их отбрасывания. Такие алгоритмы различаются по способам идентификации сечений и циклов.

Первый подход к поиску MST-дерева, который мы подробно рассмотрим — постепенное добавление ребер в MST: сначала выбираем произвольную вершину и рассматриваем ее как MST-дерево, состоящее из одной вершины, затем добавляем к нему V— 1 вершин, каждый раз выбирая минимальное ребро, которое соединяет вершину, уже включенную в MST-дерево, с вершиной, которая еще не содержится в MST. Этот метод известен как алгоритм Прима (Prim), и он будет рассмотрен в разделе 20.3.

Еще один способ вычисления MST-дерева — многократное применение свойства цикла: мы добавляем ребра по одному в заготовку MST-дерева, а если при этом образуется цикл, удаляем из него максимальное ребро (см. упражнения 20.33 и 20.71). Этот метод применяется реже, чем другие рассматриваемые нами алгоритмы — из-за трудности поддержки структуры данных, которая обеспечивает эффективную реализацию операции " удалить из цикла самое длинное ребро " .

Второй подход поиска MST-дерева, который мы подробно рассмотрим — обработка ребер в порядке возрастания их длин (вначале самые короткие) с добавлением в MST каждого ребра, которое не образует цикл с ранее включенными ребрами; процесс останавливается после добавления V— 1 ребер. Этот метод известен как алгоритм Крускала (Kruskal), который будет рассмотрен в разделе 20.4.

Третий подход к построению MST-дерева, который мы подробно изучим в разделе 20.4 — алгоритм Борувки (Boruvka). На первом шаге к MST-дереву добавляются ребра, которые соединяют каждую вершину с ее ближайшим соседом. Если веса ребер различны, этот шаг порождает лес MST-поддеревьев (мы докажем этот факт и рассмотрим усовершенствование, которое позволяет работать даже при наличии ребер с равными весами). Затем мы добавляем в MST ребра, которые соединяют каждую вершину с ее ближайшим соседом (минимальное ребро, соединяющее вершину одного дерева с вершиной другого), и повторяем этот процесс, пока не останется только одно дерево.

Рис. 20.7. Циклы в алгоритме Борувки

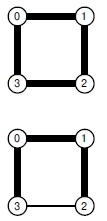
В данном графе с четырьмя вершинами все четыре ребра имеют одинаковую длину. Перед соединением каждой вершины с ближайшим соседом необходимо решить, какое ребро выбрать из множества минимальных ребер. В верхнем примере мы выбираем 1 из вершины 0, 2 из 1, 3 из 2 и 0 из 3, что приводит к образованию цикла в заготовке MST-дерева. Каждое из ребер входит в некоторое MST-дерево, но не все они входят в каждое MST. Поэтому мы используем правило разрыва связей (внизу): выбираем минимальное ребро в вершину с наименьшим индексом. Тогда из 1 мы выбираем 0, 0 из 1, 1 из 2 и 0 из 3, что и дает MST-дерево. Цикл разорван, т.к. вершина с максимальным индексом 3 не выбрана ни из одного из ее соседей (2 или 1), а она может выбрать только одного из них (0).

Все эти алгоритмы — специальные случаи общей парадигмы, которой по сей день пользуются разработчики новых алгоритмов построения MST. А именно, мы можем в произвольном порядке применять свойство сечения для выбора того или иного ребра в качестве ребра MST или свойство цикла для отбрасывания ребра и продолжать так, пока не будет возможности увеличить количество принятых или отброшенных ребер. Тогда для любого разбиения множества вершин графа на два подмножества в MST имеется соединяющее их ребро (то есть применение свойства сечения не увеличит количество ребер в MST). И все циклы графа содержат, по меньшей мере, одно ребро, не входящее в MST (то есть применение свойства цикла не увеличит количество ребер, не входящих в MST). Оба эти свойства вместе позволяют вычислить полное MST-дерево.

Точнее, все три алгоритма, которые мы рассмотрим ниже, можно свести к одному обобщенному алгоритму. Этот алгоритм начинается с выбора леса MST-поддеревьев, состоящих из одиночных вершин (и не содержащих ребер), затем выполняется шаг добавления в MST минимального ребра, соединяющего два любых поддерева леса, и эти шаги повторяются V— 1 раз, пока не останется единственное MST-дерево. Согласно свойству сечения, ни одно из ребер, порождающих цикл, не стоит рассматривать в качестве кандидата на включение в MST-дерево, поскольку ранее одно из ребер уже было минимальным ребром, пересекающим некоторое сечение между MST-поддеревьями, содержащими его вершины. В алгоритме Прима ребра добавляются по одному к единственному дереву; алгоритмы Крускала и Борувки объединяют деревья в лесе.

Согласно описанию, приведенному в этом разделе и в классической литературе, для выполнения данных алгоритмов необходимы высокоуровневые абстрактные операции, такие как:

• Отыскание минимального ребра, соединяющего два поддерева.
• Определение, будет ли образован цикл при включении указанного ребра.
• Удаление из цикла самого длинного ребра.

Наша задача заключается в разработке алгоритма и структур данных для эффективной реализации этих операций. К счастью, эта задача позволяет использовать базовые алгоритмы и структуры данных, разработанные ранее в этой книге.

Алгоритмы поиска MST-деревьев имеют долгую и интересную историю, которая еще не закончена; мы будем излагать эту историю по мере изучения конкретных алгоритмов. Развитое за много лет понимание различных методов реализации базовых абстрактных операций не позволяет объективно оценить зарождение этих алгоритмов. Вообще-то они были впервые описаны в двадцатых годах прошлого столетия — то есть до появления компьютеров в современном виде и до появления фундаментальных алгоритмов сортировки и многих других алгоритмов. Как нам теперь известно, выбор базовых алгоритмов и структур данных существенно влияет на производительность, даже при реализации простейших схем вычислений. В последние годы исследования задачи поиска MST-деревьев в основном касаются таких вопросов реализации, где используются все те же классические схемы. Для последовательности и ясности изложения мы будем называть базовые подходы по приведенным здесь именам, хотя их абстрактные версии были рассмотрены намного раньше, и современные реализации используют алгоритмы и структуры данных, разработанные намного позже этих методов.

Алгоритм построения MST-деревьев за линейное время не найден до сих пор. Как мы увидим, многие наши реализации выполняются за линейное время в большом множестве реальных ситуаций, однако в худшем случае эта зависимость уже не линейна. Разработка алгоритмов с гарантированным линейным временем выполнения на разреженных графах все еще остается недостижимой целью.

Помимо естественного поиска алгоритма решения этой фундаментальной задачи, изучение алгоритмов поиска MST подчеркивает важность понимания основных характеристик производительности фундаментальных алгоритмов. Программисты используют алгоритмы и структуры данных все более высокого уровня абстракции, и такие ситуации встречаются все чаще. Наши реализации АТД обладают различным быстродействием, и по мере использования высокоуровневых АТД в качестве компонентов алгоритмов решения задач еще более высокого уровня количество вариантов увеличивается. Алгоритмы, основанные на использовании MST и подобных им абстракций (благодаря эффективным реализациям, которые будут рассмотрены ниже в этой главе), часто используются для решения других задач на еще более высоком уровне абстракции.

Упражнения

20.26. Пронумеруйте (по порядку) от 0 до 5 следующие точки на плоскости:

(1,3) (2,1) (6,5) (3,4) (3,7) (5,3).

Принимая длину ребер в качестве их весов, приведите MST-дерево для графа, заданного множеством ребер

1-03-55-23-45-10-30-44-22-3.

20.27. Предположим, что все ребра графа имеют различные веса. Должно ли самое короткое его ребро принадлежать MST-дереву? Докажите это или приведите контрпример.

20.28. Выполните упражнение 20.27 для самого длинного ребра графа.

20.29. Приведите контрпример, демонстрирующий ошибочность следующей стратегии поиска MST: " Начните с любой вершины, считая ее MST-деревом с одной вершиной, а затем добавьте к этому дереву V— 1 вершину, всегда выбирая следующим минимальное ребро, инцидентное последней включенной в MST вершине " .

20.30. Предположим, что все ребра заданного графа имеют различные веса. Должно ли минимальное в каждом цикле ребро принадлежать MST-дереву? Докажите это утверждение или приведите контрпример.

20.31. Пусть задано MST-дерево для графа G, а затем из графа G удалено некоторое ребро. Опишите, как найти MST для нового графа за время, пропорциональное количеству ребер графа G.

20.32. Постройте MST-дерево, которое получается после многократного применения свойства цикла к графу, изображенному на рис. 20.1, если выбирать ребра в указанном порядке.

20.33. Докажите, что многократное применение свойства цикла приводит к построению MST-дерева.

20.34. Опишите, как (при необходимости) адаптировать каждый алгоритм из описанных в данном разделе для решения задачи поиска минимального остовного леса для взвешенного графа (объединение MST-деревьев его связных компонентов).