|
Здравствуйте прошла курсы на тему Алгоритмы С++. Но не пришел сертификат и не доступен.Где и как можно его скаачат? |
Специальные методы сортировки
Программа 11.2. Нечетно-четное слияние Бэтчера (рекурсивная версия)
Данная рекурсивная программа реализует абстрактное обменное слияние, используя для этой цели операции shuffle и unshuffle из программы 11.1, хотя это и не обязательно - программа 11.3 представляет собой нерекурсивную версию данной программы, в которой тасование не используется. Самое интересное здесь то, что если размер файла является степенью 2, то эта реализация является компактным описанием алгоритма Бэтчера.
template <class Item>
void merge(Item a[], int l, int m, int r)
{ if (r == l+1) compexch(a[l], a[r]);
if (r < l+2) return;
unshuffle(a, l, r);
merge(a, l, (l+m)/2, m);
merge(a, m+1, (m+1+r)/2, r);
shuffle(a, l, r);
for (int i = l+1; i < r; i += 2)
compexch(a[i], a[i+1]);
}
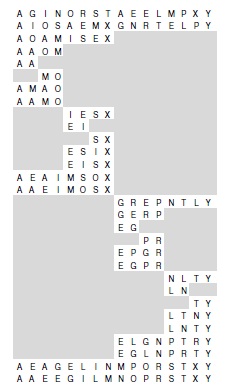
Чтобы слить ключи A G I N O R S T с ключами A E E L M P X Y, мы начинаем с выполнения операции обратного тасования, порождающей две независимые задачи слияния наполовину меньших массивов (показаны во второй строке): теперь нужно слить A I O S с A E M X (в первой половине массива) и G N R T с E L P Y (во второй половине массива). После рекурсивного решения этих подзадач мы тасуем результирующие массивы, (показаны в предпоследней строке) и завершаем сортировку выполнением операций сравнения-обмена E с A, G с E, L с I, N с M, P с O, R с S и T с X.
Почему данный метод сортирует все возможные перестановки входных данных? Ответ на этот вопрос далеко не очевиден; классическое доказательство этого факта является косвенным и зависящим от общих характеристик неадаптивных программ сортировки.
Лемма 11.1. (Принцип нулей и единиц.) Если неадаптивная программа выдает отсортированный результат для входных данных, состоящих только из 0 и 1, то она праавильно выполнит сортировку входных данных с произвольными ключами.
См. упражнение 11.7. 
Лемма 11.2. Нечетно-четное слияние Бэтчера (программа 11.2) правильно выполняет слияние.
Используя принцип нулей и единиц, достаточно проверить, правильно ли выполняются слияния, когда входными ключами являются только нули и единицы. Предположим, что в первом подфай-ле содержатся i нулей, а во втором подфайле - j нулей. Для доказательства этого свойства нужно рассмотреть четыре случая, в зависимости от того, являются ли i и j четными или нечетными числами. Если обе они четные, то одна подзадача слияния выполняется над файлом с i/2 нулями, а другая - над файлом с j/2 нулями, и вместе получается (i + j) / 2 нулей. После тасования получится сортированный файл типа 0-1.
Файл типа 0-1 также будет отсортирован после тасования и в тех случаях, когда i четно, а j нечетно, и когда i нечетно, а j четно. Но если и i, и j нечетны, то в завершение тасуется файл, содержащий (i + j) / 2 + 1 нулей, с файлом, содержащим (i + j) / 2 - 1 нулей, поэтому полученный после тасования файл содержит i + j - 1 нулей, единицу, ноль и N- i -j - 1 единиц (см.
рис.
11.3), и на завершающем этапе один из компараторов заканчивает сортировку. 
На самом деле нет необходимости тасовать данные. И действительно, программы 11.2 и 8.3 могут быть переделаны таким образом, чтобы получилась линейная сортирующая программа для любого N - для этого необходимо скорректировать реализации compexch и shuffle, чтобы они поддерживали индексы и косвенный доступ к данным (см. упражнение 11.12). Либо можно сделать так, чтобы программа генерировала последовательность команд сравнения-обмена, которую можно применить к исходному входному файлу (см. упражнение 11.13). Эти приемы можно использовать для любого неадаптивного метода сортировки, переупорядочивающего данные при помощи операций обмена, тасования или им подобных. Что касается слияния Бэтчера, то структура этого алгоритма настолько проста, что, как будет показано в разделе 11.2, для него можно непосредственно разработать восходящую реализацию.
Каждый из этих четырех примеров состоит из 5 строк: задача слияния типа 0-1; результат выполнения операции обратного тасования, порождающий две подзадачи слияния; результат рекурсивного завершения слияний; результат тасования и результат завершающих нечетно-четных сравнений. На последнем этапе обмен выполняется только если количество нулей в обоих входных файлах нечетно.
Упражнения
11.1. Приведите результат тасования и обратного тасования ключей E A S Y Q U E S T I O N.
11.2. Обобщите программу 11.1 для реализации h-путевых тасования и обратного тасования. Обеспечьте работоспособность примененной стратегии для случая, если размер файла не кратен h.
11.3. Реализуйте операции тасования и обратного тасования без использования вспомогательного массива.
11.4. Покажите, что линейная программа, которая сортирует N различных ключей, сможет отсортировать и N не обязательно различных ключей.
11.5. Покажите, как линейная программа, приведенная в тексте, сортирует каждую из шести перестановок чисел 1, 2 и 3.
11.6. Приведите пример линейной программы, которая выполняет сортировку четырех элементов.
11.7. Докажите лемму 11.1. Совет: Покажите, что если программа не способна отсортировать некоторый входной массив с произвольными ключами, то существует некоторая последовательность нулей и единиц, которую она также не может отсортировать.
11.8. Покажите, в стиле диаграммы на рис.11.2, как программа 11.2 выполняет слияние ключей A E Q S U Y E I N O S T.
11.9. Выполните упражнение 11.8 для ключей A E S Y E I N O Q S T U.
11.10. Выполните упражнение 11.8 для ключей 1 0 0 1 1 1 0 0 0 0 0 1 0 1 0 0.
11.11. Эмпирически сравните время выполнения сортировки слиянием Бэтчера с временем выполнения стандартной нисходящей сортировки слиянием (программы 8.3 и 8.2) для N = 103, 104, 105 и 106 .
11.12. Приведите такие реализации функций compexch, shuffle и unshuffle, что программы 11.2 и 8.3 будут работать в режиме косвенной сортировки (см. "Элементарные методы сортировки" ).
11.13. Приведите такие реализации функций compexch, shuffle и unshuffle, что программы 11.2 и 8.3 будут выводить для заданного N линейную программу сортировки N элементов. Для отслеживания значений индексов можно воспользоваться вспомогательным глобальным массивом.
11.14. Если переставить элементы второго сливаемого файла в обратном порядке, получится битоническая последовательность (см. определение в "Слияние и сортировка слиянием" ). После изменения заключительного цикла программы 11.2 так, чтобы он начинался с l, а не с l+1, получится программа, сортирующая битонические последовательности. Покажите, в стиле диаграммы на рис. 11.2, как с помощью этого метода выполняется слияние ключей A E S Q U Y T S O N I E.
11.15. Докажите, что модификация программы 11.2, описанная в упражнении 11.14, способна отсортировать любую битоническую последовательность.