|
Здравствуйте прошла курсы на тему Алгоритмы С++. Но не пришел сертификат и не доступен.Где и как можно его скаачат? |
Специальные методы сортировки
Реализации сортировки-слияния
Общая стратегия сортировки-слияния, описанная в разделе 11.13, доказала свою эффективность на практике. В данном разделе мы рассмотрим два усовершенствования этой стратегии, позволяющих снизить затраты. Первое из них, метод выборки с замещением (replacement selection), оказывает на время выполнения тот же эффект, что и увеличение объема используемой оперативной памяти; следующий метод, полифазное слияние (polyphase merging), дает тот же эффект, что и увеличение числа используемых устройств.
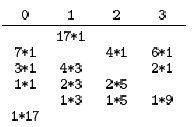
В разделе 11.3 обсуждалось применение очереди с приоритетами для P-путевого слияния, но при этом было сказано, что P настолько мало, что повышение быстродействия очереди практически ничего не дает. Однако на этапе начального распределения можно воспользоваться быстрыми очередями с приоритетами, чтобы получить отсортированные отрезки, размеры которых больше объема оперативной памяти. Идея заключается в том, чтобы пропустить (неупорядоченные) входные данные через большую очередь с приоритетами - как и раньше, выбирая из очереди с приоритетами наименьший элемент и заменяя его следующим элементом из входных данных, с одним дополнительным условием: если новый элемент меньше, чем только что выбранный из очереди, то, поскольку он может и не стать частью текущего сортируемого блока, мы помечаем его как принадлежащий следующему блоку и считаем, что он больше всех остальных элементов текущего блока. Когда помеченный элемент доходит до вершины очереди с приоритетами, мы начинаем новый блок. Работа этого метода показана на рис. 11.14.
Эта последовательность показывает, как из последовательности A S O R T I N G E X A M P L E можно получить два отрезка данных - A I N O R S T X и A E E G L M P - длиной соответственно 8 и 7, используя для этой цели сортирующее дерево размером 5.
Лемма 11.5. В случае произвольных ключей размеры отрезков данных, полученных выборкой с замещением, примерно в два раза больше размера сортирующего дерева.
Если для получения начальных отрезков воспользоваться пирамидальной сортировкой, то сначала память заполняется записями, затем они выбираются из очереди одна за одной, до опустошения сортирующего дерева. После этого память заполняется очередным пакетом записей, и этот процесс повторяется снова и снова. В среднем во время выполнения этого процесса сортирующее дерево использует только половину отведенной памяти. В противоположность этому, выборка с замещением поддерживает постоянное заполнение оперативной памяти, поэтому неудивительно, что ее эффективность в два раза выше. Полное доказательство этого свойства требует сложного анализа (см. раздел ссылок), хотя его нетрудно проверить экспериментально (см. упражнение 11.47). 
Для случайно упорядоченных файлов практический результат применения выборки с замещением состоит в возможном уменьшении числа проходов на один: вместо того, чтобы начать с отсортированных отрезков с размером, примерно равным объему оперативной памяти, мы можем начать с отрезков в два раза большего размера. Для P = 2 такая стратегия экономит точно один проход слияния, для больших значений P эффект менее заметен. Однако мы знаем, что на практике сортировка случайно упорядоченных файлов встречается редко, и при наличии некоторой упорядоченности использование выборки с замещением может дать отрезки очень больших размеров. Например, если ни одному из ключей в файле не предшествуют более M больших его ключей, то этот файл может быть полностью отсортирован во время прохода выборки с замещением, и слияние вообще не понадобится! Эта возможность служит наиболее веским аргументом в пользу практического применения выборки с замещением.
Главным недостатком сбалансированной многопутевой сортировки является то, что во время слияний активно используется лишь примерно половина внешних устройств: P входных устройств и устройство, на которое записываются выходные данные. Альтернативой этому является выполнение (2P - 1)-путевых слияний с записью на устройство 0 и с распределением данных на другие устройства после каждого прохода слияния. Но этот способ не повышает эффективность, поскольку он удваивает количество проходов распределения данных. Сбалансированное многопутевое слияние, похоже, требует либо дополнительного числа внешних устройств, либо выполнения дополнительных копирований. Разработано несколько хитроумных алгоритмов, которые обеспечивают занятость всех внешних устройств с помощью замены способа, которым сливаются небольшие отсортированные блоки. Простейший из этих методов называется полифазное слияние.
Идея, лежащая в основе полифазного слияния, заключается в неравномерном распределении упорядоченных блоков, которые получаются в результате выборки с замещением, на доступные ленты (оставляя одну ленту пустой) с последующим применением стратегии " сливать до исчерпания " (merge-until-empty): поскольку сливаемые отрезки неодинаковы по длине, одна лента закончится раньше остальных, после чего она может быть использована как выходная. То есть мы меняем ролями выходную ленту (на которой размещено некоторое количество отсортированных блоков) и исчерпанную входную ленту, и продолжаем этот процесс, пока не останется только один блок. Соответствующий пример показан на рис. 11.15.
Стратегия " сливать до исчерпания " работает для произвольного количества лент, как показано на рис. 11.16.
Вместо поддержания сбалансированного количества отрезков, как это было на рис. 11.12, здесь на стадии начального распределения на лентах размещается различное количество отрезков в соответствии с заранее определенной схемой. Затем на каждой фазе выполняются трехпутевые слияния, до завершения сортировки. В этом случае число фаз больше, чем для сбалансированного слияния, но эти фазы задействуют не все данные.
Слияние разбивается на множество фаз (не все из них выполняются для всех данных), для которых не нужно дополнительное копирование. На рис. 11.16 показано, как производится расчет отрезков для начального распределения. Количество отрезков на каждом устройстве определяется обратным подсчетом.
В примере, представленном на рис. 11.16, мы рассуждаем следующим образом: нужно закончить слияние с 1 отрезком на устройстве 0. Следовательно, перед последним слиянием устройство 0 должно быть свободным, а на устройствах 1, 2 и 3 должно быть по одному отрезку. Далее мы определяем, каким должно быть распределение отрезков до выполнения предпоследнего слияния, чтобы получить требуемое распределение. Одно из устройств 1, 2 или 3 должно быть пустым (чтобы его можно было использовать в качестве выходного для предпоследнего слияния) - пусть это будет устройство 3. То есть предпоследнее слияние сливает по одному отрезку с каждого из устройств 0, 1 и 2 и записывает результат на устройство 3. Поскольку предпоследнее слияние оставляет 0 отрезков на устройствах 0 и 1, оно должно начаться с одним отрезком на устройстве 0 и двумя отрезками на каждом из устройств 1 и 2. Аналогичные рассуждения приводят нас к заключению, что слияние, предшествующее только что рассмотренному, должно начинаться с 2, 3 и 4 отрезками на устройствах 3, 0 и 1 соответственно. Продолжая в том же духе, можно построить таблицу распределения отрезков: для получения очередного ряда выбираем из следующего за ним ряда максимальное число, заменяем его нулем и добавляем его к каждому из оставшихся чисел. Это соглашение соответствует определению в предыдущем ряду слияния максимального порядка, которое порождает текущий ряд. Такая техника работает с любым количеством устройств (не менее трех). Возникающие при этом числа являются обобщенными числами Фибоначчи, которые обладают множеством интересных свойств. Если количество отрезков не есть обобщенное число Фибоначчи, то вводятся фиктивные отрезки, которые необходимы для заполнения таблицы.
Основная трудность при реализации полифазного слияния состоит в распределении начальных отрезков (см. упражнение 11.54).
Получив распределение отрезков и рассуждая в прямом направлении, можно вычислить относительные размеры отрезков, рассчитывая их после каждого слияния. Например, первое слияние в примере на рис. 11.16 порождает 4 отрезка размером 3 единицы на устройстве 1 и оставляет 2 отрезка размером 1 на устройстве 0 и 1 отрезок размером 1 на устройстве 3 и т.д. Как и в случае сбалансированного многопутевого слияния, можно выполнить указанные операции умножения, просуммировать результаты (кроме нижней строки) и поделить на количество начальных отрезков, чтобы вычислить относительную стоимость в виде числа, кратного стоимости полного прохода по всем данным. Для простоты в расчет затрат мы включаем и фиктивные отрезки, что дает верхнюю границу истинной стоимости.
При начальном распределении для полифазного трехпутевого слияния файла, размер которого в 17 раз больше объема оперативной памяти, мы помещаем 7 отрезков на устройство 0, 4 отрезка на устройство 2 и 6 отрезков на устройство 3. Затем на первой фазе мы выполняем слияния до исчерпания устройства 2, при этом на устройстве 0 остаются 3 отрезка размером 1, на устройстве 3 - 2 отрезка размером 1, и на устройстве 1 - вновь созданные 4 отрезка размером 3. Для файла, в 15 раз большего объема оперативной памяти, мы вначале помещаем на устройство 0 два фиктивных отрезка (см. рис. 11.15). Общее количество обработанных в процессе полного слияния отрезков равно 59, т.е. на один меньше, чем в примере сбалансированного слияния (см. рис. 11.13), но при этом используется на 2устройства меньше (см. также упражнение 11.50).
Лемма 11.6. При наличии трех внешних устройств и оперативной памяти, достаточной для размещения M записей, сортировка-слияние, основанная на выборке с замещением с последующим двухпутевым полифазным слиянием, выполняет в среднем порядка 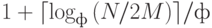 эффективных проходов.
эффективных проходов.
Общий анализ полифазного слияния, выполненный Кнутом (Knuth) и другими исследователями в шестидесятых-семидесятых годах - сложное и пространное исследование, выходящее за рамки данной книги. Для P = 3 используются числа Фибоначчи, отсюда и появление коэффициента ф. Для больших P появляются другие константы. Коэффициент 1/ф отражает тот факт, что на каждой фазе используется лишь часть данных. Мы считаем количеством " эффективных проходов " количество прочитанных данных, деленное на общее количество данных. Некоторые результаты общего анализа вызывают удивление. К примеру, оптимальный метод распределения фиктивных отрезков по устройствам использует дополнительные фазы и большее количество фиктивных отрезков, чем можно бы было предположить, поскольку некоторые отрезки используются в слияниях намного чаще других (см. раздел ссылок). 
Например, если нужно отсортировать 1 миллиард записей, используя 3 устройства и оперативную память, достаточную для размещения 1 миллиона записей, то с помощью двухпутевого полифазного слияния это можно сделать за  проходов. Добавив проход начального распределения, мы получаем несколько большие затраты (один проход), чем для сбалансированного слияния, использующего вдвое больше устройств. То есть можно считать, что полифазное слияние позволяет выполнить ту же работу, но с половиной внешних устройств. Для заданного количества устройств поли-фазное слияние всегда более эффективно, чем сбалансированное слияние, о чем свидетельствует
рис.
11.17.
проходов. Добавив проход начального распределения, мы получаем несколько большие затраты (один проход), чем для сбалансированного слияния, использующего вдвое больше устройств. То есть можно считать, что полифазное слияние позволяет выполнить ту же работу, но с половиной внешних устройств. Для заданного количества устройств поли-фазное слияние всегда более эффективно, чем сбалансированное слияние, о чем свидетельствует
рис.
11.17.
Как было сказано в начале раздела 11.3, сосредоточение нашего внимания на абстрактной машине с последовательным доступом к внешним устройствам позволило отделить вопросы, связанные с разработкой алгоритмов, от практических вопросов. При разработке практических приложений необходимо проверять, соблюдаются ли наши основные предположения. Например, мы зависим от эффективной реализации функций ввода-вывода, которые передают данные между процессором и внешними устройствами, и других системных программных средств. В современных системах такие программные средства обычно хорошо отлажены.
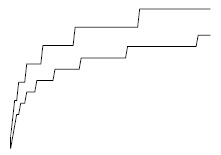
Количество проходов, выполняемых сбалансированным слиянием с 4 устройствами (вверху), всегда больше, чем количество эффективных проходов, выполняемых полифазным слиянием с 3 лентами (внизу). Представленные графики получены для функций из свойств 11.4 и 11.6, для N/M от 1 до 100. Из-за наличия фиктивных отрезков истинная производительность полифазного слияния имеет более сложный характер, чем показано данной ступенчатой функцией.
Доведя эту точку зрения до крайности, заметим, что многие современные вычислительные системы предоставляют программисту виртуальную память - более абстрактную модель доступа к внешним устройствам, чем использованная нами. В виртуальной памяти можно разместить огромное количество записей, оставив системе вопросы пересылки адресуемых данных с внешних запоминающих устройств в оперативную память; при этом доступ к данным так же удобен, как и прямой доступ к оперативной памяти. Однако эта иллюзия несовершенна: если программа обращается к участкам памяти, расположенным рядом с участками, к которым она недавно обращалась, то потребность в передаче данных с внешних устройств в оперативную память возникает нечасто, и производительность виртуальной памяти вполне удовлетворительна. (Например, в эту категорию попадают программы, осуществляющие последовательный доступ к данным.) Но если данные, к которым производится доступ, разбросаны в разных местах, то система виртуальной памяти начнет " дергаться " (thrash), т.е. тратить все время на доступ к внешним данным - с катастрофическими результатами.
Не следует игнорировать виртуальную память как возможную альтернативу для сортировки очень больших файлов. В этом случае можно непосредственно реализовать сортировку-слияние, или, еще проще, воспользоваться методом внутренней сортировки, наподобие быстрой сортировки или сортировки слиянием. Эти методы внутренней сортировки заслуживают пристального внимания в среде с хорошо реализованной виртуальной памятью. Однако такие методы, как пирамидальная сортировка или поразрядная сортировка, в которых ссылки разбросаны по памяти, скорее всего, не подойдут, т.к. система начнет дергаться.
С другой стороны, использование виртуальной памяти может привести к недопустимым затратам ресурсов, так что расчет на собственные явные методы (подобные рассмотренным выше) может оказаться наилучшим способом выжать все, на что способны высокопроизводительные внешние устройства. Одна из основных характеристик изученных выше методов заключается в том, что они разработаны так, чтобы максимально возможное количество независимых частей вычислительной системы работало с максимальной эффективностью, и ни одна из частей не простаивала. Если в качестве этих независимых частей рассматривать процессоры, мы приходим к идее параллельных вычислений - теме раздела 11.5.
Упражнения
11.45. Покажите, какие отрезки порождаются выборкой с замещением, использующей очередь с приоритетами размером 4, для ключей E A S Y Q O U E S T I O N.
11.46. Как отразится использование выборки с замещением для файла, порожденного с помощью выборки с замещением из заданного файла?
11.47. Определите эмпирически среднее число отрезков, порожденных выборкой с замещением, в которой используется очередь с приоритетами размером 1000, для случайно упорядоченных файлов размером N = 103, 104, 105 и 106 .
11.48. Каким будет количество отрезков в худшем случае при использовании выборки с замещением для генерации начальных отрезков из файла, содержащего N записей, с использованием очереди с приоритетами размером M, при M < N?
11.49. Покажите, в стиле рис. 11.15, как с помощью полифазного слияния выполняется сортировка ключей E A S Y Q U E S T I O N W I T H P L E N T Y O F K E Y S.
11.50. В примере полифазного слияния на рис. 11.15 два фиктивных отрезка были помещены на магнитную ленту с 7 отрезками. Найдите другие способы распределения фиктивных отрезков по лентам и выберите среди них такой, который обеспечивает минимальную стоимость слияния.
11.51. Составьте таблицу, соответствующую рис. 11.13, для определения максимального количества отрезков, которые могут быть слиты сбалансированным трехпутевым слиянием с пятью проходами по данным (используя шесть устройств).
11.52. Составьте таблицу, соответствующую рис. 11.16, для определения максимального количества отрезков, которые могут быть слиты полифазным слиянием с теми же затратами, что и пять проходов по всем данным (используя шесть устройств).
11.53. Напишите программу, вычисляющую количество проходов, выполняемых многопутевым слиянием, и эффективное количество проходов, выполняемых поли-фазным слиянием для заданного количества устройств и заданного количества начальных блоков. Используйте полученную программу для вывода таблицы этих затрат при работе каждого метода, для P = 3, 4, 5, 10 и 100 и N = 103, 104, 105 и 106 .
11.54. Напишите программу, последовательно назначающую начальные отрезки устройствам перед выполнением P-путевого полифазного слияния. Если количество отрезков есть обобщенное число Фибоначчи, отрезки должны быть распределены по устройствам так, как требует алгоритм; ваша задача заключается в отыскании удобного способа последовательного распределения отрезков.
11.55. Реализуйте выборку с замещением, воспользовавшись интерфейсом, определенным в упражнении 11.38.
11.56. Реализуйте сортировку-слияние, комбинируя решения упражнений 11.38 и 11.55. Используйте полученную программу для сортировки файла максимально возможного в вашей системе размера, воспользовавшись полифазным слиянием. При возможности определите, как отражается на времени выполнения программы увеличение числа устройств.
11.57. Как нужно обрабатывать небольшие файлы в реализации быстрой сортировки при упорядочении очень большого файла в среде с виртуальной памятью?
11.58. Если на вашем компьютере функционирует подходящая система виртуальной памяти, выполните эмпирическое сравнение быстрой сортировки, LSD-сортировки, MSD-сортировки и пирамидальной сортировки для очень больших файлов. Используйте размер файла, максимально возможный в вашей системе.
11.59. Разработайте реализацию рекурсивной многопутевой сортировки слиянием, основанной на k-путевом слиянии, которую можно использовать для сортировки очень больших файлов в среде с виртуальной памятью (см. упражнение 8.11).
11.60. Если на вашем компьютере функционирует подходящая система виртуальной памяти, эмпирически определите значение к, при котором достигается минимальное время выполнения реализации из упражнения 11.59. Используйте размер файла, максимально возможный в вашей системе.